Fractional Fourier Transform and Distributions in the Ray Space: Application for the Analysis of Radio Occultation Data
Abstract
:1. Introduction
2. Algorithm Description
2.1. Quasiprobability Distribution Functions
2.2. Phase Space Scaling
2.3. Phase Space Rotation
3. Numerical Implementation
3.1. Discretization
3.2. Fractional Fourier Transform
- Determination of K and evaluation of . For , the standard fast Fourier transform (FFT) is employed;
- Evaluation of ;
- Evaluation of , where . The standard FFT is employed. This function is obtained for the standard grid , where the corresponding grid of y is ;
- Interpolation of from the grid to the standard grid , producing ;
- Final evaluation of .
3.3. Kirkwood Distribution Function and Its Averaging over Rotations
3.4. Wigner Distribution Function
4. Tests with Simple Signals
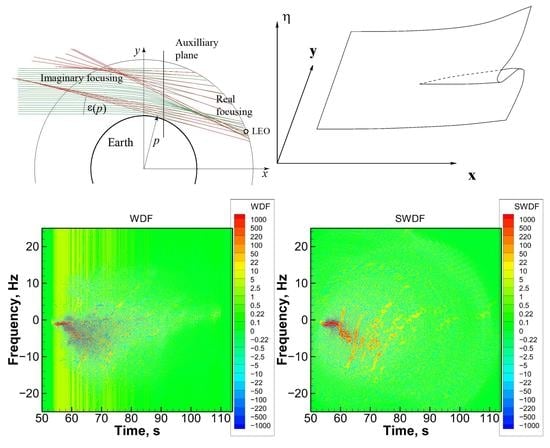
5. Results of Processing RO Data
6. Discussion
- It effectively suppresses the “quantum oscillations”, which are imminent to the WDF.
- Its resolution is good enough for practical purposes.
- It has no preferred direction in the phase space because it is invariant with respect to the phase space rotation.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FIO | Fourier Integral Operators |
| FFT | Fast Fourier Transform |
| FrFT | Fractional Fourier Transform |
| GNSS | Global Navigation Satellite Systems |
| GO | Geometrical Optics |
| KDF | Kirkwood Distribution Function |
| RH | Radio Holography |
| RO | Radio Occultation |
| SWDF | Smoothed Wigner Distribution Function |
| WDF | Wigner Distribution Function |
| WO | Wave Optics |
References
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate and space weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef] [Green Version]
- Pavelyev, A.G. On the Feasibility of Radioholographic Investigations of Wave Fields Near the Earth’s Radio-Shadow Zone on the Satellite-to-Satellite Path. J. Commun. Technol. Electron. 1998, 43, 875–879. [Google Scholar]
- Mortensen, M.D.; Høeg, P. Inversion of GPS occultation measurements using Fresnel diffraction theory. Geophys. Res. Lett. 1998, 25, 2441–2444. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Gurvich, A.S. Algorithms of inversion of Microlab-1 satellite data including effects of multipath propagation. Int. J. Remote Sens. 1998, 19, 2283–2300. [Google Scholar] [CrossRef]
- Mortensen, M.D.; Linfield, R.P.; Kursinski, E.R. Vertical resolution approaching 100 m for GPS occultations of the Earth’s atmosphere. Radio Sci. 1999, 36, 1475–1484. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Gurvich, A.S.; Kornblueh, L. Comparative analysis of radioholographic methods of processing radio occultation data. Radio Sci. 2000, 35, 1025–1034. [Google Scholar] [CrossRef]
- Høeg, P.; Jensen, A.S.; Nielsen, A.S.; Lohmann, M.; Schroder, T.M.; Grove-Rasmussen, J.; Larsen, G.B. Radio Occultation Signal Analysis; ACE-Scientific Support Study WP6300(1); Atmosphere Ionosphere Research Division, Danish Meteorological Institute: Copenhagen, Denmark, 2001.
- Beyerle, G.; Hocke, K. Observation and simulation of direct and reflected GPS signals in radio occultation experiments. Geophys. Res. Lett. 2001, 28, 1895–1898. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radioholographic Methods for Processing Radio Occultation Data in Multipath Regions; Scientific Report 01-02; Danish Meteorological Institute: Copenhagen, Denmark, 2001.
- Gorbunov, M.E.; Kornblueh, L. Analysis and validation of GPS/MET radio occultation data. J. Geophys. Res. 2001, 106, 17161–17169. [Google Scholar] [CrossRef]
- Beyerle, G.; Hocke, K.; Wickert, J.; Schmidt, T.; Marquardt, C.; Reigber, C. GPS radio occultations with CHAMP: A radio holographic analysis of GPS signal propagation in the troposphere and surface reflections. J. Geophys. Res. 2002, 107, 4802. [Google Scholar] [CrossRef] [Green Version]
- Jensen, A.S.; Benzon, H.H.; Lohmann, M.S. A New High Resolution Method for Processing Radio Occultation Data; Scientific Report 02-06; Danish Meteorological Institute: Copenhagen, Denmark, 2002.
- Gorbunov, M.E.; Gurvich, A.S.; Shmakov, A.V. Back-propagation and radio-holographic methods for investigation of sporadic ionospheric E-layers from Microlab-1 data. Int. J. Remote Sens. 2002, 23, 675–685. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Canonical transform method for processing radio occultation data in the lower troposphere. Radio Sci. 2002, 37, 9-1–9-10. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radio-holographic analysis of Microlab-1 radio occultation data in the lower troposphere. J. Geophys. Res. 2002, 107, 7-1–7-10. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radioholographic analysis of radio occultation data in multipath zones. Radio Sci. 2002, 37, 14-1–14-9. [Google Scholar] [CrossRef] [Green Version]
- Pavelyev, A.; Igarashi, K.; Reigber, C.; Hocke, K.; Wickert, J.; Beyerle, G.; Matyugov, S.; Kucherjavenkov, A.; Pavelyev, D.; Yakovlev, O. First application of the radioholographic method to wave observations in the upper atmosphere. Radio Sci. 2002, 37, 1043. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Benzon, H.H.; Nielsen, A.S. Full spectrum inversion of radio occultation signals. Radio Sci. 2003, 38, 1040. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kornblueh, L. Analysis and validation of Challenging Minisatellite Payload (CHAMP) radio occultation data. J. Geophys. Res. 2003, 108, 4584. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S.; Benzon, H.H. Geometrical optics phase matching of radio occultation signals. Radio Sci. 2004, 39, RS3009. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Benzon, H.H.; Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S. Comparative analysis of radio occultation processing approaches based on Fourier integral operators. Radio Sci. 2004, 39, RS6004. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and its application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Wave Optics Algorithms for Processing Radio Occultation Data in the Lower Troposphere: A Review and Synthesis. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; pp. 11–24. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Canonical Transform Methods for Radio Occultation Data. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; pp. 61–68. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Radio Holographic Filtering of Noisy Radio Occultations; Scientific Report 05-06; Danish Meteorological Institute: Copenhagen, Denmark, 2005. Available online: https://www.dmi.dk/fileadmin/Rapporter/SR/sr05-06.pdf (accessed on 29 September 2022).
- Gorbunov, M.E.; Lauritsen, K.B.; Rodin, A.; Tomassini, M.; Kornblueh, L. Analysis of the CHAMP experimental data on radio-occultation sounding of the Earth’s atmosphere. Izv. Atm. Ocean. Phys. 2005, 41, 726–740. [Google Scholar]
- Jensen, A.S.; Benzon, H.H.; Lohmann, M.S.; Nielsen, A.S. Processing radio occultation data by full spectrum inversion techniques: An overview and recent developments. In Atmosphere and Climate, Studies by Radio Occultation Methods; Foelsche, U., Kirchengast, G., Steiner, A., Eds.; Springer: New York, NY, USA, 2006; pp. 96–112. [Google Scholar]
- Gorbunov, M.E.; Lauritsen, K.B.; Leroy, S.S. Application of Wigner distribution function for analysis of radio occultations. Radio Sci. 2010, 45, RS6011. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B.; Leroy, S.S. Analysis of RO data retrieved from the Wigner distribution function. In Proceedings of the International Radio Occultation Working Group, 2nd Workshop, Estes Park, CO, USA, 28 March–3 April 2012. [Google Scholar]
- Pavelyev, A.G.; Liou, Y.A.; Matyugov, S.S.; Pavelyev, A.A.; Gubenko, V.N.; Zhang, K.; Kuleshov, Y. Application of the locality principle to radio occultation studies of the Earth’s atmosphere and ionosphere. Atmos. Meas. Tech. 2015, 8, 2885–2899. [Google Scholar] [CrossRef] [Green Version]
- Sievert, T.; Rasch, J.; Carlström, A.; Pettersson, M.I. Analysis of reflections in GNSS radio occultation measurements using the phase matching amplitude. Atmos. Meas. Tech. 2018, 11, 569–580. [Google Scholar] [CrossRef] [Green Version]
- Koval, O.A.; Gorbunov, M.E. The theory of fluctuations of radio occultation signals: Geometric optical approximation of the Canonical Transform Method. In Proceedings of the IGL-1 2018: First International Workshop on Innovating GNSS and LEO Occultations & Reflections for Weather, Climate and Space Weather, Beijing, China, 6–11 September 2018; p. 87. [Google Scholar]
- Gorbunov, M.E.; Cardellach, E.; Lauritsen, K.B. Reflected ray retrieval from radio occultation data using radio holographic filtering of wave fields in ray space. Atmos. Meas. Tech. 2018, 11, 1181–1191. [Google Scholar] [CrossRef] [Green Version]
- Koval, O.A.; Gorbunov, M.E.; Kan, V. The fluctuation theory of radio occultation signals: Geometric optical approximation of the Canonical Transform method. IOP Conf. Ser. Earth Environ. Sci. 2019, 231, 012029. [Google Scholar] [CrossRef]
- Sievert, T.; Rasch, J.; Carlström, A.; Barbosa, V.L.; Pettersson, M.I.; Vu, V. Using A Sliding Window Phase Matching Method for Imaging of GNSS Radio Occultation Signals. Remote Sens. 2021, 13, 970. [Google Scholar] [CrossRef]
- Gorbunov, M.; Kirchengast, G.; Lauritsen, K.B. Generalized canonical transform method for radio occultation sounding with improved retrieval in the presence of horizontal gradients. Atmos. Meas. Tech. 2021, 14, 853–867. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Sokolovskiy, S.V. Remote Sensing of Refractivity from Space for Global Observations of Atmospheric Parameters; Report 119; Max-Planck Institute for Meteorology: Hamburg, Germany, 1993; 58p. [Google Scholar]
- Gorbunov, M.E.; Gurvich, A.S. Microlab-1 experiment: Multipath effects in the lower troposphere. J. Geophys. Res. 1998, 103, 13819–13826. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Error Estimate of Bending Angles in the Presence of Strong Horizontal Gradients. In New Horizons in Occultation Research; Steiner, A., Pirscher, B., Foelsche, U., Kirchengast, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 17–26. [Google Scholar] [CrossRef]
- Healy, S.B. Radio occultation bending angle and impact parameter errors caused by horizontal refractive index gradients in the troposphere: A simulation study. J. Geophys. Res. 2001, 106, 11875–11890. [Google Scholar] [CrossRef]
- Zou, X.; Liu, H.; Kuo, Y.H. Occurrence and detection of impact multipath simulations of bending angle. Quart. J. R. Meteor. Soc. 2019, 145, 1690–1704. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions—A review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef] [Green Version]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Proc. Camb. Philos. Soc. 1930, 26, 376–395. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W. Über Die Inkohärente Streuung Von Röntgenstrahlen. Physik. Zeitschr. 1931, 32, 737–740. [Google Scholar]
- Wigner, E.P. On the Quantum Correction for Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Ville, J. Théorie et Applications de la Notion de Signal Analytique. Cables Transm. 1948, 2, 61–74. [Google Scholar]
- Kirkwood, J.G. Quantum statistics of almost classical assemblies. Phys. Rev. 1933, 44, 31–37. [Google Scholar] [CrossRef]
- Gorbunov, M.; Koval, O.; Kirchengast, G. Kirkwood Distribution Function and its Application for the Analysis of Radio Occultation Observations. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Gorbunov, M.E.; Koval, O.A. Kirkwood and Wigner Quantum Densities, Their Properties, and Applications in Radiophysics. Radiophys. Quantum Electron. 2021, 64, 140–148. [Google Scholar] [CrossRef]
- Mello, P.A.; Revzen, M. Wigner function and the successive measurement of position and momentum. Phys. Rev. A 2014, 89, 012106. [Google Scholar] [CrossRef] [Green Version]
- Condon, E.U. Immersion of the Fourier Transform in a Continuous Group of Functional Transformations. Proc. Natl. Acad. Sci. USA 1937, 23, 158–164. [Google Scholar] [CrossRef] [Green Version]
- Anaya-Contreras, J.; Zúñiga-Segundo, A.; Moya-Cessa, H. Quasiprobability Distribution Functions from Fractional Fourier Transforms. Symmetry 2019, 11, 344. [Google Scholar] [CrossRef] [Green Version]
- Marinho, F.J.; Bernardo, L.M. Numerical calculation of fractional Fourier transforms with a single fast-Fourier-transform algorithm. J. Opt. Soc. Am. A 1998, 15, 2111. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Modeling and inverting radio occultation signals in the moist troposphere. Radio Sci. 2001, 36, 441–458. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.V. Tracking tropospheric radio occultation signals from low Earth orbit. Radio Sci. 2001, 36, 483–498. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.; Schreiner, W.; Zeng, Z.; Hunt, D.; Lin, Y.C.; Kuo, Y.H. Observation, analysis, and modeling of deep radio occultation signals: Effects of tropospheric ducts and interfering signals. Radio Sci. 2014, 49, 954–970. [Google Scholar] [CrossRef]
- Hordyniec, P.; Kuleshov, Y.; Choy, S.; Norman, R. Observation of Deep Occultation Signals in Tropical Cyclones With COSMIC-2 Measurements. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]













| K | |
|---|---|
| 0 | unity operator |
| 1 | forward Fourier transform |
| inverse Fourier transform | |
| 2 | coordinate reversion |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorbunov, M.; Dolovova, O. Fractional Fourier Transform and Distributions in the Ray Space: Application for the Analysis of Radio Occultation Data. Remote Sens. 2022, 14, 5802. https://doi.org/10.3390/rs14225802
Gorbunov M, Dolovova O. Fractional Fourier Transform and Distributions in the Ray Space: Application for the Analysis of Radio Occultation Data. Remote Sensing. 2022; 14(22):5802. https://doi.org/10.3390/rs14225802
Chicago/Turabian StyleGorbunov, Michael, and Oksana Dolovova. 2022. "Fractional Fourier Transform and Distributions in the Ray Space: Application for the Analysis of Radio Occultation Data" Remote Sensing 14, no. 22: 5802. https://doi.org/10.3390/rs14225802