Numerical Optimization Reviews
Share This Topical Collection
Editor
 Prof. Dr. Oliver Schütze
Prof. Dr. Oliver Schütze
 Prof. Dr. Oliver Schütze
Prof. Dr. Oliver Schütze
E-Mail
Website
Collection Editor
Depto de Computacion, CINVESTAV, Mexico City 07360, Mexico
Interests: multi-objective optimization; evolutionary computation (genetic algorithms and evolution strategies); numerical analysis; engineering applications
Special Issues, Collections and Topics in MDPI journals
Topical Collection Information
Dear Colleagues,
Numerical Optimization is pivotal for decision-making in our increasingly complex world. It has numerous applications in Engineering, Finance, and Machine Learning.
This collection aims to gather review articles devoted to important disciplines in Numerical Optimization. The topics of interest include, but are not limited to, surveys on optimization algorithms for treating specific problem classes, classical mathematical programming, evolutionary computation, direct search methods, and applications of Numerical Optimization in certain fields.
Prof. Dr. Oliver Schütze
Collection Editor
Manuscript Submission Information
Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. All submissions that pass pre-check are peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on the collection website. Research articles, review articles as well as short communications are invited. For planned papers, a title and short abstract (about 100 words) can be sent to the Editorial Office for announcement on this website.
Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are thoroughly refereed through a single-blind peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Mathematical and Computational Applications is an international peer-reviewed open access semimonthly journal published by MDPI.
Please visit the Instructions for Authors page before submitting a manuscript.
The Article Processing Charge (APC) for publication in this open access journal is 1400 CHF (Swiss Francs).
Submitted papers should be well formatted and use good English. Authors may use MDPI's
English editing service prior to publication or during author revisions.
Keywords
- optimization algorithms
- mathematical programming
- evolutionary computation
- direct search methods
Published Papers (3 papers)
Open AccessFeature PaperReview
MCDM, EMO and Hybrid Approaches: Tutorial and Review
by
Ankur Sinha and Jyrki Wallenius
Cited by 1 | Viewed by 1909
Abstract
Most of the practical applications that require optimization often involve multiple objectives. These objectives, when conflicting in nature, pose both optimization as well as decision-making challenges. An optimization procedure for such a multi-objective problem requires computing (computer-based search) and decision making to identify
[...] Read more.
Most of the practical applications that require optimization often involve multiple objectives. These objectives, when conflicting in nature, pose both optimization as well as decision-making challenges. An optimization procedure for such a multi-objective problem requires computing (computer-based search) and decision making to identify the most preferred solution. Researchers and practitioners working in various domains have integrated computing and decision-making tasks in several ways, giving rise to a variety of algorithms to handle multi-objective optimization problems. For instance, an
a priori approach requires formulating (or eliciting) a decision maker’s value function and then performing a one-shot optimization of the value function, whereas an
a posteriori decision-making approach requires a large number of diverse Pareto-optimal solutions to be available before a final decision is made. Alternatively, an
interactive approach involves interactions with the decision maker to guide the search towards better solutions (or the most preferred solution). In our tutorial and survey paper, we first review the fundamental concepts of multi-objective optimization. Second, we discuss the classic interactive approaches from the field of Multi-Criteria Decision Making (MCDM), followed by the underlying idea and methods in the field of Evolutionary Multi-Objective Optimization (EMO). Third, we consider several promising MCDM and EMO hybrid approaches that aim to capitalize on the strengths of the two domains. We conclude with discussions on important behavioral considerations related to the use of such approaches and future work.
Full article
►▼
Show Figures
Open AccessFeature PaperEditor’s ChoiceReview
Surrogate Modeling Approaches for Multiobjective Optimization: Methods, Taxonomy, and Results
by
Kalyanmoy Deb, Proteek Chandan Roy and Rayan Hussein
Cited by 21 | Viewed by 3896
Abstract
Most practical optimization problems are comprised of multiple conflicting objectives and constraints which involve time-consuming simulations. Construction of metamodels of objectives and constraints from a few high-fidelity solutions and a subsequent optimization of metamodels to find in-fill solutions in an iterative manner remain
[...] Read more.
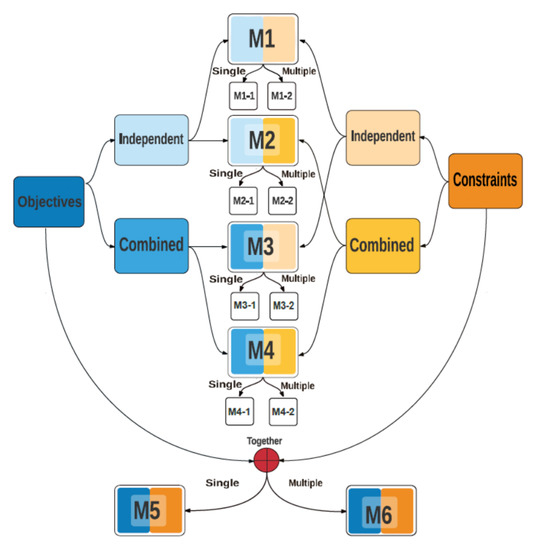
Most practical optimization problems are comprised of multiple conflicting objectives and constraints which involve time-consuming simulations. Construction of metamodels of objectives and constraints from a few high-fidelity solutions and a subsequent optimization of metamodels to find in-fill solutions in an iterative manner remain a common metamodeling based optimization strategy. The authors have previously proposed a taxonomy of 10 different metamodeling frameworks for multiobjective optimization problems, each of which constructs metamodels of objectives and constraints independently or in an aggregated manner. Of the 10 frameworks, five follow a generative approach in which a single Pareto-optimal solution is found at a time and other five frameworks were proposed to find multiple Pareto-optimal solutions simultaneously. Of the 10 frameworks, two frameworks (M3-2 and M4-2) are detailed here for the first time involving multimodal optimization methods. In this paper, we also propose an adaptive switching based metamodeling (ASM) approach by switching among all 10 frameworks in successive epochs using a statistical comparison of metamodeling accuracy of all 10 frameworks. On 18 problems from three to five objectives, the ASM approach performs better than the individual frameworks alone. Finally, the ASM approach is compared with three other recently proposed multiobjective metamodeling methods and superior performance of the ASM approach is observed. With growing interest in metamodeling approaches for multiobjective optimization, this paper evaluates existing strategies and proposes a viable adaptive strategy by portraying importance of using an ensemble of metamodeling frameworks for a more reliable multiobjective optimization for a limited budget of solution evaluations.
Full article
►▼
Show Figures
Open AccessFeature PaperReview
A Survey of Recent Trends in Multiobjective Optimal Control—Surrogate Models, Feedback Control and Objective Reduction
by
Sebastian Peitz and Michael Dellnitz
Cited by 59 | Viewed by 9130
Abstract
Multiobjective optimization plays an increasingly important role in modern applications, where several criteria are often of equal importance. The task in multiobjective optimization and multiobjective optimal control is therefore to compute the set of optimal compromises (the Pareto set) between the conflicting objectives.
[...] Read more.
Multiobjective optimization plays an increasingly important role in modern applications, where several criteria are often of equal importance. The task in multiobjective optimization and multiobjective optimal control is therefore to compute the set of optimal compromises (the Pareto set) between the conflicting objectives. The advances in algorithms and the increasing interest in Pareto-optimal solutions have led to a wide range of new applications related to optimal and feedback control, which results in new challenges such as expensive models or real-time applicability. Since the Pareto set generally consists of an infinite number of solutions, the computational effort can quickly become challenging, which is particularly problematic when the objectives are costly to evaluate or when a solution has to be presented very quickly. This article gives an overview of recent developments in accelerating multiobjective optimal control for complex problems where either PDE constraints are present or where a feedback behavior has to be achieved. In the first case, surrogate models yield significant speed-ups. Besides classical meta-modeling techniques for multiobjective optimization, a promising alternative for control problems is to introduce a surrogate model for the system dynamics. In the case of real-time requirements, various promising model predictive control approaches have been proposed, using either fast online solvers or offline-online decomposition. We also briefly comment on dimension reduction in many-objective optimization problems as another technique for reducing the numerical effort.
Full article
►▼
Show Figures