Morphology of Anisotropic Banded Structures in an Emulsion under Simple Shear
Abstract
:1. Introduction
2. Materials and Methods
3. Results
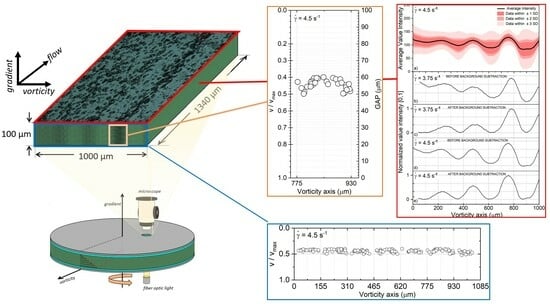
3.1. The Horizontal Distribution of Drops (Vorticity–Flow Plane)
3.2. The Vertical Distribution of Drops (Vorticity–Gradient Plane)
4. Discussion of Results
Critical Capillary in Banding
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ciamarra, M.; Coniglio, A.; Nicodemi, M. Shear instabilities in granular mixtures. Phys. Rev. Lett. 2005, 94, 188001. [Google Scholar] [CrossRef] [PubMed]
- Vermant, J.; Solomon, M.J. Flow-induced structure in colloidal suspensions. J. Phys. Condens. Matter 2005, 17, R187. [Google Scholar] [CrossRef]
- Highgate, D. Particle migration in cone-plate viscometry of suspensions. Nature 1966, 211, 1390. [Google Scholar] [CrossRef]
- Mao, C.; Huang, Y.; Qiao, Y.; Zhang, J.; Kong, M.; Yang, Q.; Li, G. Vorticity-Aligned Droplet Bands in Sheared Immiscible Polymer Blends Induced by Solid Particles. Langmuir 2020, 36, 4383–4395. [Google Scholar] [CrossRef] [PubMed]
- Wychowaniec, J.K.; Iliut, M.; Borek, B.; Muryn, C.; Mykhaylyk, O.O.; Edmondson, S.; Vijayaraghavan, A. Elastic flow instabilities and macroscopic textures in graphene oxide lyotropic liquid crystals. NPJ 2D Mater. Appl. 2021, 5, 1–10. [Google Scholar] [CrossRef]
- Van Der Gucht, J.; Lemmers, M.; Knoben, W.; Besseling, N.; Lettinga, M. Multiple shear-banding transitions in a supramolecular polymer solution. Phys. Rev. Lett. 2006, 97, 108301. [Google Scholar] [CrossRef]
- Lerouge, S.; Berret, J.-F. Shear-Induced Transitions and Instabilities in Surfactant Wormlike Micelles. In Polymer Characterization: Rheology, Laser Interferometry, Electrooptics; Dusek, K., Joanny, J.-F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–71. [Google Scholar]
- Caiazza, C.; Preziosi, V.; Tomaiuolo, G.; O’Sullivan, D.; Guida, V.; Guido, S. Flow-induced concentration gradients in shear-banding of branched wormlike micellar solutions. J. Colloid Interface Sci. 2019, 534, 695–703. [Google Scholar] [CrossRef]
- Olmsted, P.; Lu, D.; Null, C. Phase coexistence of complex fluids in shear flow. Faraday Discuss. 1999, 112, 183–194. [Google Scholar] [CrossRef]
- Olmsted, P.D. Perspectives on shear banding in complex fluids. Rheol. Acta 2008, 47, 283–300. [Google Scholar] [CrossRef]
- Fielding, S. Complex dynamics of shear banded flows. Soft Matter 2007, 3, 1262–1279. [Google Scholar] [CrossRef]
- Amis, E.; Fanconi, B. Polymers Division 2000 Programs and Accomplishments; NIST Interagency/Internal Report (NISTIR); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Migler, K. String formation in sheared polymer blends: Coalescence, breakup, and finite size effects. Phys. Rev. Lett. 2001, 86, 1023. [Google Scholar] [CrossRef]
- Salmon, J.; Manneville, C.; Molino, S.; Null, F. Velocity profiles in shear-banding wormlike micelles. Phys. Rev. Lett. 2003, 90, 228303. [Google Scholar] [CrossRef]
- Simeone, M.; Sibillo, V.; Tassieri, M.; Guido, S. Shear-induced clustering of gelling droplets in aqueous biphasic mixtures of gelatin and dextran. J. Rheol. 2002, 46, 1263–1278. [Google Scholar] [CrossRef]
- Montesi, A.; Peña, A.; Pasquali, M. Vorticity alignment and negative normal stresses in sheared attractive emulsions. Phys. Rev. Lett. 2004, 92, 58303. [Google Scholar] [CrossRef] [PubMed]
- Divoux, T.; Fardin, M.A.; Manneville, S.; Lerouge, S. Shear banding of complex fluids. Annu. Rev. Fluid Mech. 2016, 48, 81–103. [Google Scholar] [CrossRef]
- Briole, A.; Casanellas, L.; Fardin, M.-A.; Py, C.; Cardoso, O.; Browaeys, J.; Lerouge, S. Shear-banding fluid (s) under time-dependent shear flows. Part II A Test of the Moorcroft–Fielding Criteria. J. Rheol. 2021, 65, 1201–1217. [Google Scholar] [CrossRef]
- Osuji, C.; Weitz, D. Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system. Soft Matter 2008, 4, 1388–1392. [Google Scholar] [CrossRef] [PubMed]
- Schall, P.; Van Hecke, M. Shear bands in matter with granularity. Annu. Rev. Fluid Mech. 2010, 42, 67–88. [Google Scholar] [CrossRef]
- Caserta, S.; Guido, S. Vorticity Banding in Biphasic Polymer Blends. Langmuir 2012, 28, 16254–16262. [Google Scholar] [CrossRef]
- Pathak, J.; Davis, M.; Hudson, S.; Migler, K. Layered droplet microstructures in sheared emulsions: Finite-size effects. J. Colloid Interface Sci. 2002, 255, 391–402. [Google Scholar] [CrossRef]
- Lee, L.L.; Niknafs, N.; Hancocks, R.D.; Norton, I.T. Emulsification: Mechanistic understanding. Trends Food Sci. Technol. 2013, 31, 72–78. [Google Scholar] [CrossRef]
- Schuch, A.; Leal, L.G.; Schuchmann, H.P. Production of W/O/W double emulsions. Part I: Visual observation of deformation and breakup of double emulsion drops and coalescence of the inner droplets. Colloids Surf. A Physicochem. Eng. Asp. 2014, 461, 336–343. [Google Scholar] [CrossRef]
- Grace, H. Dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- De Bruijn, R. Tipstreaming of drops in simple shear flows. Chem. Eng. Sci. 1993, 48, 277–284. [Google Scholar] [CrossRef]
- Bentley, B.; Leal, L. An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 1986, 167, 241–283. [Google Scholar] [CrossRef]
- Jansen, K.; Agterof, W.; Mellema, J. Droplet breakup in concentrated emulsions. J. Rheol. 2001, 45, 227–263. [Google Scholar] [CrossRef]
- Karam, H.; Bellinger, J. Deformation and breakup of liquid droplets in a simple shear field. Ind. Eng. Chem. Fundam. 1968, 7, 576–581. [Google Scholar] [CrossRef]
- Leiva, J.M.; Geffroy, E. Evolution of the size distribution of an emulsion under a simple shear flow. Fluids 2018, 3, 46. [Google Scholar] [CrossRef]
- Luciani, A.; Champagne, M.F.; Utracki, L.A. Interfacial tension coefficient from the retraction of ellipsoidal drops. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 1393–1403. [Google Scholar] [CrossRef]
- Derkach, S.R. Rheology of emulsions. Adv. Colloid Interface Sci. 2009, 151, 1–23. [Google Scholar] [CrossRef]
- Vananroye, A.; Van Puyvelde, P.; Moldenaers, P. Effect of confinement on droplet breakup in sheared emulsions. Langmuir 2006, 22, 3972–3976. [Google Scholar] [CrossRef]
- Sundararaj, U.; Macosko, C. Drop breakup and coalescence in polymer blends: The effects of concentration and compatibilization. Macromolecules 1995, 28, 2647–2657. [Google Scholar] [CrossRef]
- Taylor, G. The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. A 1932, 138, 41–49. [Google Scholar]
- Taylor, G. The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 1934, 146, 501–524. [Google Scholar]
- Pathak, J.; Migler, K. Droplet–String Deformation and Stability during Microconfined Shear Flow. Langmuir 2003, 19, 8667–8674. [Google Scholar] [CrossRef]
- Mckinley, G.; Öztekin, A.; Byars, J.; Brown, R. Self-similar spiral instabilities in elastic flows between a cone and a plate. J. Fluid Mech. 1995, 285, 123–164. [Google Scholar] [CrossRef]
- Byars, J.; Öztekin, A.; Brown, R.; Mckinley, G. Spiral instabilities in the flow of highly elastic fluids between rotating parallel disks. J. Fluid Mech. 1994, 271, 173–218. [Google Scholar] [CrossRef]
- Choi, S.; Schowalter, W. Rheological properties of nondilute suspensions of deformable particles. Phys. Fluids 1975, 18, 420–427. [Google Scholar] [CrossRef]
- Caserta, S.; Simeone, M.; Guido, S. Shear banding in biphasic liquid-liquid systems. Phys. Rev. Lett. 2008, 100, 137801. [Google Scholar] [CrossRef]
- Wilkins, G.; Olmsted, P. Vorticity banding during the lamellar-to-onion transition in a lyotropic surfactant solution in shear flow. Eur. Phys. J. E 2006, 21, 133. [Google Scholar] [CrossRef]







| Shear Rate (s−1) | Total Number Drops | Velocity Mean (µm/s) | Standard Derivation of Velocity (µm/s) | Realtive Deviation of Velocity |
|---|---|---|---|---|
| 0.75 | 127 | 34.24 | 1.40 | 0.04 |
| 1.50 | 143 | 72.55 | 2.60 | 0.04 |
| 2.25 | 140 | 114.40 | 6.35 | 0.06 |
| 3.00 | 175 | 134.09 | 8.74 | 0.07 |
| 3.75 | 105 | 165.23 | 16.25 | 0.10 |
| 4.50 | 198 | 183.52 | 15.98 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateus, J.E.L.; Huesca, M.A.R.; Lavielle, F.M.; Aguilar, E.G. Morphology of Anisotropic Banded Structures in an Emulsion under Simple Shear. Fluids 2023, 8, 240. https://doi.org/10.3390/fluids8090240
Mateus JEL, Huesca MAR, Lavielle FM, Aguilar EG. Morphology of Anisotropic Banded Structures in an Emulsion under Simple Shear. Fluids. 2023; 8(9):240. https://doi.org/10.3390/fluids8090240
Chicago/Turabian StyleMateus, Jairo Eduardo Leiva, Marco Antonio Reyes Huesca, Federico Méndez Lavielle, and Enrique Geffroy Aguilar. 2023. "Morphology of Anisotropic Banded Structures in an Emulsion under Simple Shear" Fluids 8, no. 9: 240. https://doi.org/10.3390/fluids8090240