On the Prediction of Boundary Layer Quantities at High Reynolds Numbers
Abstract
:1. Introduction
2. Method
3. Results and Discussion
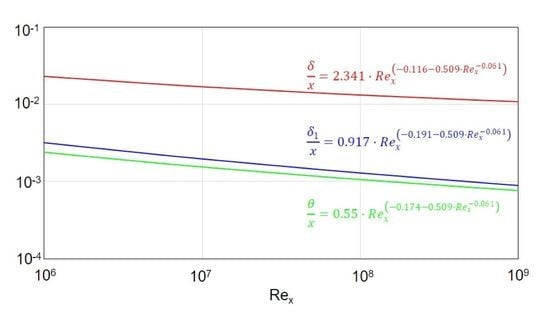
3.1. Boundary Layer Thickness
3.2. Friction Coefficients
3.3. Boundary Layer Profiles
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Tschepe, J.; Maaß, J.-T.; Nayeri, C.N.; Paschereit, C.O. Experimental investigation of the aerodynamic drag of roof-mounted insulators for trains. J. Rail Rapid Transit 2019, 234, 834–846. [Google Scholar] [CrossRef]
- Bell, J.; Burton, D.; Thompson, M.; Herbst, A.; Sheridan, J. A wind-tunnel methodology for assessing the slipstream of high-speed trains. J. Wind. Eng. Ind. Aerodyn. 2017, 166, 1–19. [Google Scholar] [CrossRef]
- de Chant, L.J. The venerable 1/7th power law turbulent velocity profile: A classical nonlinear boundary value problem solution and its relationship to stochastic processes. Appl. Math. Comput. 2005, 161, 463–474. [Google Scholar] [CrossRef]
- Tschepe, J.; Nayeri, C.; Paschereit, C. On the influence of Reynolds number and ground conditions on the scaling of the aerodynamic drag of trains. J. Wind. Eng. Ind. Aerodyn. 2021, 213, 104594. [Google Scholar] [CrossRef]
- Barenblatt, G. Scaling laws for fully developed turbulent shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 1993, 248, 513–520. [Google Scholar] [CrossRef]
- Buschmann, M.H.; Gad-El-Hak, M. Debate Concerning the Mean-Velocity Profile of a Turbulent Boundary Layer. AIAA J. 2003, 41, 565–572. [Google Scholar] [CrossRef]
- George, W.K. Recent Advancements Toward the Understanding of Turbulent Boundary Layers. AIAA J. 2006, 44, 2435–2449. [Google Scholar] [CrossRef] [Green Version]
- Buschmann, M.H.; Gad-el-Hak, M. Turbulent boundary layers: Reality and myth. Int. J. Comput. Sci. Math. 2007, 1, 159–176. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Chorin, A.J.; Prostokishin, V.M. Analysis of Experimental Investigations of Self-Similar Intermediate Structures in Zero-Pressure Boundary Layers at Large Reynolds Numbers. arXiv 2000, arXiv:math-ph/0002004. [Google Scholar]
- Österlund, J. Experimental Studies of Zero Pressure-Gradient Turbulent Boundary-Layer Flow; KTH: Stockholm, Sweden, 1999; Available online: https://www.mech.kth.se/~jens/zpg/art/zpg_screen.pdf (accessed on 5 January 2022).
- Vallikivi, M.; Hultmark, M.; Smits, A. Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 2015, 779, 371–389. [Google Scholar] [CrossRef] [Green Version]
- Gorbushin, A.; Osipova, S.; Zametaev, V. Mean Parameters of an Incompressible Turbulent Boundary Layer on the Wind Tunnel Wall at Very High Reynolds Numbers. Flow Turbul. Combust 2021, 107, 31–50. [Google Scholar] [CrossRef]
- Marusic, I.; Chauhan, K.; Kulandaivelu, V.; Hutchins, N. Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 2015, 783, 379–411. [Google Scholar] [CrossRef] [Green Version]
- Oweis, G.; Winkel, E.; Cutbrith, J.; Ceccio, S.; Perlin, M.; Dowling, D. The mean velocity profile of a smooth-flat-plate turbulent boundary layer at high Reynolds number. J. Fluid Mech. 2010, 665, 357–381. [Google Scholar] [CrossRef]
- de Graaff, D.; Eaton, J. Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 2000, 422, 319–346. [Google Scholar] [CrossRef]
- Petrie, H.L.; Fontaine, A.A.; Sommer, S.T.; Brungart, T.A. Large Flat Plate Turbulent Boundary Layer Evaluation; Penn State Applied Research Laboratory Technical Memo File No. 89-207; Penn State Applied Research Laboratory: Reston, VA, USA, 1990; Available online: https://apps.dtic.mil/sti/pdfs/ADA225316.pdf (accessed on 5 January 2022).
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Hoerner, S. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Bakersfiled, CA, USA, 1965; Available online: http://ftp.demec.ufpr.br/disciplinas/TM240/Marchi/Bibliografia/Hoerner.pdf (accessed on 3 October 2021).
- Schultz-Grunow, F. New Fricitional Resistance Law for Smoothe Plates; NASA Tech Memo No. 986; NASA: Washington, DC, USA, 1941. Available online: https://ntrs.nasa.gov/citations/19930094430 (accessed on 5 January 2022).
- ITTC. Skin Friction and Turbulence Stimulation; Committee Report; ITTC: Ledegem, Belgium, 1957; Available online: https://ittc.info/media/3139/skin-friction-and-turbulence-stimulation.pdf (accessed on 5 January 2022).
- Rona, A.; Monti, M.; Airiau, C. On the generation of the mean velocity profile for turbulent boundary layers with pressure gradient under equilibrium conditions. Aeronaut. J. 2012, 116, 569–598. [Google Scholar] [CrossRef] [Green Version]
- Afzal, N.; Seena, A.; Bushra, A. Power Law Velocity Profile in Fully Developed Turbulent Pipe and Channel Flows. J. Hydraul. Eng. 2007, 133, 1080–1086. [Google Scholar] [CrossRef]










| Quantity | Formula |
|---|---|
| boundary layer thickness | |
| displacement thickness | |
| momentum thickness | |
| local friction coefficient | |
| friction drag coefficient | |
| velocity profile | |
| form parameter |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tschepe, J. On the Prediction of Boundary Layer Quantities at High Reynolds Numbers. Fluids 2022, 7, 114. https://doi.org/10.3390/fluids7030114
Tschepe J. On the Prediction of Boundary Layer Quantities at High Reynolds Numbers. Fluids. 2022; 7(3):114. https://doi.org/10.3390/fluids7030114
Chicago/Turabian StyleTschepe, Jonathan. 2022. "On the Prediction of Boundary Layer Quantities at High Reynolds Numbers" Fluids 7, no. 3: 114. https://doi.org/10.3390/fluids7030114