Broadband Terahertz Spectroscopy of Phonon-Polariton Dispersion in Ferroelectrics
Abstract
:1. Introduction
2. THz Dynamics of Ferroelectrics Studied by THz-TDS
2.1. THz-TDS
2.2. Bismuth Titanate
2.3. Barium Zirconate
3. Polariton Dispersion Studied by Far-IR Spectroscopy
3.1. Far-IR Spectroscopy
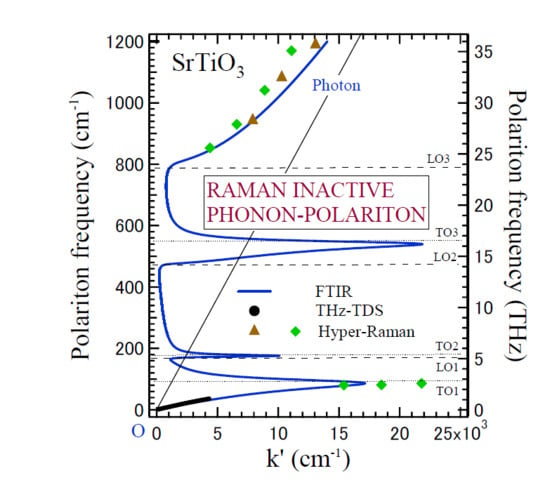
3.2. Strontium Titanate
3.3. Lithium Niobate
4. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Fano, F. Atomic Theory of electromagnetic interactions in dense materials. Phys. Rev. 1956, 103, 1202–1218. [Google Scholar] [CrossRef]
- Hopfield, J.J. Theory of the Contribution of Excitons to the Complex Dielectric Constant of Crystals. Phys. Rev. 1958, 112, 1555–1567. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
- Henry, C.H.; Hopfield, J.J. Raman scattering by polaritons. Phys. Rev. Lett. 1965, 15, 964–966. [Google Scholar] [CrossRef]
- Claus, R.; Merten, L.; Brandmüller, J. Light Scattering by Phonon-Polaritons; Springer: Berlin, Germany, 1975. [Google Scholar]
- Kawase, K.; Sato, M.; Taniuchi, T.; Ito, H. Coherent tunable THz-wave generation from LiNbO3 with monolithic grating coupler. Appl. Phys. Lett. 1996, 68, 2483–2485. [Google Scholar] [CrossRef]
- Barjker, A.S.; Loudon, R. Response Functions in the Theory of Raman Scattering by Vibrational and Polariton Modes in Dielectric Crystals. Rev. Mod. Phys. 1972, 44, 18–47. [Google Scholar] [CrossRef]
- Kojima, S.; Maczka, M. Broadband Phonon-Polariton Dispersion Relation of Ferroelectric LiTaO3 Crystals. Ferroelectrics 2018. Unpublished work. [Google Scholar]
- Fukumoto, T.; Okamoto, A.; Hattori, T.; Mitsuishi, A. Light scattering by polariton modes of KNbO3 in orthorhombic phase. Solid State Commun. 1975, 17, 427–431. [Google Scholar] [CrossRef]
- Kojima, S.; Nakamura, T. Observations of low-frequency phonon-polariton in barium sodium niobate. Jpn. J. Appl. Phys. 1980, 19, L609–L611. [Google Scholar] [CrossRef]
- Kojima, S. Low frequency phonon polaritons in several ferroelectrics. Ferroelectrics 1981, 37, 677–680. [Google Scholar] [CrossRef]
- Dougherty, T.P.; Wiederrecht, G.P.; Nelson, K.A. Impulsive stimulated Raman scattering experiments in the polariton regime. J. Opt. Soc. Am. B 1992, 9, 2179–2189. [Google Scholar] [CrossRef]
- Kojima, S.; Shibata, T.; Igawa, H.; Mori, T. Broadband terahertz time-domain spectroscopy: Crystalline and glassy drug materials. IOP Conf. Ser. Mater. Sci. Eng. 2014, 54, 012001. [Google Scholar] [CrossRef]
- Hoshina, T.; Kanehara, K.; Takeda, H.; Tsurumi, T. Terahertz dielectric response of single-domain BaTiO3 measured by far-infrared spectroscopic ellipsometry. Jpn. J. Appl. Phys. 2014, 53, 09PD03. [Google Scholar] [CrossRef]
- Van Exter, M.; Grischkowsky, D. Optical and electronic properties of doped silicon from 0.1 to 2 THz. Appl. Phys. Lett. 1998, 56, 1694–1696. [Google Scholar] [CrossRef]
- Wada, M.; Doi, Y.; Inoue, K.; Haus, J.W.; Yuan, Z. A simple-cubic photonic lattice in silicon. Appl. Phys. Lett. 1997, 70, 2966–2968. [Google Scholar] [CrossRef]
- Kojima, S.; Tsumura, N.; Takeda, M.W.; Nishizawa, S. Far-infrared phonon-polariton dispersion probed by terahertz time-domain spectroscopy. Phys. Rev. B 2003, 67, 035102. [Google Scholar] [CrossRef]
- Kojima, S.; Shimada, S. Soft mode spectroscopy of bismuth titanate single crystals. Physica B 1996, 219–220, 617–619. [Google Scholar] [CrossRef]
- Kurosawa, T. Polarization Waves in Solids. J. Phys. Soc. Jpn. 1961, 16, 1298–1308. [Google Scholar] [CrossRef]
- Dobal, P.S.; Dixit, A.; Katiyar, R.S.; Yu, Z.; Guo, R.; Bhalla, A.S. Micro-Raman scattering and dielectric investigations of phase transition behavior in the BaTiO3–BaZrO3 system. J. Appl. Phys. 2001, 89, 8085–8091. [Google Scholar] [CrossRef]
- Akbarzadeh, A.R.; Kornev, I.; Malibert, C.; Bellaiche, L.; Kiat, J.M. Combined theoretical and experimental study of the low-temperature properties of BaZrO3. Phys. Rev. B 2005, 72, 205104. [Google Scholar] [CrossRef]
- Helal, M.A.; Mori, T.; Kojima, S. Softening of infrared-active mode of perovskite BaZrO3 proved by terahertz time-domain spectroscopy. Appl. Phys. Lett. 2015, 106, 182904. [Google Scholar] [CrossRef] [Green Version]
- Helal, M.A.; Mori, T.; Kojima, S. Terahertz time-domain spectroscopy and Raman scattering studies of incipient ferroelectric BaZrO3. Ferroelectrics 2016, 499, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Nuzhnyy, D.; Petzelt, J.; Savinov, M.; Ostapchuk, T.; Bovtun, V.; Kempa, M.; Hlinka, J.; Buscaglia, V.; Buscaglia, M.T.; Nanni, P. Broadband dielectric response of Ba(Zr,Ti)O3 ceramics: From incipient via relaxor and diffuse up to classical ferroelectric behavior. Phys. Rev. B 2012, 86, 014106. [Google Scholar] [CrossRef]
- Evarestov, R.A. Hybrid density functional theory LCAO calculations on phonons in Ba(Ti,Zr,Hf)O3. Phys. Rev. B 2011, 83, 014105. [Google Scholar] [CrossRef]
- Luspin, Y.; Servoin, J.L.; Gervais, F. Soft mode spectroscopy in barium titanate. J. Phys. C 1980, 13, 3761–3773. [Google Scholar] [CrossRef]
- Presting, H.; Sanjurjo, J.A.; Vogt, H. Mode softening in cubic BaTiO3 and the problem of its adequate description. Phys. Rev. 1983, 28, 6097–6099. [Google Scholar] [CrossRef]
- Muller, K.A.; Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 1979, 19, 3593–3602. [Google Scholar] [CrossRef]
- Spitzer, W.G.; Miller, R.C.; Kleinman, D.A.; Howarth, L.E. Far Infrared Dielectric Dispersion in BaTiO3, SrTiO3, and TiO2. Phys. Rev. 1962, 126, 1710–1721. [Google Scholar] [CrossRef]
- Kanehara, K.; Hoshina, T.; Takeda, H.; Tsurumi, T. Measurement of ionic polarization of SrTiO3 single crystal by far-infrared spectroscopic ellipsometry. Appl. Phys. Lett. 2014, 105, 042901. [Google Scholar] [CrossRef]
- Matsumoto, N.; Fujii, T.; Kageyama, K.; Takagi, H.; Nagashima, T.; Hangyo, M. Measurement of the Soft-Mode Dispersion in SrTiO3 by Terahertz Time-Domain Spectroscopic Ellipsometry. Jpn. J. Appl. Phys. 2002, 48, 19KC11. [Google Scholar]
- Kojima, S.; Mori, T. Terahertz time-domain spectroscopy of Raman inactive phonon-polariton in strontium titanate. Ferroelectrics 2016, 499, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Kojima, S.; Maczka, M. Raman inactive phonon-polariton dispersion in quantum paraelectric SrTiO3 crystals studied by FTIR. Ferroelectrics 2018, 524, 1–8. [Google Scholar] [CrossRef]
- Denisov, V.N.; Mavrin, B.N.; Podobedev, V.B.; Sterin, K.E. Hyper Raman scattering by polaritons in centrally symmetric SrTiO3 crystal. JETP Lett. 1980, 31, 102–105. [Google Scholar]
- Inoue, K.; Asai, N.; Samejima, T. Observation of the phonon polariton in the centrosymmetric crystal of SrTiO3 by Hyper Raman scattering. J. Phys. Soc. Jpn. 1980, 48, 1787–1788. [Google Scholar] [CrossRef]
- Matthias, B.T.; Remeika, J.P. Ferroelectricity in the ilmenite structure. Phys. Rev. 1949, 76, 1886–1887. [Google Scholar] [CrossRef]
- Bazzan, M.; Fontana, M. Preface to Special Topic: Lithium Niobate Properties and Applications: Reviews of Emerging Trends. Appl. Phys. Rev. 2015, 2, 040501. [Google Scholar] [CrossRef] [Green Version]
- Lee, A.J.; Pask, H.M. Cascaded stimulated polariton scattering in a Mg:LiNbO3 terahertz laser. Optics Express. 2015, 23, 8687. [Google Scholar] [CrossRef] [PubMed]
- Niizeki, N.; Yamada, T.; Toyoda, H. Growth Ridges, Etched Hillocks, and Crystal Structure of Lithium Niobate. Jpn. J. Appl. Phys. 1967, 6, 318–327. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Levinstein, H.J.; Reddy, J.M. Ferroelectric lithium niobate. 4. Single crystal neutron diffraction study at 24 °C. J. Phys. Chem. Solids 1966, 27, 1013–1018. [Google Scholar] [CrossRef]
- Axe, J.D.; O’Kane, D.F. Infrared dielectric dispersin of LiNbO3. Appl. Phys. Lett. 1966, 9, 58–60. [Google Scholar] [CrossRef]
- Schaufele, R.F.; Weber, M.J. Raman Scattering by Lithium Niobate. Phys. Rev. 1966, 152, 705–708. [Google Scholar] [CrossRef]
- Barker, A.S., Jr. Loudon, R. Dielectric Properties and Optical Phonons in LiNbO3. Phys. Rev. 1967, 158, 433–445. [Google Scholar] [CrossRef]
- Kaminow, I.P.; Johnston, W.D., Jr. Quantitative Determination of Sources of the Electro-Optic Effect in LiNbO3 and LiTaO3. Phys. Rev. 1967, 160, 519–522. [Google Scholar] [CrossRef]
- Claus, R.; Borstel, G.; Wiesendanger, E.; Steffan, L. Assignments of Optical Phonon Modes in LiNbO3. Phys. Rev. B 1972, 6, 4878–4879. [Google Scholar] [CrossRef]
- Kojima, S. Composition variation of optical phonon damping of lithium niobate crystals. Jpn. J. Appl. Phys. 1993, 32, 4373–4376. [Google Scholar] [CrossRef]
- Margueron, S.; Bartasyte, A.; Glazer, A.M.; Simon, E.; Hlinka, J.; Gregora, I.; Gleize, J. Resolved E-symmetry zone-center phonons in LiTaO3 and LiNbO3. J. Appl. Phys. 2012, 111, 104105. [Google Scholar] [CrossRef]
- Caciuc, V.; Postnikov, A.V.; Borstel, B. Ab initio structure and zone-center phonons in LiNbO3. Phys. Rev. B 2000, 61, 8806–8813. [Google Scholar] [CrossRef]
- Veithen, M.; Ghosez, P. First-principles study of the dielectric and dynamical properties of lithium niobate. Phys. Rev. B 2002, 65, 214302. [Google Scholar] [CrossRef]
- Hermet, P.; Veithen, M.; Ghosez, P. First-principles calculations of the nonlinear optical susceptibilities and Raman scattering spectra of lithium niobate. J. Phys. Condens. Matter 2007, 19, 456202. [Google Scholar] [CrossRef]
- Sanna, S.; Neufeld, S.; Rusing, M.; Berth, G.; Zrenner, A.; Schmidt, W.G. Raman scattering efficiency in LiTaO3 and LiNbO3 crystals. Phys. Rev. B 2015, 91, 224302. [Google Scholar] [CrossRef]
- Kojima, S.; Kanehara, K.; Hoshina, T.; Tsurumi, T. Optical phonons and polariton dispersions of congruent LiNbO3 studied by far-infrared spectroscopic ellipsometry and Raman scattering. Jpn. J. Appl. Phys. 2016, 55, 10TC02. [Google Scholar] [CrossRef]
- Kojima, S.; Kitahara, H.; Wada Takeda, M.; Nishizawa, S. Terahertz time domain spectroscopy of phonon-polaritons in ferroelectric lithium niobate crystals. Jpn. J. Appl. Phys. 2002, 41, 7033–7037. [Google Scholar] [CrossRef]







© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kojima, S. Broadband Terahertz Spectroscopy of Phonon-Polariton Dispersion in Ferroelectrics. Photonics 2018, 5, 55. https://doi.org/10.3390/photonics5040055
Kojima S. Broadband Terahertz Spectroscopy of Phonon-Polariton Dispersion in Ferroelectrics. Photonics. 2018; 5(4):55. https://doi.org/10.3390/photonics5040055
Chicago/Turabian StyleKojima, Seiji. 2018. "Broadband Terahertz Spectroscopy of Phonon-Polariton Dispersion in Ferroelectrics" Photonics 5, no. 4: 55. https://doi.org/10.3390/photonics5040055