1. Introduction
Reduced order models (ROM) aims at reducing the computational complexity and, in turn, the simulation time of large-scale dynamical systems by approximating the state-space to much lower dimensions. This yields reduced models that can produce nearly the same input/output response characteristics as the original ones. Approaches to construct ROMs by projection include the Proper Orthogonal Decomposition (POD) method [
1], the balanced truncation (BT) [
2], the Krylov subspace projection methods, the trajectory-piecewise linear (TPWL) techniques [
3] and variants of them. Among these approaches, the POD method is perhaps the most popular one. For example, the POD was successfully applied to a number of areas [
4,
5,
6,
7,
8,
9,
10,
11].
For POD projection type model reduction, the process typically consists of an offline stage followed by an online stage. In the offline stage, the low dimension solution space, also called as the POD subspace, is generated and a reduced system for the problem at hand is constructed by projecting onto the low dimension solution space; in the online stage, on the other hand, an approximated solution is obtained by integrating the reduced dynamical system. The online solution relies only on the pre-computed quantities from the offline stage. Therefore, a good approximation from the reduced model can be expected only if the offline information is a good representation of the problem with initial input parameters.
Much progress on adaptivity has been made in the context of model reduction. Offline adaptive methods [
12] seek to provide a better reduce solution space while the reduced system is constructed in the offline stage. However, once the reduced system is derived, it stays fixed and is kept unchanged in the online stage. Therefore, the online solution relies only on the pre-computed information from the offline stage which is not incorporated at the online phase. Unlike the offline adaptation, online adaptive methods modify the reduced system during the computations in the integration stage. Most of the existing global online adaptive methods [
13,
14,
15] rely only on precomputed quantities from the offline stage. We consider here a different approach whereby online adaptivity is performed by incorporating new data that becomes available in the online stage.
We use the POD Galerkin method for global model reduction. However, for a nonlinear system, projection alone is not sufficient to deliver a computationally efficient model, since the nonlinear terms require computations that often render solving the reduced system almost as expensive as solving the full order system. To deal with nonlinearities, we apply the Discrete Empirical Interpolation Method (DEIM) proposed in [
16]. The DEIM samples the nonlinear terms at selected interpolation points and then combines interpolation and projection to obtain an approximation in a low-dimensional DEIM space.
In the linear system setting, one can compute the projection matrices based on the fixed operators offline, that is, outside of the time dependent loop, and perform the reduction by projecting directly onto a much smaller subspace as in Equation (2). However, for nonlinear systems, as in the case of flow in heterogeneous porous media, one cannot perform such projection without having to recompute the operators for every time step. In this case, the best choice is to compute the projection matrices offline and perform the projection and integration of the reduced model online. This setting is particularly useful for the POD-DEIM-based model reduction, whereby the projection matrices are computed offline and are based solely on runs of the fine scale model. In summary, in the offline stage, we construct the reduced order model; in the online stage, given particular parameters or inputs, the reduced model can be approximated efficiently and integrated in time. Online computations have costs that may not depend on the size of the fine scale model. For this reason, we perform the online adaptivity infrequently.
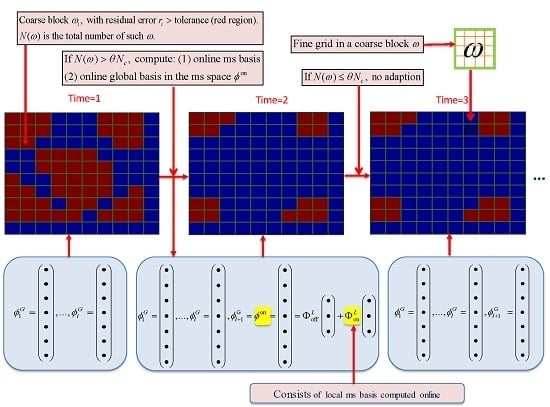
In the online stage, we propose a criterion to decide when updates are required. Once the criterion is satisfied, we adapt the POD subspaces, the DEIM space and the DEIM interpolation points for the nonlinear functions by incorporating new data that becomes available online. For the adaption of the POD subspace, we propose a local-global strategy. First, instead of global error indicators based on the residual which are expensive to compute, we use local error indicators to monitor when global POD basis adaption is needed. By using local error indicators, the computational time can be reduced as one avoids computing global error indicators. Secondly, we employ a local model order reduction method,
i.e., the generalized multiscale finite element method (GMsFEM) [
17,
18,
19,
20], to solve the global residual problem to get the new POD basis function. Based on local error indicators (see [
21,
22,
23,
24] for local error indicators for GMsFEM), some local multiscale basis functions are updated and used to compute the online global modes inexpensively. For the adaption of DEIM, we employ a modified low rank updates method investigated in [
25], which introduces computational costs that scale linearly in the number of unknowns of the full-order system. We remark that the offline local-global approaches have been studied in the literature [
26,
27,
28,
29]. In the proposed method, we develop online multiscale basis functions for both local and global updates.
Our particular interest here is subsurface flow problems. POD techniques were first used by Vermeulen
et al. [
30] in the context of subsurface flow problems, e.g., that was a groundwater flow problem with a single water component. Jansen
et al. [
9,
31] applied POD to a two-phase oil-water flow. In [
32] TPWL was introduced to solve an oil-water flow system. A local-global multi-scale model reduction was proposed in [
33]. A constraint reduction based on POD-TPWL was present in [
34]. In [
11,
35], POD-DEIM model reduction was used to solve a two-phase flow problem with gravity. However, these methods can only deal with cases that the variation in inputs is within a certain range,
i.e., the offline procedure should be able to anticipate almost all the the dynamics of the online system. In many applications, such as optimization and history matching, the final solution trajectory may be hard to predict before the problem is solved. Therefore, a good POD subspace just from using the offline information may not yield robust approximation solutions. Here, we propose to adapt the reduced system by using online data in the online stage. Our numerical results show that one can achieve a good approximation of the solution at a reduced cost.
This paper is organized as follows. In
Section 2, the concept of model reduction based on POD-DEIM is given; a short review of POD and DEIM is presented. In
Section 3, online adaptive POD is described in
Section 3.1, and a discussion of online adaptive DEIM approximation is described in
Section 3.2. Applications to single-phase flow and two-phase flow problems are given in
Section 4.1 and
Section 4.2 respectively. The paper ends with our conclusion in
Section 5.
2. Preliminaries
In this section, we will first review the concept of POD-DEIM based model reduction method, which can reduce the dimension of large-scale ODE systems regardless of their origin. A large source of such systems is the semidiscretization of time dependent PDEs. After spatial discretization for a nonlinear PDE, we get a system of nonlinear ODEs of the form
where
is a constant matrix, and
is a nonlinear function.
We start our exposition by briefly reviewing the global model reduction framework. Let
be an orthonormal matrix consisting of reduced basis. Replacing
in Equation (1) by
, and by Galerkin projection of the system (1) onto
, we get the reduced system of (1) (the super index
T means the transpose of a matrix):
The quality of the above POD Galerkin approximation depends on the choice of reduced basis. Snapshot based POD constructs a set of global basis functions from a singular value decomposition (SVD) of snapshots, which are discrete samples of trajectories associated with a particular set of boundary conditions and inputs. It is expected that the samples will be representative of the solution manifold of the problem of interest. Among the various techniques for obtaining a reduced basis, POD constructs a reduced basis that is optimal in the sense that a certain approximation error concerning the snapshots is minimized. The details of POD are presented in
Section 2.1.
To evaluate the nonlinear term
in Equation (2), we first need to project the solution from the reduced space to the fine solution space, then evaluate the nonlinear function
at all the
n fine components, finally we project the
n fine components back onto
. The process results in a cost that is as expensive as solving the original system. To handle this inefficiency, we use DEIM [
16], which is reviewed in
Section 2.2.
The POD-DEIM model reduction method consists of two stages. In the offline stage, given some inputs, which can be boundary conditions, or control parameters, we run several simulations for the system described by Equation (1) to produce snapshots for the solution states (pressure, saturation or concentration in subsurface flow simulation context) and nonlinear functions. POD is performed to construct the reduced subspaces for the states, and interpolants for the nonlinear functions. In the online stage, the approximate solution of the problem is obtained by writing the solution as a linear combination of the reduced basis, which was fixed at the offline phase. Next, we describe in more details the aforementioned process.
2.1. Proper Orthogonal Decomposition
The POD basis in Euclidean space is specified formally in this section. We refer to [
36] for more details on the POD basis in general Hilbert space.
Given a set of snapshots
, let
and
. A POD basis of dimension
is a set of orthonormal vectors
whose linear span best approximates the space
. The basis set
solves the minimization problem
with
.
It is well known that the solution to Equation (3) is provided by the set of the left singular vectors of the
snapshot matrix . Applying SVD to
, we get
where
,
are the left and right projection matrices respectively, and
with
. The rank of
is
. The first
k column vectors
of
are selected as the POD basis (the criterion to decide
k is explained later ). The minimum
-norm error from approximating the snapshots using the POD basis is then given by
The appropriate number of POD basis to be retained for a prescribed accuracy can be determined, for example, by means of the fractional energy (see discussions in [
37] for selecting modes):
A small number of POD basis is retained if the singular values decay fast. This decay depends on the intrinsic dynamics of the system and the selection of the snapshots. In the next section, we review DEIM, which is applied to reduce the nonlinear terms.
2.2. Discrete Empirical Interpolation Method (DEIM)
In the offline stage, we get the snapshots of the nonlinear function
as:
By applying POD to the above snapshot matrix and selecting the first
m eigen-vectors corresponding to the dominant eigen-values, we obtain the DEIM basis
. DEIM [
16] selects
m distinct interpolation points
and assemble the DEIM interpolation points matrix
where
is the
i-th canonical unit vector. The DEIM interpolant of
is defined by
. The DEIM approximation of
is derived, based on
, as
where
samples
at
m components only. In what follows, local model reduction will be reviewed.
2.3. Local Model Order Reduction via GMsFEM
We will give a brief overview of the local model reduction using the GMsFEM [
17,
18,
19,
20]. Let
be a usual conforming partition of the domain Ω into finite elements called coarse elements, and
H is the coarse mesh size. Then, each coarse element is divided into a connected union of fine elements, which are conforming across coarse element faces. This fine grid partition is denoted by
with
h as fine mesh size . The fine grid is used to construct the locally supported multiscale basis functions, and compute the reference (fine) solution in the numerical examples. The reference solution is computed on the fine grid. Let
be the set of nodes on the coarse grid with
being the number of nodes in
. For each coarse node
, a coarse neighborhood is defined as
. An illustration of the definitions is given in
Figure 1. The multiscale basis functions are nodal based and supported on coarse neighborhoods. Specifically, for each coarse node
we construct a set of basis functions
such that each
is supported on the coarse neighborhood
. Note that
can be different for different nodes.
Let
ω be a given coarse neighborhood, to construct the multiscale basis functions supported on
ω, first we construct a snapshot space
.
is a set of functions defined on
ω and contains all or most necessary information of the fine scale solution restricted to
. A typical choice of
is local flow solutions, which are constructed by solving local problems with all possible boundary conditions. This can be expensive and for this reason, one can use randomized boundary conditions (see [
38,
39]) and construct only a few more snapshots than the number of desired local basis functions. Next, we construct the offline space
for
ω by performing a spectral decomposition of
, and choosing the eigenvectors corresponding to the largest eigenvalues. The offline space is defined as
. We refer to [
17,
40] for details. The above computations are performed in the offline stage. For time dependent problems, as time advancing,
may not be good enough to represent the behavior of the full resolved solution at some time instants. We use an adaptive enrichment algorithm which allows one to use more basis functions in regions with large errors. We refer to [
40] for details.