Molecular Processes Leading to Shear Banding in Entangled Polymeric Solutions
Abstract
:1. Introduction
2. DPD Model Development and Validation
3. Results and Discussion
3.1. Quiescent Properties
3.2. Steady-State Shear Flow: Rheology and Network Topology
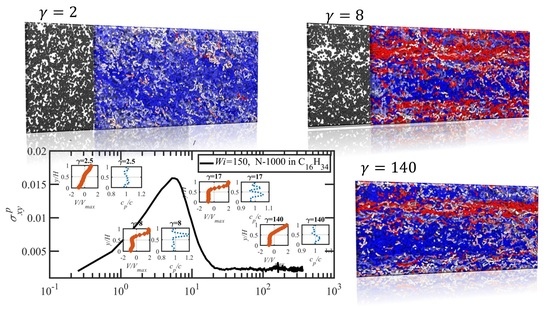
3.3. Startup of Shear Flow: Transient Shear Banding, Reverse Flow, and Concentration Fluctuations
4. Conclusions
- Both N-1000 PE hexadecane and benzene solutions exhibited a monotonic steady-state shear stress profile when plotted versus applied strain rate with a very broad stress plateau at intermediate .
- Under startup of shear flow, both solutions initially exhibited uniform, linear uniform velocity profiles and homogeneous polymer concentration. However, at an applied strain approximately that at which a maximum occurred in the overshoot of the first normal stress difference, transient shear bands developed within the simulation cell for a period of time ranging up to several hundred strain units. During this strain period, the velocity profile across the cell in the gradient direction was not uniform, with two or more local zones of relatively low and high strain rates. At high strains, the shear bands dissipated and the system attained steady-state behavior, with a uniform, linear velocity profile across the simulation cell and a homogeneous concentration. This transient shear banding was observed throughout the applied corresponding to the shear stress plateau.
- Regardless of whether or not shear bands occurred, the shear stress was homogeneous throughout the simulation cell, as verified using various sublayers of the simulation cell in the gradient direction. However, during the lifetime of the shear bands, the first normal stress difference was significantly different between the slow and fast bands, with a higher value in the fast bands where the individual molecules were more highly extended.
- When the effective of the slow band is less than , the polymer concentration is inhomogeneous with an accumulation of chain particles in the slow band and a depletion in the fast band. However, when the effective of the slow band is larger than , the opposite trend is observed, with chain particles preferentially migrating into the fast band and depleting the slow band. These results concerning nonuniform concentration profiles in shear flow of polymer solutions are consistent with those of prior experimental work [35,36], although evidence presented herein implies that shear bands develop solely due to the polymer chain dynamics, rather than necessarily being prerequisite to a nonuniform concentration profile, as suggested by Burroughs et al. The nonuniform concentration profiles generated in the present simulation work appear to be merely the result of different chain dynamics arising in the fast and slow bands.
- Variations in local orientation and stretching of the tube network segments and the commensurate destruction of the entanglement network appear to be the primary driving mechanisms of the transient shear banding. Molecules within the fast and slow bands experience different topological environments, as induced by the stochastic nature of the flow. Molecules within the fast bands have higher fractional extension and experience quasiperiodic extension/retraction cycles, whereas those in the slow band have lower fractional extension and tend to exhibit a flow-aligning behavior during the lifetime of the shear bands.
- In some instances, a mild reverse flow (i.e., a negative local velocity) was observed after the onset of shear banding. This phenomenon resulted from elastic recoil associated with the molecules within the slow band upon inception of shear banding as the entanglement network fractured along the interface between the bands. The entanglement kink number within the slow band remained significantly higher than the concomitant number in the fast band. Reverse flow was only observed in the hexadecane solution and not the benzene solution. This might be indicative of the much lower number of entanglement kinks in the benzene solution at low applied .
- It is highly likely that a multitude of possible shear bands could be observed if further simulations had been possible, due to the stochastic nature of the DPD algorithm (and experiments). At the stress plateau, the stress values, although strictly monotonic, are increasing at such a low slope that the system dynamics could temporarily become trapped in any number of comparable stress states at any particular time, resulting in a chaotic instability that gradually evolves into a steady-state uniform velocity profile at high strain values. This type of instability could conceivably generate a spectrum of shear bands of differing strain rate within which is evolving in time.
- The underlying mechanism of shear band formation in polymer melts and solutions is essentially the same, being driven by flow-induced disentanglement and localized, individual chain dynamics that are stochastic by nature. In dense melts, however, the concentration inhomogeneity associated with shear banding observed in solutions is effectively negligible. Shear bands develop at shear stress values that possess a multiplicity of compatible shear rates. Different shear-rate zones correspond to varying configurational dynamics of the constituent polymer molecules. Because of the broad spectrum of available molecular configurations of the chains under flow, it is possible that multiple configurationally dynamic states can be associated with a single value of imposed shear stress. Hence, the primary physical mechanism underlying shear banding in both polymer solutions and melts is evidently the same.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalika, D.S.; Denn, M.M. Wall slip and extrudate distortion in Linear low-density polyethylene. J. Rheol. 1987, 31, 815–834. [Google Scholar] [CrossRef]
- Denn, M.M. Extrusion instabilities and wall slip. Ann. Rev. Fluid Mech. 2001, 33, 265–287. [Google Scholar] [CrossRef] [Green Version]
- de Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S. Dynamics of concentrated polymer systems. Part 2.—Molecular motion under flow. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- Adams, J.M.; Fielding, S.M.; Olmsted, P.D. Transient shear banding in entangled polymers: A study using the Rolie-Poly model. J. Rheol. 2011, 55, 1007–1032. [Google Scholar] [CrossRef] [Green Version]
- Fielding, S.; Olmsted, P. Nonlinear dynamics of an interface between shear bands. Phys. Rev. Lett. 2006, 96, 104502. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.M.; Olmsted, P.D. Nonmonotonic models are not necessary to obtain shear banding phenomena in entangled polymer solutions. Phys. Rev. Lett. 2009, 102, 067801. [Google Scholar] [CrossRef]
- Moorcroft, R.L.; Fielding, S.M. Criteria for shear banding in time-dependent flows of complex fluids. Phys. Rev. Lett. 2013, 110, 086001. [Google Scholar] [CrossRef] [Green Version]
- Moorcroft, R.L.; Fielding, S.M. Shear banding in time-dependent flows of polymers and wormlike micelles. J. Rheol. 2014, 58, 103–147. [Google Scholar] [CrossRef] [Green Version]
- Moorcroft, R.L.; Cates, M.E.; Fielding, S.M. Age-dependent transient shear banding in soft glasses. Phys. Rev. Lett. 2011, 106, 055502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boudaghi, M.; Edwards, B.J.; Khomami, B. Microstructural evolution and reverse flow in shear-banding of entangled polymer melts. Soft Matter 2023, 19, 410–429. [Google Scholar] [CrossRef]
- Boudaghi-Khajehnobar, M.; Edwards, B.J.; Khomami, B. Effects of chain length and polydispersity on shear banding in simple shear flow of polymeric melts. Soft Matter 2020, 16, 6468–6483. [Google Scholar] [CrossRef]
- Mohagheghi, M.; Khomami, B. Molecularly based criteria for shear banding in transient flow of entangled polymeric fluids. Phys. Rev. E 2016, 93, 062606. [Google Scholar] [CrossRef] [Green Version]
- Mohagheghi, M.; Khomami, B. Elucidating the flow-microstructure coupling in entangled polymer melts. Part II: Molecular mechanism of shear banding. J. Rheol. 2016, 60, 861–872. [Google Scholar] [CrossRef]
- Mohagheghi, M.; Khomami, B. Molecular processes leading to shear banding in well entangled polymeric melts. ACS Macro Lett. 2015, 4, 684–688. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Q.; Ravindranath, S.; Boukany, P. Homogeneous shear, wall slip, and shear banding of entangled polymeric liquids in simple-shear rheometry: A roadmap of nonlinear rheology. Macromolecules 2011, 44, 183–190. [Google Scholar] [CrossRef]
- Helfand, E.; Fredrickson, G.H. Large fluctuations in polymer solutions under shear. Phys. Rev. Lett. 1989, 62, 2468–2471. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.; Helfand, E. Concentration fluctuations in sheared polymer solutions. Macromolecules 1995, 28, 3869–3880. [Google Scholar] [CrossRef]
- Onuki, A. Shear-induced phase separation in polymer solutions. J. Phys. Soc. Jpn. 1990, 59, 3427–3430. [Google Scholar] [CrossRef]
- Onuki, A.; Kawasaki, K. Dynamics and Patterns in Complex Fluids: New Aspects of the Physics-Chemistry Interface; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 52. [Google Scholar]
- Milner, S.T. Dynamical theory of concentration fluctuations in polymer solutions under shear. Phys. Rev. E 1993, 48, 3674–3691. [Google Scholar] [CrossRef]
- Wu, X.L.; Pine, D.J.; Dixon, P.K. Enhanced concentration fluctuations in polymer solutions under shear flow. Phys. Rev. Lett. 1991, 66, 2408–2411. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, T.; Fujioka, K. Shear-enhanced concentration fluctuations in polymer solutions as observed by flow light scattering. J. Phys. Soc. Jpn. 1991, 60, 356–359. [Google Scholar] [CrossRef]
- Morfin, I.; Lindner, P.; Boue, F. Temperature and shear rate dependence of small angle neutron scattering from semidilute polymer solutions. Macromolecules 1999, 32, 7208–7223. [Google Scholar] [CrossRef]
- Saito, S.; Hashimoto, T.; Morfin, I.; Lindner, P.; Boué, F. Structures in a semidilute polymer solution induced under steady shear flow as studied by small-angle light and neutron scattering. Macromolecules 2002, 35, 445–459. [Google Scholar] [CrossRef]
- van Egmond, J.W. Effect of stress- structure coupling on the rheology of complex fluids: Poor polymer solutions. Macromolecules 1997, 30, 8045–8057. [Google Scholar] [CrossRef]
- Milner, S.T. Hydrodynamics of semidilute polymer solutions. Phys. Rev. Lett. 1991, 66, 1477–1480. [Google Scholar] [CrossRef]
- Peterson, J.D.; Fredrickson, G.H.; Gary Leal, L. Shear induced demixing in bidisperse and polydisperse polymer blends: Predictions from a multifluid model. J. Rheol. 2020, 64, 1391–1408. [Google Scholar] [CrossRef]
- Stieger, M.; Richtering, W. Shear-induced phase separation in aqueous polymer solutions: Temperature-sensitive microgels and linear polymer chains. Macromolecules 2003, 36, 8811–8818. [Google Scholar] [CrossRef]
- Fielding, S.M.; Olmsted, P.D. Flow phase diagrams for concentration-coupled shear banding. Europ. Phys. J. E 2003, 11, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Olmsted, P.D.; Radulescu, O.; Lu, C.Y. Johnson–Segalman model with a diffusion term in cylindrical Couette flow. J. Rheol. 2000, 44, 257–275. [Google Scholar] [CrossRef] [Green Version]
- Johnson Jr, M.W.; Segalman, D. A model for viscoelastic fluid behavior which allows non-affine deformation. J. Non-Newton. Fluid Mech. 1977, 2, 255–270. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Graham, R.S. Simple constitutive equation for linear polymer melts derived from molecular theory: Rolie–Poly equation. J. Non-Newton. Fluid Mech. 2003, 114, 1–12. [Google Scholar] [CrossRef]
- Cromer, M.; Villet, M.C.; Fredrickson, G.H.; Leal, L.G. Shear banding in polymer solutions. Phys. Fluids 2013, 25, 051703. [Google Scholar] [CrossRef]
- Burroughs, M.C.; Zhang, Y.; Shetty, A.M.; Bates, C.M.; Leal, L.G.; Helgeson, M.E. Flow-induced concentration nonuniformity and shear banding in entangled polymer solutions. Phys. Rev. Lett. 2021, 126, 207801. [Google Scholar] [CrossRef]
- Burroughs, M.C.; Zhang, Y.; Shetty, A.; Bates, C.M.; Helgeson, M.E.; Leal, L.G. Flow-concentration coupling determines features of nonhomogeneous flow and shear banding in entangled polymer solutions. J. Rheol. 2023, 67, 219–239. [Google Scholar] [CrossRef]
- Shin, S.; Dorfman, K.D.; Cheng, X. Shear-banding and superdiffusivity in entangled polymer solutions. Phys. Rev. E 2017, 96, 062503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic simulations of hard-sphere suspensions under steady shear. Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Nafar, M.H.; Boudaghi-Khajehnobar, M.; Edwards, B.J.; Khomami, B. High-fidelity scaling relationships for determining dissipative particle dynamics parameters from atomistic molecular dynamics simulations of polymeric liquids. Sci. Rep. 2020, 10, 1–13. [Google Scholar]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Flow-induced phase separation and crystallization in entangled polyethylene solutions under elongational flow. Macromolecules 2020, 53, 6432–6451. [Google Scholar] [CrossRef]
- Nikunen, P.; Vattulainen, I.; Karttunen, M. Reptational dynamics in dissipative particle dynamics simulations of polymer melts. Phys. Rev. E 2007, 75, 036713. [Google Scholar] [CrossRef] [Green Version]
- Mohagheghi, M.; Khomami, B. Elucidating the flow-microstructure coupling in the entangled polymer melts. Part I: Single chain dynamics in shear flow. J. Rheol. 2016, 60, 849–859. [Google Scholar] [CrossRef]
- Boudaghi, M.; Nafar Seddashti, M.H.; Edwards, B.J.; Khomami, B. Elucidating the role of network topology dynamics on the coil-stretch transition hysteresis in extensional flow of entangled polymer melts. J. Rheol. 2022, 66, 551–569. [Google Scholar] [CrossRef]
- Durchschlag, H.; Zipper, P. Calculation of the partial volume of organic compounds and polymers. In Ultracentrifugation; Springer: Berlin/Heidelberg, Germany, 1994; pp. 20–39. [Google Scholar]
- Chelli, R.; Cardini, G.; Procacci, P.; Righini, R.; Califano, S.; Albrecht, A. Simulated structure, dynamics, and vibrational spectra of liquid benzene. J. Chem. Phys. 2000, 113, 6851–6863. [Google Scholar] [CrossRef]
- Chelli, R.; Cardini, G.; Ricci, M.; Bartolini, P.; Righini, R.; Califano, S. The fast dynamics of benzene in the liquid phase. Part II. A molecular dynamics simulation. Phys. Chem. Chem. Phys. 2001, 3, 2803–2810. [Google Scholar] [CrossRef]
- Maiti, A.; McGrother, S. Bead–bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594–1601. [Google Scholar] [CrossRef] [PubMed]
- Barton, A.F. Handbook of Poylmer-Liquid Interaction Parameters and Solubility Parameters; CRC Press: Boca Raton, FL, USA, 1990; Volume 73. [Google Scholar]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Microphase separation in entangled polymeric solutions in extensional flows. Bull. Am. Phys. Soc. 2020, 65. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.M.; Edwards, B.J.; Keffer, D.J.; Khomami, B. Dynamics of individual molecules of linear polyethylene liquids under shear: Atomistic simulation and comparison with a free-draining bead-rod chain. J. Rheol. 2010, 54, 283–310. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Individual molecular dynamics of an entangled polyethylene melt undergoing steady shear flow: Steady-state and transient dynamics. Polymers 2019, 11, 476. [Google Scholar] [CrossRef] [Green Version]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Individual chain dynamics of a polyethylene melt undergoing steady shear flow. J. Rheol. 2015, 59, 119–153. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Steady shearing flow of a moderately entangled polyethylene liquid. J. Rheol. 2016, 60, 1227–1244. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Kim, J.M.; Edwards, B.J.; Keffer, D.J.; Khomami, B. Single-chain dynamics of linear polyethylene liquids under shear flow. Phys. Lett. A 2009, 373, 769–772. [Google Scholar] [CrossRef]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two-and three-dimensional polymeric systems. Comp. Phys. Comm. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Kröger, M. Combined molecular algorithms for the generation, equilibration and topological analysis of entangled polymers: Methodology and performance. Inter. J. Mol. Sci. 2009, 10, 5054–5089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kröger, M.; Dietz, J.D.; Hoy, R.S.; Luap, C. The Z1+ package: Shortest multiple disconnected path for the analysis of entanglements in macromolecular systems. Comp. Phys. Comm. 2023, 283, 108567. [Google Scholar] [CrossRef]
- Padding, J.T.; Briels, W.J. Uncrossability constraints in mesoscopic polymer melt simulations: Non-Rouse behavior of C120H242. J. Chem. Phys. 2001, 115, 2846–2859. [Google Scholar] [CrossRef] [Green Version]
- Everaers, R. Topological versus rheological entanglement length in primitive-path analysis protocols, tube models, and slip-link models. Phys. Rev. E 2012, 86, 022801. [Google Scholar] [CrossRef] [Green Version]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
- Edwards, B.J.; Nafar Sefiddashti, M.H.; Khomami, B. Atomistic simulation of shear flow of linear alkane and polyethylene liquids: A 50-year retrospective. J. Rheol. 2022, 66, 415–489. [Google Scholar] [CrossRef]
- Baig, C.; Mavrantzas, V.G.; Kröger, M. Flow effects on melt structure and entanglement network of linear polymers: Results from a nonequilibrium molecular dynamics simulation study of a polyethylene melt in steady shear. Macromolecules 2010, 43, 6886–6902. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Elucidating the molecular rheology of entangled polymeric fluids via comparison of atomistic simulations and model predictions. Macromolecules 2019, 52, 8124–8143. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Evaluation of reptation-based modeling of entangled polymeric fluids including chain rotation via nonequilibrium molecular dynamics simulation. Phys. Rev. Fluids 2017, 2, 083301. [Google Scholar] [CrossRef]
- Edwards, C.N.; Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. In-plane and out-of-plane rotational motion of individual chain molecules in steady shear flow of polymer melts and solutions. J. Mol. Graph. Model. 2018, 81, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Stephanou, P.S.; Edwards, B.; Khomami, B. A mean-field anisotropic diffusion model for unentangled polymeric liquids and semi-dilute solutions: Model development and comparison with experimental and simulation data. J. Non-Newton. Fluid Mech. 2011, 166, 593–606. [Google Scholar] [CrossRef]
- Su, Y.Y.; Khomami, B. Interfacial stability of multilayer viscoelastic fluids in slit and converging channel die geometries. J. Rheol. 1992, 36, 357–387. [Google Scholar] [CrossRef]
- Wilson, G.M.; Khomami, B. An experimental investigation of interfacial instabilities in multilayer flow of viscoelastic fluids. Part II. Elastic and nonlinear effects in incompatible polymer systems. J. Rheol. 1993, 37, 315–339. [Google Scholar] [CrossRef]
- Khomami, B.; Ranjbaran, M.M. Experimental studies of interfacial instabilities in multilayer pressure-driven flow of polymeric melts. Rheol. Acta 1997, 36, 345–366. [Google Scholar] [CrossRef]
- Nieto Simavilla, D.; Español, P.; Ellero, M. Non-affine motion and selection of slip coefficient in constitutive modeling of polymeric solutions using a mixed derivative. J. Rheol. 2022, 67, 253–267. [Google Scholar] [CrossRef]
- Ravindranath, S.; Wang, S.Q. Universal scaling characteristics of stress overshoot in startup shear of entangled polymer solutions. J. Rheol. 2008, 52, 681–695. [Google Scholar] [CrossRef] [Green Version]














| Parameter | Value | Units |
|---|---|---|
| a | 200 | |
| 4.5 | ||
| 3.0 | ||
| 0.012 | ||
| 2.38 (N-1000) and 2.0 (-6) | ||
| 400 |
| Chain Length | |||||
|---|---|---|---|---|---|
| N-1000 in hexadecane | 16 (310) | 4 (84) | 1.5 (31) | 370,000 | 791,380 |
| N-1000 in benzene | 16 (310) | 4 (84) | 1.5 (31) | 240,000 | 590,000 |
| DPD Chain | Z | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| N-1000 in hexadecane | 0.46 | 20 | 62 | 24.5 | 46 | 25 | 234 | ||
| N-1000 in benzene | 0.3 | 15 | 61.33 | 25.2 | 30 | 17 | 236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudaghi, M.; Edwards, B.J.; Khomami, B. Molecular Processes Leading to Shear Banding in Entangled Polymeric Solutions. Polymers 2023, 15, 3264. https://doi.org/10.3390/polym15153264
Boudaghi M, Edwards BJ, Khomami B. Molecular Processes Leading to Shear Banding in Entangled Polymeric Solutions. Polymers. 2023; 15(15):3264. https://doi.org/10.3390/polym15153264
Chicago/Turabian StyleBoudaghi, Mahdi, Brian J. Edwards, and Bamin Khomami. 2023. "Molecular Processes Leading to Shear Banding in Entangled Polymeric Solutions" Polymers 15, no. 15: 3264. https://doi.org/10.3390/polym15153264