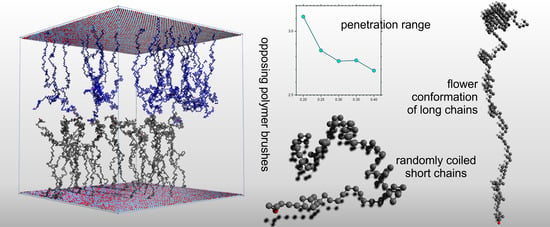
Polymerization and Structure of Opposing Polymer Brushes Studied by Computer Simulations
Abstract
:1. Introduction
2. The Model and Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eisenriegler, E. Polymers Near Surfaces; World Scientific: Singapore, 1993. [Google Scholar]
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Zhao, B.; Brittain, W.J. Polymer brushes: Surface-immobilized macromolecules. Prog. Polym. Sci. 2000, 25, 677–710. [Google Scholar] [CrossRef]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Bockstaller, M.R.; Matyjaszewski, K. Brush-modified materials: Control of molecular architecture, assembly behavior, properties and applications. Prog. Polym. Sci. 2020, 100, 101180. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Dong, H.; Jakubowski, W.; Pietrasik, J.; Kusumo, A. Grafting from surfaces for “everyone”: ARGET ATRP in the presence of air. Langmuir 2007, 23, 4528–4531. [Google Scholar] [CrossRef] [PubMed]
- Matyjaszewski, K.; Miller, P.J.; Shukla, N.; Immaraporn, B.; Gelman, A.; Luokala, B.B.; Silovan, T.M.; Kickelbick, G.; Vallant, T.; Hoffmann, H.; et al. Polymers at interfaces: Using atom transfer radical polymerization in the controlled growth of homopolymers and block copolymers from silicon surfaces in the absence of untethered sacrificial initiator. Macromolecules 1999, 32, 8716–8724. [Google Scholar] [CrossRef]
- Tsuji, Y.; Ohno, K.; Yamamoto, S.; Goto, A.; Fukuda, T. Structure and properties of high-density polymer brushes prepared by surface-initiated living radical polymerization. Adv. Polym. Sci. 2006, 197, 1–45. [Google Scholar]
- Khabibullin, A.; Mastan, E.; Matyjaszewski, K.; Zhu, S. Surface-initiated atom transfer radical polymerization. Adv. Polym. Sci. 2016, 270, 29–76. [Google Scholar]
- Reith, D.; Milchev, A.; Virnau, P.; Binder, K. Computer simulation studies of chain dynamics in polymer brushes. Macromolecules 2012, 45, 4381–4393. [Google Scholar] [CrossRef]
- Deng, B.; Palermo, E.F.; Shi, Y. Comparison of chain-growth polymerization in solution versus on surface using reactive coarse-grained simulations. Polymer 2017, 129, 105–118. [Google Scholar] [CrossRef]
- Elliot, I.G.; Kuhl, T.L.; Faller, R. Molecular simulation study of the structure of high density polymer brushes in good solvent. Macromolecules 2010, 43, 9131–9138. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Malfreyt, P.; Tildesley, D.J. Dissipative Particle Dynamics simulations of grafted polymer chains between two walls. Langmuir 2000, 16, 4732–4740. [Google Scholar] [CrossRef]
- Pakula, T.; Zhulina, E.B. Computer simulations of polymers in thin layers. II. Structure of polymer melt layers consisting of end-to-end grafted chains. J. Chem. Phys. 1991, 95, 4691–4697. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Pakula, T. Structure of dense polymer layers between end-grafting and end-adsorbing walls. Macromolecules 1992, 25, 754–758. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Balazs, A.C. Phase behavior of end-functionalized polymers confined between two surfaces. J. Chem. Phys. 2000, 113, 2479–2483. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers—A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of polymer brushes near the theta point—A Monte Carlo simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Stadler, C.; Schmid, F. Phase behavior of grafted chain molecules: Influence of head size and chain length. J. Chem. Phys. 1999, 110, 9697–9705. [Google Scholar] [CrossRef] [Green Version]
- Stadler, C.; Lange, H.; Schmid, F. Short grafted chains: Monte Carlo simulations of a model for monolayers of amphiphiles. Phys. Rev. E 1999, 59, 4248–4257. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Jiang, W.; Han, S. Dynamic Monte Carlo simulation on the polymer chain with one end grafted on a flat surface. Macromol. Theory Simul. 2001, 10, 339–342. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP—Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Genzer, J. In silico polymerization: Computer simulation of controlled radical polymerization in bulk and on flat surfaces. Macromolecules 2006, 39, 7157–7169. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of controlled radical polymerization: Effect of chain confinement due to initiator grafting density and solvent quality in “grafting from” method. Macromolecules 2010, 43, 9567–9577. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of concurrent bulk- and surface initiated living polymerization. Macromolecules 2012, 45, 2128–2137. [Google Scholar] [CrossRef]
- Jalili, K.; Abbasi, F.; Milchev, A. Dynamic compression of in situ grown living polymer brush: Simulation and experiment. Macromolecules 2012, 45, 9827–9840. [Google Scholar] [CrossRef] [Green Version]
- Milchev, A.; Wittmer, J.P.; Landau, D.P. Formation and equilibrium properties of living polymer brushes. J. Chem. Phys. 2000, 112, 1606–1615. [Google Scholar] [CrossRef] [Green Version]
- Binder, K. Scaling concepts for polymer brushes and their test with computer simulation. Eur. Phys. J. E 2002, 9, 293–298. [Google Scholar] [CrossRef]
- Netz, R.R.; Schick, M. Polymer brushes: From self-consistent field theory to classical theory. Macromolecules 1998, 31, 5105–5122. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V.; Pryamitsyn, V.A.; Birshtein, T.M. Coil globule type transitions in polymers. 1. Collapse of layers of grafted polymer-chains. Macromolecules 1991, 24, 140–149. [Google Scholar] [CrossRef]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Some dynamic properties of grafted polymer layers. Colloids Surf. A Physicochem. Eng. Asp. 1994, 86, 85–89. [Google Scholar] [CrossRef]
- de Vos, W.M.; Leermakers, F.A.M. Modeling the structure of a polydisperse polymer brush. Polymer 2009, 50, 305–316. [Google Scholar] [CrossRef]
- Matsen, M.W. Field theoretic approach for block polymer melts: SCFT and FTS. J. Chem. Phys. 2020, 152, 110901. [Google Scholar] [CrossRef] [Green Version]
- Milner, S.T. Polymer brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Effects of polydispersity in the end-grafted polymer brush. Macromolecules 1989, 22, 853–861. [Google Scholar] [CrossRef]
- Alexander, S. Adsorption of chain molecules with a polar head. A scaling description. J. Phys. 1977, 38, 983–987. [Google Scholar] [CrossRef]
- Yamamoto, S.; Ejaz, M.; Tsujii, Y.; Matsumoto, M.; Fukuda, T. Surface interaction forces of well-defined, high-density polymer brushes studied by Atomic Force Microscopy. 1. Effect of chain length. Macromolecules 2000, 33, 5602–5607. [Google Scholar] [CrossRef]
- Baschnagel, J.; Paul, W.; Tries, V.; Binder, K. Statics and dynamics of bidisperse polymer melt. A Monte Carlo study of the Bond-Fluctuation-Model. Macromolecules 1998, 31, 3856–3867. [Google Scholar] [CrossRef]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479–3501. [Google Scholar] [CrossRef]
- Klushin, L.I.; Skvortsov, A.M.; Qi, S.; Kreer, T.; Schmid, F. Polydispersity effects on interpenetration in compressed brushes. Macromolecules 2019, 52, 1810–1820. [Google Scholar] [CrossRef]
- Galuschko, A.; Spirin, L.; Kreer, T.; Johner, A.; Pastorino, C.; Wittmer, J.; Baschnagel, J. Frictional forces between strongly compressed, nonentangled polymer brushes: Molecular dynamics simulations and scaling theory. Langmuir 2010, 26, 6418–6429. [Google Scholar] [CrossRef] [PubMed]
- Desai, P.R.; Sinha, S.; Das, S. Compression of polymer brushes in the weak interpenetration regime: Scaling theory and molecular dynamics simulations. Soft Matter 2017, 13, 4159–4166. [Google Scholar] [CrossRef] [PubMed]
- Tai, C.-H.; Pan, G.-T.; Yu, H.-Y. Entropic effects in solvent-free bidisperse polymer brushes investigated using Density Functional Theories. Langmuir 2019, 35, 16835–16849. [Google Scholar] [CrossRef] [PubMed]
- Zhulina, E.B.; Rubinstein, M. Lubrication by polyelectrolyte brushes. Macromolecules 2014, 47, 5825–5838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romiszowski, P.; Sikorski, A. Properties of Polymer Sandwich Brushes. Colloids Surf. A Physicochem. Eng. Asp. 2008, 321, 254–257. [Google Scholar] [CrossRef]
- Romiszowski, P.; Sikorski, A. The Monte Carlo Dynamics of Polymer Chains in Sandwich Brushes. Rheol. Acta 2008, 47, 565–569. [Google Scholar] [CrossRef]
- Mendonça, A.; Goujon, F.; Malfreyt, P.; Tildedsley, D.J. Monte Carlo simulations of the static friction between two grafted polymer brushes. Phys. Chem. Chem. Phys. 2016, 18, 6164–6174. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Interaction between grafted polymeric brushes: A molecular-dynamics study. Phys. Rev. Lett. 1989, 63, 1074–1077. [Google Scholar] [CrossRef] [PubMed]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. Frictional forces in polyelectrolyte brushes: Effects of sliding velocity, solvent quality and salt. Soft Matter 2012, 8, 4635–4644. [Google Scholar] [CrossRef]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. The kinetic friction coefficient of neutral and charged polymer brushes. Soft Matter 2013, 9, 2966–2972. [Google Scholar] [CrossRef]
- Hehmeyer, O.J.; Stevens, M.J. Molecular dynamics simulations of grafted polyelectrolytes on two apposing wall. J. Chem. Phys. 2005, 122, 134909. [Google Scholar] [CrossRef] [PubMed]
- Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Dynamics of opposing polymer brushes. A computer simulation study. Polymers 2021, 13, 2758. [Google Scholar] [CrossRef] [PubMed]
- Pakula, T. Simulation on the completely occupied lattices. In Simulation Methods for Polymers; Kotelyanskii, M., Theodorou, D.N., Eds.; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 2004. [Google Scholar]
- Polanowski, P.; Sikorski, A. Simulation of diffusion in a crowded environment. Soft Matter 2014, 10, 3597–3607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, H.; Polanowski, P.; Matyjaszewski, K. Gelation in living copolymerization of monomer and divinyl cross linker: Comparison of ATRP experiments with Monte Carlo simulations. Macromolecules 2009, 42, 5925–5932. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Modeling of branching and gelation in living copolymerization of monomer and divinyl cross-linker using dynamic lattice liquid model (DLL) and Flory–Stockmayer model. Polymer 2010, 51, 6084–6092. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Krysiak, K.; Matyjaszewski, K. Influence of intramolecular crosslinking on gelation in living copolymerization of monomer and divinyl cross-linker. Monte Carlo simulation studies. Polymer 2015, 79, 171–178. [Google Scholar] [CrossRef]
- Kozanecki, M.; Halagan, K.; Saramak, J.; Matyjaszewski, K. Diffusive properties of solvent molecules in the neighborhood of a polymer chain as seen by Monte-Carlo simulations. Soft Matter 2016, 12, 5519–5528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brush relaxation during and after polymerization—Monte Carlo simulation study. Polymer 2019, 173, 190–196. [Google Scholar] [CrossRef]
- Kiełbik, R.; Hałagan, K.; Zatorski, W.; Jung, J.; Ulański, J.; Napieralski, A.; Rudnicki, K.; Amrozik, P.; Jabłoński, G.; Stożek, D.; et al. ARUZ—Large-scale, Massively parallel FPGA-based Analyzer of Real Complex Systems. Comput. Phys. Commun. 2018, 232, 22–34. [Google Scholar] [CrossRef]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Zatorski, K.; Ulański, J.; Napieralski, A.; Pakuła, T. Panel z Układami Elektronicznymi i Zestaw Paneli. PAT.223795, 1 March 2016. [Google Scholar]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Zatorski, K.; Ulański, J.; Napieralski, A.; Pakuła, T. Maszyna Równoległa z Komórkami Operacyjnymi Umieszczonymi w Węzłach Sieci Powierzchniowo Centrowanej. PAT. 227249, 7 June 2017. [Google Scholar]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Hałagan, K.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakuła, T. Maszyna Równoległa ze Zzredukowaną Liczbą Połączeń Pomiędzy Układami Logicznymi. PAT. 227250, 7 June 2017. [Google Scholar]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Hałagan, K.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakuła, T. System of Electronic Modules Having a Redundant Configuration. EP3079066B1, 23 August 2017. [Google Scholar]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Hałagan, K.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakuła, T. A Panel with Electronic Circuits and a Set of Panels. EP3079071B1, 1 August 2018. [Google Scholar]
- Jung, J.; Kiełbik, R.; Hałagan, K.; Polanowski, P.; Sikorski, A. Technology of Real-World Analyzers (TAUR) and its practical application. Comput. Methods Sci. Technol. 2020, 26, 69–75. [Google Scholar]
- Eslami, H.; Gharibi, A.; Müller-Plathe, F. Mechanisms of Nucleation and Solid–Solid-Phase Transitions in Triblock Janus Assemblies. J. Chem. Theory Comput. 2021, 17, 1742–1754. [Google Scholar] [CrossRef] [PubMed]
- Zimm, B.H. Apparatus and methods for measurement and interpenetration of the angular variation of light scattering: Preliminary results on polystyrene solutions. J. Chem. Phys. 1948, 16, 1099–1116. [Google Scholar] [CrossRef]
- Eslami, H.; Rahimi, M.; Müller-Plathe, F. Molecular Dynamics Simulation of a Silica Nanoparticle in Oligomeric Poly(methyl methacrylate): A Model System for Studying the Interphase Thickness in a Polymer–Nanocomposite via Different Properties. Macromolecules 2013, 46, 8680–8692. [Google Scholar] [CrossRef]
- Keshtkar, M.; Mehdipour, N.; Eslami, H. Thermal Conductivity of Polyamide-6,6/Carbon Nanotube Composites: Effects of Tube Diameter and Polymer Linkage between Tubes. Polymers 2019, 11, 1465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teraoka, I. Polymer Solutions. An Introduction to Physical Properties; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Skvortsov, A.M.; Gorbunov, A.A.; Leermakers, F.A.M.; Fleer, G.J. Long minority chains in a polymer brush. A first order adsorption transition. Macromolecules 1999, 32, 2004–2015. [Google Scholar] [CrossRef]
- Kreer, T.; Müser, M.H.; Binder, K.; Klein, J. Frictional drag mechanisms between polymer-bearing surfaces. Langmuir 2001, 17, 7804–7813. [Google Scholar] [CrossRef]
- Ohno, K.; Sakamoto, T.; Minagawa, T.; Okabe, Y. Entropy of polymer brushes in good solvents. A Monte Carlo study. Macromolecules 2007, 40, 723–730. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Polymerization and Structure of Opposing Polymer Brushes Studied by Computer Simulations. Polymers 2021, 13, 4294. https://doi.org/10.3390/polym13244294
Halagan K, Banaszak M, Jung J, Polanowski P, Sikorski A. Polymerization and Structure of Opposing Polymer Brushes Studied by Computer Simulations. Polymers. 2021; 13(24):4294. https://doi.org/10.3390/polym13244294
Chicago/Turabian StyleHalagan, Krzysztof, Michal Banaszak, Jaroslaw Jung, Piotr Polanowski, and Andrzej Sikorski. 2021. "Polymerization and Structure of Opposing Polymer Brushes Studied by Computer Simulations" Polymers 13, no. 24: 4294. https://doi.org/10.3390/polym13244294