Error Analysis of a Spherical Capacitive Sensor for the Micro-Clearance Detection in Spherical Joints
Abstract
:1. Introduction
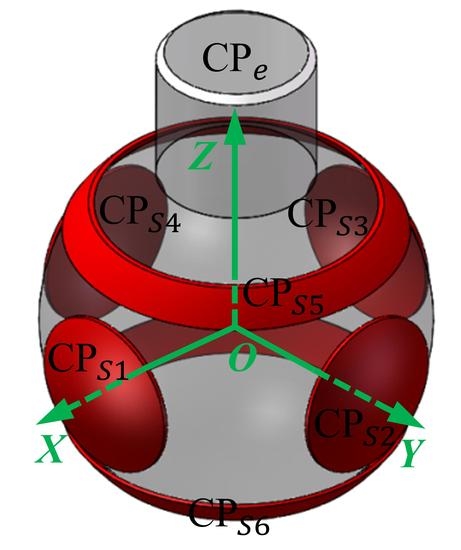
2. Measurement Principle of the Spherical Capacitive Sensor
3. Measurement Error Caused by the Manufacture of the Capacitive Sensor
3.1. Effect of the Ball Shape
3.2. Effect of the Plate Shape
4. Measurement Error Introduced by the Installation of the Capacitive Plates
4.1. Effect of Offset Installation
4.1.1. Axial Offset Installation
4.1.2. Radial Offset Installation
4.2. Effect of Inclined Installation
5. Simulation Setup
6. Results and Discussions
6.1. Effect of the Manufacture Deviation of Spherical Capacitive Sensor
6.1.1. Measurement Error Caused by the Ball Shape
6.1.2. Measurement Error Produced by the Plate Shape
6.2. Effect of the Installation Deviation of Spherical Capacitive Plates
6.2.1. Measurement Error Caused by the Offset Installation
6.2.2. Measurement Error Produced by the Angular Installation
7. Conclusions
- (1)
- If the shape of the ball becomes ellipsoid, the capacitance of the spherical capacitive sensor could change with the rotation of the ball in a spherical joint, which leads to a large attitude error. If the shape error of the ball reaches 10 μm, the attitude error is about 7.7% at the eccentric displacement of ball δx = 40 μm.
- (2)
- The ellipsoidal plate can produce higher-order capacitance errors, variable capacitance errors, and constant capacitance errors. For the shape error of the plate Δr = 10 μm, the total capacitance error is of 15% at the eccentric displacement of ball δx = 40 μm. This mainly comes from the negative constant additional capacitance.
- (3)
- The axial offset of the plate can generate higher-order capacitance errors, variable capacitance errors, and constant capacitance errors. Compared with the ideal position, the differential capacitance for the axial offset of the plate m = 10 μm is reduced by 17.2% at the eccentric displacement of ball δx = 40 μm. This reduction can be mainly ascribed to the negative constant additional capacitance.
- (4)
- If a pair of plates is radial offset and misaligned, a higher-order capacitance error and variable capacitance error are produced. For the radial offset of the plate h = 100 μm, the total capacitance error is of 5.2% at the eccentric displacement of ball δx = 40 μm.
- (5)
- If a pair of plates is radial offset and aligned, only a higher-order capacitance error is produced. At the eccentric displacement of ball δx = 40 μm, the differential capacitance for the radial offset of n = 50 μm is increased by 1.3% compared with that for the ideal position.
- (6)
- The inclined capacitive plate could produce a higher-order capacitance error and variable capacitance error. For the inclined angle of the plate α = 0.2°, the total capacitance error is about 5% at the eccentric displacement of ball δx = 40 μm.
Author Contributions
Funding
Conflicts of Interest
References
- Guckert, M.L.; Naish, M.D. A compact 3 degree of freedom spherical joint. ASME J. Mech. Robot. 2011, 3, 31005. [Google Scholar] [CrossRef]
- Robertson, A.P.; Slocum, A.H. Measurement and characterization of precision spherical joints. Precis. Eng. 2006, 30, 1–12. [Google Scholar] [CrossRef]
- Erkaya, S. Experimental investigation of flexible connection and clearance joint effects on the vibration responses of mechanisms. Mech. Mach. Theory 2018, 121, 515–529. [Google Scholar] [CrossRef]
- Flores, P.; Ambrosio, J.; Claro, J.C.; Lankarani, H.M. Dynamics of multibody systems with spherical clearance joints. J. Comput. Nonlinear Dyn. 2006, 1, 240–247. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Yao, G.; Huang, H. Dynamic Analysis of a spatial mechanism including frictionless spherical clearance joint with flexible socket. J. Comput. Nonlinear Dyn. 2018, 13, 0310023. [Google Scholar] [CrossRef]
- Chen, X.L.; Gao, W.H.; Deng, Y.; Wang, Q. Chaotic characteristic analysis of spatial parallel mechanism with clearance in spherical joint. Nonlinear Dyn. 2018, 94, 2625–2642. [Google Scholar] [CrossRef]
- Li, X.; Ding, X.; Chirikjian, G.S. Analysis of angular-error uncertainty in planar multiple-loop structures with joint clearances. Mech. Mach. Theory 2015, 91, 69–85. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Muvengei, O.; Kihiu, J.; Ikua, B. Dynamic analysis of planar rigid-body mechanical systems with two-clearance revolute joints. Nonlinear Dyn. 2013, 73, 259–273. [Google Scholar] [CrossRef]
- Erkaya, S. Effects of joint clearance on the motion accuracy of robotic manipulators. J. Mech. Eng. 2018, 64, 82–94. [Google Scholar]
- Varedi-Koulaei, S.M.; Daniali, H.M.; Farajtabar, M.; Fathi, B.; Shafiee-Ashtiani, M. Reducing the undesirable effects of joint clearance on the behavior of the planar 3-RRR parallel manipulators. Nonlinear Dyn. 2016, 86, 1007–1022. [Google Scholar] [CrossRef]
- Ahn, H.-J.; Han, D.C. Optimal multi-segment cylindrical capacitive sensor. Meas. Sci. Technol. 2003, 14, 531–542. [Google Scholar] [CrossRef]
- George, B.; Tan, Z.; Nihtianov, S. Advances in capacitive, eddy current, and magnetic displacement sensors and corresponding interfaces. IEEE Trans. Ind. Electron. 2017, 64, 9595–9607. [Google Scholar] [CrossRef]
- Ripka, P.; Janosek, M. Advances in magnetic field sensors. IEEE Sens. J. 2010, 10, 1108–1116. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.K.; Wang, R.B.; Deng, Z.Y.; Kang, Y.H. A displacement sensing method based on alternating current magnetic flux measurement. Meas. Sci. Technol. 2018, 29, 085010. [Google Scholar] [CrossRef]
- Zhang, J.; Duan, F.; Niu, G.; Jiang, J.; Li, J. A blade tip timing method based on a microwave sensor. Sensors 2017, 17, 1097. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.K.; Chen, I.M.; Yan, L.; Luo, Z. A novel approach for positional sensing of a spherical geometry. Sens. Actuators A Phys. 2011, 168, 328–334. [Google Scholar] [CrossRef]
- Han, Y.; Zhong, C.; Zhu, X.; Zhe, J. Online monitoring of dynamic tip clearance of turbine blades in high temperature environments. Meas. Sci. Technol. 2018, 29, 045102. [Google Scholar] [CrossRef] [Green Version]
- Nabavi, M.R.; Nihtianov, S.N. Design strategies for eddy-current displacement sensor systems: Review and recommendations. IEEE Sens. J. 2012, 12, 3346–3355. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Ueda, M. An active sensor for monitoring bearing wear by means of an eddy current displacement sensor. Meas. Sci. Technol. 2007, 18, 311–317. [Google Scholar] [CrossRef]
- Wang, W.; Yang, H.; Zhang, M.; Chen, Z.F.; Shi, G.; Lu, K.Q.; Xiang, K.; Ju, B.F. A novel approach for detecting rotational angles of a precision spherical joint based on a capacitive sensor. Micromachines 2019, 10, 280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, W.; Wen, Y.H.; Yu, J.P.; Chen, Z. Impact of fringe effect on measuring accuracy of planar capacitive sensor. Sens. Lett. 2011, 9, 1458–1461. [Google Scholar] [CrossRef]
- Yu, Z.C.; Peng, K.; Liu, X.K.; Chen, Z.R.; Huang, Y. A high-precision absolute angular-displacement capacitive sensor using three-stage time-grating in conjunction with a remodulation scheme. IEEE Trans. Ind. Electron. 2019, 66, 7376–7385. [Google Scholar] [CrossRef]
- Peng, K.; Yu, Z.C.; Liu, X.K.; Chen, Z.R.; Pu, H.J. Features of capacitive displacement sensing that provide high-accuracy measurements with reduced manufacturing precision. IEEE Trans. Ind. Electron. 2017, 64, 7377–7386. [Google Scholar] [CrossRef]
- Zhang, D.D.; Zhao, S.J.; Zheng, Q.S.; Lin, L. Absolute capacitive grating displacement measuring system with both high-precision and long-range. Sens. Actuators A Phys. 2019, 295, 11–22. [Google Scholar] [CrossRef]
- Ahn, H.-J. A cylindrical capacitive sensor (CCS) for both radial and axial motion measurements. Meas. Sci. Technol. 2006, 17, 2027–2034. [Google Scholar] [CrossRef]
- Anandan, N.; George, B. A wide-range capacitive sensor for linear and angular displacement measurement. IEEE Trans. Ind. Electron. 2017, 64, 5728–5737. [Google Scholar] [CrossRef]
- Hu, P.H.; Lu, Y.C.; Chen, S.Y.; Hu, Y.; Zhu, L.Q. Measurement method of rotation angle and clearance in intelligent spherical hinge. Meas. Sci. Technol. 2018, 29, 64012. [Google Scholar] [CrossRef]
- Wang, W.; Yang, H.; Zhang, M.; Chen, Z.F.; Shi, G.; Lu, K.Q.; Xiang, K.; Ju, B.F. A novel method for the micro-clearance measurement of a precision spherical joint based on a spherical differential capacitive sensor. Sensors 2018, 18, 3366. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Qiu, W.J.; Yang, H.; Wu, H.M.; Shi, G.; Chen, Z.F.; Lu, K.Q.; Xiang, K.; Ju, B.F. An improved capacitive sensor for detecting the micro-clearance of spherical joints. Sensors 2019, 19, 2694. [Google Scholar] [CrossRef] [Green Version]



















| Parameters of Spherical Capacitive Sensor | Value |
|---|---|
| Central angle of CPS1 ~ CPS4 Central angle of CPS5 and CPS6 | 0°~30° |
| 35°~45° | |
| Inner radius of spherical capacitive plate (R) | 25 mm |
| Radius of the ball (r) | 24.8 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Qiu, W.; Yang, H.; Lu, K.; Chen, Z.; Ju, B. Error Analysis of a Spherical Capacitive Sensor for the Micro-Clearance Detection in Spherical Joints. Micromachines 2020, 11, 837. https://doi.org/10.3390/mi11090837
Wang W, Qiu W, Yang H, Lu K, Chen Z, Ju B. Error Analysis of a Spherical Capacitive Sensor for the Micro-Clearance Detection in Spherical Joints. Micromachines. 2020; 11(9):837. https://doi.org/10.3390/mi11090837
Chicago/Turabian StyleWang, Wen, Wenjun Qiu, He Yang, Keqing Lu, Zhanfeng Chen, and Bingfeng Ju. 2020. "Error Analysis of a Spherical Capacitive Sensor for the Micro-Clearance Detection in Spherical Joints" Micromachines 11, no. 9: 837. https://doi.org/10.3390/mi11090837