Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors
Abstract
:1. Introduction
- 1.
- Starting from some iteration, the number of which is less than N, the value of the minimized functional becomes comparable to the background of rounding errors. This means that all subsequent iterations are meaningless and the iterative process can be stopped, because the value of the functional will not decrease at subsequent iterations. Knowing such an iteration number makes it possible to interrupt calculations and save computational resources by finding an approximate solution by performing a much smaller number of operations compared to direct solution methods.
- 2.
- In the first case, it is also possible that the execution of the full set of N iterations leads to “destruction” of the numerical solution. Thus, the possibility of early termination of the iterative process can be especially useful in solving applied problems. The implementation of this possibility in practice not only saves computational resources, but also makes it possible to find an adequate approximate solution.
- 3.
- Due to the influence of rounding errors on the accuracy of determining the minimization directions and steps along them, after performing N iterations, the value of the minimized functional remains sufficiently large. This means that the approximate solution found after N iterations can be refined further if the iterative process is continued. In this case, the iterative process must be continued until the value of the functional reaches the background of rounding errors.
2. Sequential Algorithm and Its Software Implementation
2.1. Classical Implementation of the Conjugate Gradient Method
| Algorithm 1: Pseudocode for a sequential version of the “classical” algorithm |
 |
| Listing 1. The Python code for a sequential version of the “classical” algorithm. |
|
2.2. Improved Implementation of the Conjugate Gradient Method
- 1.
- The function returns (1) the array x that contains the solution of System (1) found by the improved Algorithm 2, (2) the number of iterations s that needed to be done by the algorithm to find an approximate solution, (3) the array x_classic, which contains the solution found using the “classical” Algorithm 1 (this array contains such a solution only if the number of iterations performed by the algorithm ).
- 2.
- This implementation (and the corresponding pseudocode) takes into account that the result of each dot product is used twice, so the result of the dot product is stored in a separate variable.
- 3.
- At the first iteration of the algorithm (), the value of is calculated using the commandsigma2_r = dot(A.T**2, dot(A**2, x**2) + b**2)A feature of Python is that under the arrays A**2 and A.T**2, which contain the matrices and , a separate memory space is allocated. This is very bad, because it is assumed that problem (1) is being solved with a huge matrix A.
| Algorithm 2: Pseudocode for a sequential version of the improved algorithm |
 |
| Listing 2. The Python code for a sequential version of the improved algorithm. |
|
- sigma2_r = dot_special(A.T, dot_special(A,x**2,M,N)+b**2, N, M)
- from numba import jit,prange
- @jit(nopython=True, parallel=True)
- def dot_special(A, x, M, N):
- b = empty(M)
- for m in prange(M):
- b[m] = 0.
- for n in range(N):
- b[m] = b[m] + A[m, n]**2*x[n]
- return b
- sigma2_r = zeros(N)
2.3. An Example of How the Algorithm Works
3. Approaches to Building a Parallel Algorithm and Its Software Implementation
3.1. Parallelizable Operations
- 1.
- The scalar product of two vectors of dimension N.This operation requires N multiplications and additions—for a total of arithmetic operations. It is customary to denote , which indicates the linear computational complexity of the scalar product operation.
- 2.
- Multiplication of a matrix of dimension by a vector of dimension N.To obtain each element of the final vector, it is necessary to scalarly multiply the corresponding row of the A matrix by the multiplied vector. Such calculations must be carried out for each element of the vector, which is the result of multiplication. Thus, arithmetic operations must be performed in total. In the case of a square matrix (), there will be of such operations, which indicates the quadratic computational complexity of the operation of multiplying a matrix by a vector.
- 3.
- Multiplication of a transposed matrix of dimension by a vector of dimension M.The computational complexity of this operation is equivalent to the operation of multiplying a matrix by a vector.
- 4.
- Addition of two vectors of dimension N.This operation requires N additions. That is, the computational complexity of this operation is linear.
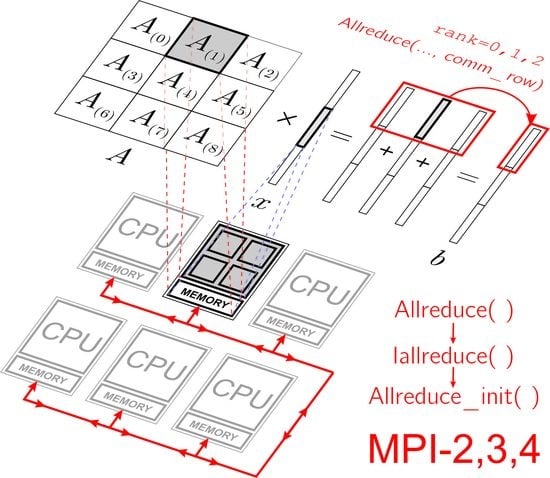
3.2. Distribution of Data by MPI Processes Participating in Computations
3.3. Parallel Algorithm for Matrix–Vector Multiplication in the Case of Two-Dimensional Division of the Matrix into Blocks
- 1.
- Each process should store not the whole vector x, but only a part of this vector. The vector will have to be sent not to all processes of the comm communicator, but only to a part of the processes of this communicator—to the processes of the column with index n of the process grid. In this case, the transfer of data among the processes of each column of the process grid can be organized in parallel with the transfer of data among the processes of other columns of the grid of processes, which will give a gain in time.
- 2.
- When calculating part of the final vector b, it is necessary to exchange messages not to all processes of the comm communicator, but only to part of the processes of this communicator—to the processes of the line with index m of the introduced grid of processes. In this case, the data transfer along each line of the process grid can be organized in parallel with the transfer of data among the processes of other lines of the process grid, which will also give a gain in time.
- comm_col = comm.Split(rank % num_col, rank)
- comm_row = comm.Split(rank // num_col, rank)
- b_part_temp = dot(A_part, x_part)
- b_part = empty(M_part, dtype=float64)
- comm_row.Allreduce([b_part_temp, M_part, MPI.DOUBLE],
- [b_part, M_part, MPI.DOUBLE], op=MPI.SUM)
3.4. A Parallel Algorithm for Multiplying a Transposed Matrix by a Vector in the Case of Two-Dimensional Division of a Matrix into Blocks
- 1.
- Each process should store not the whole vector b, but only a part of this vector. The vector will have to be sent not to all the processes of the communicator comm, but only to a part of the processes of this communicator—to the processes of the row with index m of the process grid. In this case, the transfer of data among the processes of each row of the process grid can be organized in parallel with the transfer of data among the processes of other rows of the grid of processes, which will give a gain in time.
- 2.
- When calculating the part of the final vector x, it is necessary to exchange messages not with all processes of the communicator comm, but only with part of the processes of this communicator—with the processes of the column with index n of the introduced grid of processes. In this case, the data transfer along each column of the process grid can be organized in parallel with the transfer of data among the processes of other columns of the process grid, which will also give a gain in time.
- x_part_temp = dot(A_part.T, b_part)
- x_part = empty(N_part, dtype=float64)
- comm_col.Allreduce([x_part_temp, N_part, MPI.DOUBLE],
- [x_part, N_part, MPI.DOUBLE], op=MPI.SUM)
3.5. Parallel Algorithm for Scalar Multiplication of Vectors
- scalar_product_temp = array(dot(r_part, r_part), dtype=float64)
- scalar_product = array(0, dtype=float64)
- comm_row.Allreduce([scalar_product_temp, 1, MPI.DOUBLE],
- [scalar_product, 1, MPI.DOUBLE], op=MPI.SUM)
4. Parallel Version of the Improved Algorithm and Its Software Implementation
4.1. Taking into Account the Capabilities of the Standard MPI-2
4.2. Taking into Account the Capabilities of the Standard MPI-3
| Algorithm 3: Pseudocode for a (“naive”) parallel version of the improved algorithm |
 |
| Listing 3. The Python code for a (“naive”) parallel version of the improved algorithm. |
|
| Algorithm 4: Pseudocode for an efficient parallel version of the improved algorithm |
 |
| Listing 4. The Python code for an efficient parallel version of the improved algorithm. |
|
4.3. Taking into Account the Capabilities of the Standard MPI-4
- 1.
- Before the main loop while, it is necessary to form persistent communication request using MPI functions of the form request[] = Allreduce_init() for all functions of collective interaction of processes Allreduce() and Iallreduce() that occur inside the loop.Remark 6.The arguments to these functions are numpy arrays, namely the fixed memory areas associated with these arrays. When initializing the persistent communication request, all data will be taken/written to these memory areas, which are fixed once when the corresponding persistent request is generated. Therefore, it is necessary to first allocate space in memory for all arrays that are arguments to these functions and, during subsequent calculations, ensure that the corresponding results of the calculations are stored in the correct memory areas.
- 2.
- Inside the while loop, replace the MPI function Allreduce() with the sequence of MPI functions Start(request[]) “+” Wait(request[]).
- 3.
- Inside the while loop, replace the MPI function Iallreduce() with the MPI function Start(request[]).
| Listing 5. The Python code for an efficient parallel version of the improved algorithm with using the MPI-4.0 standart |
|
5. Estimation of the Efficiency and Scalability of a Software Implementation of the Parallel Algorithm
5.1. Description of the Test Example
- comm_cart = comm.Create_cart(dims=(num_row, num_col),
- periods=(True, True),
- reorder=True)
5.2. Scalability: Strong and Weak Scaling
6. Discussion
- 1.
- All program examples are built in such a way that they can be easily rewritten using the C/C++/Fortran programming languages. This is due to the fact that all MPI functions used in Python software implementations use a syntax equivalent to the syntax of the corresponding MPI functions in the C/C++/Fortran programming languages.
- 2.
- If there are GPUs on the computing nodes, the programs can be easily modified by replacing the main calculations using the function dot() from the package numpy with calculations using a similar function from the package cupy, which will allow for the use of GPUs for calculations. Thus, it is easy to use MPI+OpenMP+CUDA hybrid parallel programming technologies. Due to the fact that changes in the software implementation will be quite simple, the program code is not shown here.
- 3.
- The algorithm is primarily designed to solve systems of linear equations with a dense matrix. It has not been tested for solving systems of linear equations with a sparse matrix. Due to the technical features of working with sparse matrices, it is possible that the results regarding the efficiency of software implementation may differ significantly (both for better and for worse). More research is required on this issue.
- 4.
- If System (1) is ill-conditioned, then regularizing algorithms are usually used to solve it [29]. One of the important stages in the application of regularizing algorithms is the stage of choosing the regularization parameter, which must be consistent with the error in specifying the input data and the measure of inconsistency of the system being solved. The considered algorithm makes it possible to accurately estimate the measure of incompatibility of the system being solved.
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Demmel, J.W.; Heath, M.T.; Van Der Vorst, H.A. Parallel numerical linear algebra. Acta Numer. 1993, 2, 111–197. [Google Scholar] [CrossRef] [Green Version]
- Hestenes, M.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 409. [Google Scholar] [CrossRef]
- Greenbaum, A. Iterative Methods For Solving Linear Systems; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Kabanikhin, S. Inverse and Ill-Posed Problems: Theory and Applications; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Woźniakowski, H. Roundoff-error analysis of a new class of conjugate-gradient algorithms. Linear Algebra Its Appl. 1980, 29, 507–529. [Google Scholar] [CrossRef] [Green Version]
- Kaasschieter, E.F. A practical termination criterion for the conjugate gradient method. BIT Numer. Math. 1988, 28, 308–322. [Google Scholar] [CrossRef]
- Strakoš, Z. On the real convergence rate of the conjugate gradient method. Linear Algebra Its Appl. 1991, 154, 535–549. [Google Scholar] [CrossRef] [Green Version]
- Arioli, M.; Duff, I.; Ruiz, D. Stopping Criteria for Iterative Solvers. SIAM J. Matrix Anal. Appl. 1992, 13, 138–144. [Google Scholar] [CrossRef]
- Notay, Y. On the convergence rate of the conjugate gradients in presence of rounding errors. Numer. Math. 1993, 65, 301–317. [Google Scholar] [CrossRef]
- Axelsson, O.; Kaporin, I. Error norm estimation and stopping criteria in preconditioned conjugate gradient iterations. Numer. Linear Algebra Appl. 2001, 8, 265–286. [Google Scholar] [CrossRef] [Green Version]
- Arioli, M.; Noulard, E.; Russo, A. Stopping criteria for iterative methods: Applications to PDE’s. Calcolo 2001, 38, 97–112. [Google Scholar] [CrossRef]
- Strakoš, Z.; Tichỳ, P. On error estimation in the conjugate gradient method and why it works in finite precision computations. Electron. Trans. Numer. Anal. 2002, 13, 56–80. [Google Scholar]
- Arioli, M. A stopping criterion for the conjugate gradient algorithm in a finite element method framework. Numer. Math. 2004, 97, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Meurant, G. The Lanczos and Conjugate Gradient Algorithms: From Theory to Finite Precision Computations; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Chang, X.W.; Paige, C.C.; Titley-Peloquin, D. Stopping Criteria for the Iterative Solution of Linear Least Squares Problems. SIAM J. Matrix Anal. Appl. 2009, 31, 831–852. [Google Scholar] [CrossRef] [Green Version]
- Jiránek, P.; Strakoš, Z.; Vohralík, M. A posteriori error estimates including algebraic error and stopping criteria for iterative solvers. SIAM J. Sci. Comput. 2010, 32, 1567–1590. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.; Loli Piccolomini, E.; Tomba, I. A stopping criterion for iterative regularization methods. Appl. Numer. Math. 2016, 106, 53–68. [Google Scholar] [CrossRef]
- Rao, K.; Malan, P.; Perot, J.B. A stopping criterion for the iterative solution of partial differential equations. J. Comput. Phys. 2018, 352, 265–284. [Google Scholar] [CrossRef]
- Carson, E.C.; Rozložník, M.; Strakoš, Z.; Tichý, P.; Tůma, M. The Numerical Stability Analysis of Pipelined Conjugate Gradient Methods: Historical Context and Methodology. SIAM J. Sci. Comput. 2018, 40, A3549–A3580. [Google Scholar] [CrossRef]
- Cools, S.; Yetkin, E.F.; Agullo, E.; Giraud, L.; Vanroose, W. Analyzing the effect of local rounding error propagation on the maximal attainable accuracy of the pipelined conjugate gradient method. SIAM J. Matrix Anal. Appl. 2018, 39, 426–450. [Google Scholar] [CrossRef] [Green Version]
- Greenbaum, A.; Liu, H.; Chen, T. On the Convergence Rate of Variants of the Conjugate Gradient Algorithm in Finite Precision Arithmetic. SIAM J. Sci. Comput. 2021, 43, S496–S515. [Google Scholar] [CrossRef]
- Polyak, B.; Kuruzov, I.; Stonyakin, F. Stopping Rules for Gradient Methods for Non-Convex Problems with Additive Noise in Gradient. arXiv 2022, arXiv:2205.07544. [Google Scholar]
- Lukyanenko, D.; Shinkarev, V.; Yagola, A. Accounting for round-off errors when using gradient minimization methods. Algorithms 2022, 15, 324. [Google Scholar] [CrossRef]
- De Sturler, E.; van der Vorst, H.A. Reducing the effect of global communication in GMRES(m) and CG on parallel distributed memory computers. Appl. Numer. Math. 1995, 18, 441–459. [Google Scholar] [CrossRef]
- Eller, P.R.; Gropp, W. Scalable non-blocking preconditioned conjugate gradient methods. In Proceedings of the SC’16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 13–18 November 2016; pp. 204–215. [Google Scholar] [CrossRef]
- DAzevedo, E.; Romine, C. Reducing Communication Costs in the Conjugate Gradient Algorithm on Distributed Memory Multiprocessors; Technical Report; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1992. [Google Scholar]
- Dongarra, J.J.; Duff, I.S.; Sorensen, D.C.; Van der Vorst, H.A. Numerical Linear Algebra for High-Performance Computers; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Voevodin, V.; Antonov, A.; Nikitenko, D.; Shvets, P.; Sobolev, S.; Sidorov, I.; Stefanov, K.; Voevodin, V.; Zhumatiy, S. Supercomputer Lomonosov-2: Large Scale, Deep Monitoring and Fine Analytics for the User Community. Supercomput. Front. Innov. 2019, 6, 4–11. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.; Goncharsky, A.; Stepanov, V.; Yagola, A. Numerical Methods for the Solution of Ill-Posed Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukyanenko, D. Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors. Algorithms 2023, 16, 242. https://doi.org/10.3390/a16050242
Lukyanenko D. Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors. Algorithms. 2023; 16(5):242. https://doi.org/10.3390/a16050242
Chicago/Turabian StyleLukyanenko, Dmitry. 2023. "Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors" Algorithms 16, no. 5: 242. https://doi.org/10.3390/a16050242