Prediction-Driven Sequential Optimization for Refined Oil Production-Sales-Stock Decision-Making

Abstract

This paper proposes a prediction-driven sequential optimization methodology for joint decision-making problems of production-sales-stock in refined oil enterprises. In the proposed prediction-driven sequential optimization methodology, three dynamic nonlinear programming models are first constructed to model the production-sales-stock decision-making problems in refined oil enterprises. Then, the analytical solutions to sequential optimization for production-sales-stock decision-making issues are presented by using the inverse inference method in dynamic programming. Finally, the impact of price and demand prediction of refined oil products on sequential optimization for production-sales-stock decision-making are analyzed using a numerical analysis method. Numerical results demonstrated the significant impact of forecasting results of price and demand of refined oil products on sequential optimization decision-making, indicating that the prediction-driven sequential optimization methodology can be used as an effective tool for joint decision-making of production-sales-stock.

1. Introduction

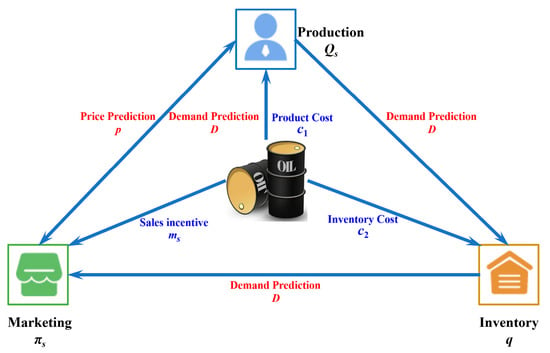
With the continuous opening-up of the refined oil market and the increasing competition among refined oil enterprises in China, optimization of the production-sales-stock decision-making of refined oil products has become a main task of refined oil enterprises. In the context of the gradual opening up of the refined oil market, the economic activities associated with the production, sales, and inventory management of refined oil products are constantly changing, with high complexity and uncertainty. In order to reduce the risk of decision-making, improve the scientific level of management, and enhance the predictability of future situations, it is necessary to adopt scientific methods for prediction and use the accurate prediction results to make the right decisions. As is known to all, forecasting and decision-making are two important components of management. The key to management activities is decision-making and the premise of decision-making is forecasting. Therefore, only by making accurate predictions about the changes of the market demand and price of refined oil products, understanding the market supply and demand situation, and grasping the development direction and trend of the market in a timely manner can managers adjust their competition strategy and inventory scale in terms of the market demand and achieve economic benefits in fierce market competition.

In the existing literature, there are numerous relevant studies on production, marketing, and inventory decision-making in the area of logistics and supply chain management. However, most existing studies have only analyzed one or two aspects of the above three issues (i.e., production, marketing, and inventory decision-making issues), as shown in the literature review. Few researchers have investigated the joint optimization of production, marketing, and inventory decision-making issues from a micro-perspective due to data availability and the difficulties of the multi-objective optimization issues. Therefore, the main goal of this paper is to focus on the joint optimization solution of production-sales-stock decision-making and to construct a joint optimization model of production, marketing, and inventory decision-making from a micro-perspective.

Joint optimization methods are divided into two types: sequential optimization and simultaneous optimization or integrated optimization [1]. In this paper, the sequential optimization method of production, marketing, and inventory decision making will be investigated thoroughly. Different from the previous sequential optimization methods of production-sales-stock decision-making, this paper tries to construct a prediction-driven sequential optimization model for production-sales-stock decision-making by combining the prediction results of market demand and the price of refined oil products.

The main contributions of this paper are two-fold. On the one hand, this paper proposes a novel prediction-driven sequential optimization model and gives a feasible solution to joint optimization of production-sales-stock decision-making. On the other hand, this paper investigates the impact of market demand and price prediction on sequential optimization decision-making, demonstrating the significant effect of prediction on decision-making issue.

The rest of this paper is organized as follows. Section 2 presents a comprehensive literature review. Section 3 constructs a prediction-driven sequential optimization model. Section 4 gives a solution to the constructed sequential optimization model for production-sales-stock decision-making problem. In Section 5, the impacts of demand and price prediction on sequential optimization decision-making are analyzed in detail, while conclusions are drawn in Section 6.

2. Literature Review

In the existing literature, there are many studies on production, marketing, and inventory decision-making. For example, in production decision-making, Zhong et al. [2] proposed a real-time advanced production and scheduling plan based on radio frequency identification (RFID) technology to coordinate different decision-makers in the production process and leverage a data model based on Extensible Markup Language (XML) to enable the deployment and use of the system. Chien et al. [3] presented an uncertain multi-objective decision-making framework for capacity planning that minimizes loss from overcapacity or shortages caused by uncertainty, and empirical analysis confirmed the practical feasibility of this framework. Tsai and Jhong [4] use the activity-based costing (ABC) and constraint theory, combined with the Green Production Decision Model (GPDM), to effectively track related costs to solve the problems of worker shortages and slow production, and to make recommendations for environmental improvement. Wang et al. [5] investigated the optimal production decision-making problems of two competitive supply chains from the perspective of the green supply chain. Experimental results showed that the intensity of competition between supply chains was negatively correlated with wholesale prices and competition between supply chains had a significant impact on the greenness of decision-making scenarios. Rodríguez et al. [6] proposed a fuzzy logic decision-making system based on machine learning that provides decision-making for the operation of production plants to meet production targets where uncertainty exists. Canonico [7] examined how knowledge visualization translates specific multi-objective decision-making issues into production decision optimization problems in the context of partnerships between universities and large automotive companies, and empirically established multi-objective decision-making models as solutions to portfolio optimization problems to improve production quality in factories. In summary, from the perspective of refined oil production enterprises, the prediction of market demand and market price is the premise of production decision-making, and thus the three issues, i.e., market demand prediction, product price forecasting, and production decision-making, should be combined to formulate an optimal business strategy. However, in the existing literature, most scholars have studied these three issues separately or considered only two of them simultaneously, while there is no literature investigating prediction-driven production decision-making problems based on the prediction results of market demand and market price.

For marketing decision-making, Seifert et al. [8] analyzed the integration of direct and indirect marketing channels under decentralized decision-making from a supply chain perspective and explored how to coordinate the supply chain and distribute supply chain profits between manufacturers and their retail channel partners. Berger et al. [9] investigated the impact of negative news on corporate sales. Different from the traditional concept that negative news has only negative effects, their study showed that negative information about a product might increase sales of such products, and enterprises could flexibly use negative news to develop appropriate sales strategies. Rad et al. [10] established an integrated supplier-buyer supply chain model in the event of incomplete production and shortage and investigated the supply chain joint sales strategy. Empirical results showed that coordination and stock-outs could improve the overall expected profit of the system. Yang et al. [11] studied the use of big data technology for promotion by companies with new product sales, and found that the application of big data technology could increase sales and increase the price of new products. In summary, in the perspective of sales decision-making, most of the literature on sales decision-making focuses on the analysis of decision-making behavior, the construction of decision support systems, and the construction and solution of pricing decision models. However, the existing references lack the connection between demand forecasting and sales decisions, and these studies does not jointly optimize and analyze future market demand with sales decision-making for production enterprise.

In the field of inventory control and stock decision-making, Escudero et al. [12] constructed a CORO model in an uncertain environment to simulate the optimization of oil supply, transportation, and distribution in the oil supply chain. Kulp [13] proposed a newsboy model for making inventory decisions for supply chains and manufacturers based on the analysis of corporate relationships. Netessine and Rudi [14] proposed a method of combining order assembly and manufacturing by comparing the advantages and disadvantages of various supply chain inventory management models, considering the cost, flexibility, and warehousing characteristics of manufacturing enterprises. Their method enables upstream and downstream enterprises in the supply chain to share inventory information, thus reducing the risk of supply and demand imbalance due to the bullwhip effect. Caro and Gallien [15] studied stock management issues for fast-selling products, while Zong et al. [16] discussed inventory management and the design of algorithms based on ERP systems. Chan and Prakash [17] examined the issue of inventory collaboration in the supply chain of manufacturing companies using retention costs, deferred costs, and order costs. Raviv and Kolka [18] proposed an inventory model for bicycle rental station management and gave a solution to the model. Experimental results found that the proposed model was suitable for other similar closed-loop inventory systems. Natarajan and Smileinathan [19] studied inventory management problems with financial constraints within limited planning periods. They designed a multi-period stochastic inventory model with financial constraints and demonstrated the effectiveness of optimal replenishment strategies. Moradi and MirHassani [20] analyzed multi-product pipelines to solve the scheduling problem of petroleum derivatives. Their method could meet the day-to-day needs of customers by considering integrated inventory management in distribution centers (DCs) and refineries. Ali et al. [21] provided oil and gas companies with a new way to invest less in inventory planning and maintain plant productivity. Real-world operational practices demonstrated the superiority of this approach. Mishra et al. [22] used a nonlinear price-demand model to develop a sustainable inventory management scheme with carbon emissions restrictions and tax regulations for enterprises, and found that this scheme could enable companies to achieve higher profits under restricted conditions. In summary, the inventory decision in the existing literature focused on inventory cost control, and lacked joint optimization analysis of production, sales, and inventory from the perspective of supply chains.

From the above literature, it can be seen that there are a great many studies about production, sales, and inventory decision-making problem. However, most references only consider these three issues (i.e., production, sales, and inventory) separately or consider only two of them simultaneously, and there is no literature investigating the joint optimization of the three issues simultaneously. Furthermore, some existing joint optimization methods do not take the prediction results of market demand and price change into account, thus leading to decision results that cannot satisfy practical needs. Therefore, this paper proposes a novel prediction-driven joint optimization method for production-sales-stock decision-making problems based on the prediction results of market demand and market price, which will be elaborated below.

3. Prediction-Driven Sequential Optimization Model Construction for Production-Sales-Stock Decision-Making

3.1. Model Settings

Consider a refined oil enterprise that dominates the market and maximizes the expected profit of the enterprise by producing, stocking, and selling certain refined oil products. Assume that the enterprise is faced with a decision-making problem with n periods; without loss of generality, it is only necessary to analyze the decision-making problems of any period of the enterprise (such as the ith period). Usually, the enterprise in period i ($i\in \left\{1,2,\dots ,n\right\}$) faces uncertain product prices and market demand. Therefore, we can assume that the prediction value of the average price of refined oil products during the future period T (i.e., the total duration of period i) is p (p > 0) and the average error of the product price prediction is ${\epsilon }_1$. Meantime, the forecast value of market demand in the future T period is set to D (D > 0) and the average error of the market demand forecast is ${\epsilon }_2$. Note that the prediction errors ${\epsilon }_1$ and ${\epsilon }_2$ indicate the reliability of prediction results.

Suppose that the enterprise first produces refined oil products; the production quantity is $Q_s$ (subscript s is the label of sequential decision-making and the same below). Then, the refined oil products are distributed and stored to oil depots close to the consumer market and sold to outside consumers through oil depots. Since the distribution cost is a one-time fixed cost, the distribution cost can be standardized to zero [23]. Similarly, the delivery time (i.e., the interval between the start of distribution and the arrival of the refined oil products) is also a fixed constant, so it is also normalized to zero. Here, the unit production cost of the finished oil is set to $c_1$ ($c_1>0$). In a certain oil depot, the storage cost per unit of refined oil products per unit of time is $c_2$ ($c_2>0$). At the beginning of the ith period, the amount of residual oil in the oil depot is set to $q$ (this residual oil quantity comes from the (i − 1)th period sales surplus). Thus, the refined oil enterprise needs to replenish the inventory for the oil depot at the time $t_s$ ($0\le t_s\le T$), and the amount of replenishment is equal to the production quantity $Q_s$. It is worth noting that customers or consumers will turn to other small refineries to meet the demand for refined oil products if the oil depot is short of refined oil products. That is, the refined oil shortage will lead to loss of demand during the refined oil shortage period. Because enterprises need to trade off out-of-stock losses and inventory costs, oil depots can allow for being out-of-stock.

In addition, the enterprise can motivate employees to put in sales efforts to increase sales of refined oil products and thus increase market share. The sales of refined oil products gained through incentives is set to $2\sqrt{m_s}$ [24,25], where $m_s$ ($m_s>0$) is the amount of incentives paid. This means that sales incentives can increase the sales amount, but this increase is diminishes marginally. Therefore, the market demand faced by refined the oil enterprise in the T-period are $D+{\epsilon }_2+2\sqrt{m_s}$. For the convenience of analysis, these market demands are set to be generated evenly over the T period. Generally, the chronological order of sequential optimization decision-making is shown below.

Stage 1: The enterprise decides on the amount of sales incentives $m_s$;

Stage 2: The enterprise decides on the production quantity of refined oil products $Q_s$;

Stage 3: The enterprise decides on the replenishment time $t_s$ when the oil depot will replenish its inventory.

For convenience of computation, the mathematical symbols used in this paper are listed in

Table 1. A list of mathematical symbols.

Symbol	Description
$D$	Prediction value of market demand for refined oil products in the ith period
${\epsilon }_2$	Prediction error of market demand for refined oil products (for ease of calculation, the forecast error of the test set is used)
$p$	Prediction value of the average price of refined oil products in the ith period
${\epsilon }_1$	Prediction error of the average price of refined oil products (for ease of calculation, the prediction error of the test set is used)
$Q_s$	Production quantity of refined oil product to meet the needs of the market demand and inventory replenishment demand in the ith period
$t_s$	Replenishment time point of oil depot of the refined oil enterprise
$m_s$	Sales incentive amount
$c_1$	The unit production cost of refined oil products
$c_2$	The storage cost per unit of refined oil products per unit of time
$q$	The amount of residual oil in the oil depot at the start of the ith period (sales surplus of the (i − 1)th period).
$T$	The total time duration of the ith period
${\pi }_s$	The expected profit generated by the production, marketing, and inventory activities of the enterprise in the T period

.

3.2. Model Construction

Since there is a chronological order in the production, sales, and inventory decisions of the refined oil enterprise, the inverse inference method in dynamic programming is used to analyze the replenishment decision in Stage 3. Given the sales incentive amount $m_s$ and production quantity $Q_s$, the refined oil enterprise needs to decide on an optimal time point $t_s$ for inventory replenishment to maximize their expected profits ${\pi }_s$, that is,

$$\begin{gathered} \underset{t_s}{max}{\pi }_s=\left\{\left(p+{\epsilon }_1\right)\cdot \left[q+\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),Q_s\right)\right]-c_1{Q}_s-m_s\right. \\ -\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2-\frac{1}{2}\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),Q_s\right)\mathit{min}\left(T-t_s,\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\right)\cdot c_2 \end{gathered}$$

(1)

$$s.t. \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\le t_s\le T$$

(2)

where $\left(p+{\epsilon }_1\right)\cdot \left[q+\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),Q_s\right)\right]$ is the sales revenue, $c_1{Q}_s$ is the production cost, $m_s$ is the sales incentive amount paid by the refined oil enterprise, $\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2$ is the storage cost of residual oil in the oil depot at the starting time point generated in the subsequent time periods, and $\frac{1}{2}\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),Q_s\right)\mathit{min}\left(T-t_s,\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\right)\cdot c_2$ is the inventory cost incurred by the replenished oil of the oil depot after replenishment time $t_s$. It is worth noting that it is impossible for a refined oil enterprise to replenish the refined oil stock before the residual oil inventory $q$ is used up, due to the fact that such an action will not bring any benefits to the refined oil enterprise but will increase the inventory cost. Therefore, the time point of replenishment must be satisfied with $\frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\le t_s\le T$. That is, the replenishment time is defined to be the time point after the residual oil stock is used up.

Next, the production decision of the refined oil enterprise in Stage 2 is analyzed. Given the sales incentive amount $m_s$, the refined oil enterprise needs to decide on an optimal production quantity $Q_s$ to maximize its expected profits ${\pi }_s$, that is,

$$\begin{gathered} \underset{Q_s}{max}{\pi }_s=\left\{\left(p+{\epsilon }_1\right)\cdot \left[q+\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s^{*}\left(Q_s\right)\right),Q_s\right)\right]-c_1{Q}_s-m_s\right.-\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}} \\ \cdot c_2\left.-\frac{1}{2}\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s^{*}\left(Q_s\right)\right),Q_s\right)\mathit{min}\left(T-t_s^{*}\left(Q_s\right),\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\right)\cdot c_2\right\} \end{gathered}$$

(3)

$$s.t.Q_s\ge 0$$

(4)

where $t_s^{*}\left(Q_s\right)$ is the optimal decision at Stage 3 and is a function of production quantity $Q_s$. The objective function in Equation (3) is almost identical to Equation (1), the unique difference being that $t_s$ is changed to $t_s^{*}\left(Q_s\right)$.

Finally, the sales incentive decision of the refined oil enterprise in Stage 1 is analyzed. Here the enterprise needs to decide on an optimal sales incentive amount $m_s$ to maximize its expected profit ${\pi }_s$, that is,

$$\begin{gathered} \underset{m_s}{max}{\pi }_s=\left\{\left(p+{\epsilon }_1\right)\cdot \left[q+\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s^{*}\left(Q_s^{*}\left(m_s\right)\right)\right),Q_s\right)\right]-c_1{Q}_s^{*}\left(m_s\right)-m_s\right. \\ \left.\begin{array}{c}-\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2-\frac{1}{2}\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s^{*}\left(Q_s^{*}\left(m_s\right)\right)\right),Q_s^{*}\left(m_s\right)\right)\\ \cdot \mathit{min}\left(T-t_s^{*}\left(Q_s^{*}\left(m_s\right)\right),\frac{Q_s^{*}\left(m_s\right)T}{D+{\epsilon }_2+2\sqrt{m_s}}\right)\cdot c_2\end{array}\right\} \end{gathered}$$

(5)

$$s.t. m_s\ge 0$$

(6)

where $Q_s^{*}\left(m_s\right)$ is the optimal decision at Stage 2 and is a function of $m_s$. Similarly, the objective function in Equation (5) is almost identical to Equation (3), the unique difference being that $Q_s$ is changed to $Q_s^{*}\left(m_s\right)$.

4. Solution and Analysis of Production-Sales-Stock Sequential Optimization

4.1. Solution to Production-Sales-Stock Sequential Optimization

By solving the mathematical programming of Equation (1), Lemma 1 can be obtained.

Lemma 1.

Given the sales incentive amount $m_s$and production quantity $Q_s$, the optimal decision on replenishment time point $t_s^{*}$can be represented by

$$t_s^{*}=\left\{\begin{array}{c}T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}},Q_s<\frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\hfill \\ \frac{T{c}_2-p-{\epsilon }_1}{c_2},Q_s\ge \frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\hfill \end{array}\right..$$

Proof. 

Since

$$\mathit{min}\left(\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),Q_s\right)=\left\{\begin{array}{c}\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right),t_s\ge T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\\ Q_s,t_s<T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\end{array}\right.$$

and

$$\mathit{min}\left(T-t_s,\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\right)=\left\{\begin{array}{c}T-t_s,t_s\ge T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\\ \frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}},t_s<T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\end{array}\right.$$

the objective function of Equation (1) can be reduced to the following form.

$${\pi }_s=\{\begin{array}{c}\left(p+{\epsilon }_1\right)\cdot \left(q+Q_s\right)-c_1{Q}_s-m_s-\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2\\ -\frac{1}{2}{Q}_s\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}{c}_2,t_s<T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\\ \left(p+{\epsilon }_1\right)\cdot \left[q+\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right)\right]-c_1{Q}_s-m_s-\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2\\ -\frac{1}{2}\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}\cdot \left(T-t_s\right)\left(T-t_s\right)c_2,t_s\ge T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\end{array}$$

(7)

It is easy to see that Equation (7) is continuous and that the first part of Equation (7) is a constant and the second part is a concave function of $t_s$. The second part of Equation (7) is derived and the first derivative equals zero; then, the solution to the first-order condition is

$$t_s=\frac{T{c}_2-p-{\epsilon }_1}{c_2}.$$

Since it is difficult to determine the size relationship between the above first-order conditional solution and $T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}$, it can be discussed in different cases.

(1) If $\frac{T{c}_2-p-{\epsilon }_1}{c_2}\ge T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}$, that is, $Q_s\ge \frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}$, then the first part of Equation (7) is a constant and the second part is a unimodal function (first increasing and then decreasing), so the maximum value is obtained at the first-order conditional solution. Other than that, since

$$\frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\le \frac{T{c}_2-p-{\epsilon }_1}{c_2}\le T,$$

the first-order conditional solution satisfies the constraint condition (2), so the optimal solution can be expressed by

$$t_s^{*}=\frac{T{c}_2-p-{\epsilon }_1}{c_2}$$

(2) If $\frac{T{c}_2-p-{\epsilon }_1}{c_2}<T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}$, that is, $Q_s<\frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}$, the first part of Equation (7) is constant and the second part is monotonically decreasing, so the maximum value is obtained at the dividing point. Similarly, since

$$\frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\le T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}\le T,$$

the demarcation point satisfies the constraint (2), so the optimal solution is

$$t_s^{*}=T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}$$

In summary, the optimal solution can be represented in the following form.

$$t_s^{*}=\left\{\begin{array}{c}T-\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}},Q_s<\frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\\ \frac{T{c}_2-p-{\epsilon }_1}{c_2},Q_s\ge \frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\end{array}\right.$$

(8)

□

Lemma 2.

Given the sales incentive amount$m_s$, the optimal production decision of the refined oil enterprise can be given by

$$Q_s^{*}=\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}.$$

Proof. 

Substituting Equation (8) into Equation (3), one obtains

$${\pi }_s=\{\begin{array}{c}\left(p+{\epsilon }_1\right)\cdot \left(q+Q_s\right)-c_1{Q}_s-m_s-\frac{q}{2}\cdot \frac{qT}{D+{\epsilon }_2+2\sqrt{m_s}}\cdot c_2\\ -\frac{1}{2}{Q}_s\frac{Q_{s}T}{D+{\epsilon }_2+2\sqrt{m_s}}{c}_2,Q_s<\frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\\ \frac{\left(p+{\epsilon }_1\right)\left(2\sqrt{m_s}p+2\sqrt{m_s}{\epsilon }_1+2qT{c}_2+Dp+D{\epsilon }_1+p{\epsilon }_1+{\epsilon }_1{\epsilon }_2\right)}{2T{c}_2}\\ -c_1{Q}_s-m_s-\frac{q^{2}T{c}_2}{2\left(D+{\epsilon }_2+2\sqrt{m_s}\right)},Q_s\ge \frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}\end{array}$$

(9)

It is easy to see that Equation (9) is continuous, and that the first part of Equation (9) is the concave function of $Q_s$ and the second part is the monotonic decreasing function about $Q_s$. The first part of Equation (9) is derived and the first derivative equals zero; then, the first-order condition is solved by

$$Q_s=\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}.$$

Since $\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}-\frac{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)\left(p+{\epsilon }_1\right)}{T{c}_2}=-\frac{c_1\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}<0$ and the above first-order conditional solution satisfies the constraint condition (4), the first-order conditional solution is the optimal solution, i.e.,

$$Q_s^{*}=\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}$$

(10)

□

Lemma 3.

The optimal sales incentive amount $m_s^{*}$is the unique root of the Equation $f\left(m_s^{*}\right)=0$, wherein

$$f\left(m_s^{*}\right)=2\frac{{(p+{\epsilon }_1-c_1)}^2}{T{c}_2\sqrt{m_s^{*}}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s^{*}}\right)}^2\sqrt{m_s^{*}}}-1.$$

Proof. 

Substituting Equation (10) into Equation (8), one obtains

$$t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2}$$

(11)

Substituting Equations (10) and (11) into Equation (5), we obtain

$$\begin{gathered} {\pi }_s=\left(p+{\epsilon }_1\right)\left[\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2}+q\right]-\frac{c_1\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{T{c}_2} \\ -m_s-\frac{T{c}_2}{2\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}\left[\frac{{(p+{\epsilon }_1-c_1)}^2{(D+{\epsilon }_2+2\sqrt{m_s})}^2}{T^2{c}_2{}^2}+q^2\right] \end{gathered}$$

(12)

Equation (12) can be further simplified into the following form, i.e.,

$${\pi }_s=\frac{{(p+{\epsilon }_1-c_1)}^2\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}{2T{c}_2}-\frac{T{c}_2{q}^2}{2\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}+\left(p+{\epsilon }_1\right)q-m_s$$

(13)

To find a first derivative of Equation (13), we can obtain

$$\frac{\partial {\pi }_s}{\partial m_s}=\frac{{\left(x-c_1\right)}^2}{2T{c}_2\sqrt{m_s}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}^2\sqrt{m_s}}-1$$

(14)

Since $\frac{{\partial }^2{\pi }_s}{\partial m_s{}^2}=-\frac{4q^2{T}^2{c}_2{}^2{m}_s{}^{\frac{3}{2}}+q^2{T}^2{c}_2{}^2\left(D+{\epsilon }_2+2\sqrt{m_s}\right)m_s+{(p+{\epsilon }_1-c_1)}^2{(D+{\epsilon }_2+2\sqrt{m_s})}^3{m}_s}{4m_s{}^{\frac{5}{2}}{T}^2{c}_2{}^2{(D+{\epsilon }_2+2\sqrt{m_s})}^3}<0$, Equation (13) is the concave function about $m_s$ and has a unique maximum value point. Moreover, Equation (14) is the monotonical decreasing function about $m_s$.

Since

$$\underset{m_s\to 0}{lim}\frac{{\left(x-c_1\right)}^2}{2T{c}_2\sqrt{m_s}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}^2\sqrt{m_s}}-1=\infty$$

and

$$\underset{m_s\to \infty }{lim}\frac{{\left(x-c_1\right)}^2}{2T{c}_2\sqrt{m_s}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}^2\sqrt{m_s}}-1=-1$$

the following equation holds:

$$\frac{{\left(x-c_1\right)}^2}{2T{c}_2\sqrt{m_s}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s}\right)}^2\sqrt{m_s}}-1=0.$$

This equation only has one unique root and that root is the optimal solution. □

4.2. Decision Analysis of Production-Sales-Stock Sequential Optimization

Combining Lemmas 1–3, Proposition 1 can be found.

Proposition 1.

Under sequential decision-making, the optimal sales incentive amount $m_s^{*}$in the ith ($i\in \left\{1,2,\dots ,n\right\}$) period is satisfied

$$\frac{2{(p+{\epsilon }_1-c_1)}^2}{T{c}_2\sqrt{m_s^{*}}}+\frac{T{c}_2{q}^2}{2{\left(D+{\epsilon }_2+2\sqrt{m_s^{*}}\right)}^2\sqrt{m_s^{*}}}-1=0$$

(15)

and $m_s^{*}$is the only root of the above equation. Therefore, the optimal production decision of the refined oil enterprise is expressed by

$$Q_s^{*}=\frac{\left(p+{\epsilon }_1-c_1\right)\left(D+{\epsilon }_2+2\sqrt{m_s^{*}}\right)}{T{c}_2}$$

(16)

The optimal time point for inventory replenishment is given by

$$t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2}$$

(17)

The optimal expected profit of the refined oil enterprise can be represented by

$${\pi }_s^{*}=\frac{{(p+{\epsilon }_1-c_1)}^2\left(D+{\epsilon }_2+2\sqrt{m_s^{*}}\right)}{2T{c}_2}-\frac{T{c}_2{q}^2}{2\left(D+{\epsilon }_2+2\sqrt{m_s^{*}}\right)}+\left(p+{\epsilon }_1\right)q-m_s^{*}$$

(18)

Proof. 

Combining Lemmas 1–3, it is easy to obtain Proposition 1. □

Proposition 1 shows that the optimal production quantity of a refined oil enterprise in any period (i.e., Period i) is determined by the price of refined oil products $p+{\epsilon }_1$, the unit production cost $c_1$, the market demand per unit time $\frac{D+{\epsilon }_2+2\sqrt{m_s}}{T}$, and the inventory cost per unit of product per unit time $c_2$. Proposition 1 also states that the optimal replenishment time point for an oil depot in any period (i.e., Period i) is determined by the total duration ($T$) of that period, the price of refined oil products $p+{\epsilon }_1$, the production cost per unit $c_1$, and the inventory cost per unit of product per unit of time $c_2$, but is not related to sales incentives. This is because refined oil enterprises mainly respond to market demand through production and control inventory with replenishment time points, so the impact of sales incentives on market demand is only reflected in production, but has no impact on the timing of replenishment.

Proposition 1 has important practical significance. Since Proposition 1 gives the optimal production and inventory decisions in any period, the results can be used in each period of decision-making. This means that a decision support system can be established based on Proposition 1 and optimal decision-making and optimal inventory control in each period of production can be achieved to maximize the long-term profits of refined oil enterprises.

Proposition 2.

If the prediction is completely accurate then, at the end of the ith period, the refined oil enterprise either runs out of inventory or is out of stock, i.e.,$\frac{Q_s^{*}T}{D+{\epsilon }_2+2\sqrt{m_s^{*}}}\le T-t_s^{*}$.

Proof. 

In terms of Lemmas 1–3, Proposition 2 is clearly true. □

Proposition 2 means that if the prediction is 100% accurate, refined oil enterprises would rather be out of stock than leave inventory in the next period. Because the inventory is left over in the next period, it is impossible to generate revenue in the current period, but the inventory cost rises. However, this does not mean that refined oil enterprises will never leave inventory for the next period due to the fact that forecasts cannot be 100% accurate. Therefore, when building the sequential optimal decision model, this paper considers the generalized situation. That is, at the beginning of each period, it is assumed that there is residual oil q in the oil depot.

Proposition 3.

Optimal inventory replenishment time points are monotonically increasing (i.e., $\frac{\partial t_s^{*}}{\partial c_1}>0$, $\frac{\partial t_s^{*}}{\partial c_2}>0$, $\frac{\partial t_s^{*}}{\partial T}>0$) with respect to production costs, inventory costs, and the total duration of the ith period. However, they have nothing to do with sales incentives (i.e., $\frac{\partial t_s^{*}}{\partial m_s^{*}}=0$).

Proof. 

Since $t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2}$, we can obtain

$$\frac{\partial t_s^{*}}{\partial c_1}>0,\frac{\partial t_s^{*}}{\partial c_2}>0,\frac{\partial t_s^{*}}{\partial T}>0,\frac{\partial t_s^{*}}{\partial m_s^{*}}=0.$$

□

Proposition 3 implies that with the increase of production costs, inventory costs, and the total duration of the ith period, refined oil enterprises will postpone the timing of ordering, i.e., they will lengthen the out-of-stock period after the residual inventory is used up and before the replenishment time comes, but this out-of-stock period has nothing to do with sales incentives. This is because the optimal replenishment time point is used to adjust the total inventory cost and focuses primarily on the unit profit rate and the total duration of the ith period, regardless of sales incentives. The response to sales incentives is mainly reflected in production quantity.

Subsequently, the impact of refined oil price forecasts and demand forecasts on production-sales-stock sequential optimization decision-making is analyzed separately, as detailed in Section 5.

5. Impact Analysis of Predictions on Sequential Optimization Decision-Making

5.1. Effect of Price Forecasting on Sequential Optimization Decision-Making

In this subsection, the impact of the predicted value and forecast error of the refined oil price on the decision of the inventory replenishment time point is analyzed. We can obtain Corollary 1 and Corollary 2.

Corollary 1.

The optimal inventory replenishment time point decreases monotonically with the predicted value of the refined oil price (i.e.,$\frac{\partial t_s^{*}}{\partial p}<0$).

Proof. 

Since $t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2}$, we have $\frac{\partial t_s^{*}}{\partial p}<0$. □

Corollary 1 means that as the price forecast increases, the refined oil enterprise will advance the ordering time point. That is, the out-of-stock period is shortened or even disappeared after the residual inventory is used up and before the replenishment time period comes. This is because the main role of the optimal replenishment time point is to adjust the inventory. Thus, the higher the price, the less concerned the enterprise is about the inventory cost, so the stock-out period will become shorter or even disappear.

Corollary 2.

If the prediction error of the refined oil price is positive (i.e., ${\epsilon }_1>0$), the optimal inventory replenishment time point decreases monotonically with that error (i.e., $\frac{\partial t_s^{*}}{\partial {\epsilon }_1}<0$, what the negative derivative means is that the inventory replenishment time point decreases monotonically with the prediction error). If the prediction error of the refined oil price is negative (i.e., ${\mathsf{\epsilon }}_1<0$), the optimal inventory replenishment time point increases monotonically with that error (i.e., $\frac{\partial t_s^{*}}{\partial {\epsilon }_1}>0$).

Proof. 

Since $t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2}$, we can obtain $\frac{\partial t_s^{*}}{\partial {\epsilon }_1}<0$ when ${\epsilon }_1>0$. Similarly, when ${\epsilon }_1<0$, we can obtain $\frac{\partial t_s^{*}}{\partial {\epsilon }_1}>0$. □

Corollary 2 means that if the actual value of the refined oil price is higher than the predicted value, the enterprise will advance the ordering time point, and the higher it is, the more obvious the advance effect will be. If the actual value of the refined oil price is lower than the forecasted value, the refined oil enterprise will delay the ordering time point, and the lower it is, the more obvious the delay effect will be. The reasons behind Corollary 2 are similar to those behind Corollary 1 and will not be repeated here.

Next, the numerical analysis method is used to analyze the impact of the predicted value and the forecasted error of the refined oil price on the optimal sales incentive decision, the optimal production decision, and the expected profit; the corresponding results are illustrated in Figure 1. The values of the relevant parameters in the optimal models are shown in

Table 2. The parametric values of the sequential optimization decision model when the predicted values of refined oil price are used.

Symbol	Value	Unit
$D$	100	Ton
${\epsilon }_2$	5	Ton
${\epsilon }_1$	0.5	Thousand yuan/ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter

[26]. It is worth noting that the unit of price is 1000 yuan/ton, the unit of sales incentives is 1000 yuan, the unit of production is ton, and the unit of profit is 1000 yuan in Figure 1.

Figure 1a shows that the sales incentives increases with the increase of price prediction value, and this effect increases marginally. This is because, as the price increases, the use of sales incentives to increase the sales amount of refined oil products can bring more profits, so the sales incentives of refined oil enterprises increase monotonically with the price prediction value. Moreover, in the case of constant production costs, the increase in price will lead to an increase in the unit profit margin, so the profit increase effect due to sales incentives will be more obvious (that is, marginal increase). Figure 1b shows that the production quantity of refined oil enterprises increases monotonically with the predicted value of the refined oil price. This is because the optimal production decision is essentially to find a balance between sales revenue and inventory cost, and the expected price increase will increase sales revenue, so the above balance will move upwards. Figure 1c shows that the expected profit of the refined oil enterprise increases with the increase in the price forecasted value and the increasing effect is marginal. This is because, as the sales price of refined oil products increases, the total profit of the enterprise will obviously increase. Moreover, in the case of constant production costs, an increase in prices will lead to an increase in the unit profit rate, so the increasing effect of the total profit will be more obvious (i.e., a marginal increase).

Similarly, the numerical analysis method is used to analyze the impact of price prediction error on the optimal sales incentive decision, the optimal production decision, and the expected profit; the corresponding results are reported in Figure 2. Accordingly, the values of the relevant parameters of sequential optimal decision models are shown in

Table 3. The parametric values of the sequential optimization decision model when the prediction error of refined oil price is used.

Symbol	Value	Unit
$D$	100	Ton
${\epsilon }_2$	5	Ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter
p	8	Thousand yuan/ton

. It is worth noting that the unit of price prediction error is 1000 yuan/ton, the unit of sales incentives is 1000 yuan, the unit of production is ton, and the unit of profit is 1000 yuan in Figure 2.

Figure 2 shows that the sales incentives and expected profits of refined oil enterprises increase with the increase of the relative error of price forecasting, and the effect of this increase is marginal. Moreover, the production quantity of refined oil enterprises also increases monotonically with the relative error of price forecasting. This is because the above error is the relative error of the testing set; the greater the relative error, the higher the expected price. Thus, the impact of relative errors of refined oil price forecasting on sales incentives, production volumes, and expected profits is similar to the impact of price prediction values.

5.2. Effect of Demand Forecasting on Sequential Optimization Decision-Making

In this subsection, the impact of the prediction value and the relative error of the market demand on the timing decision of inventory replenishment is analyzed. We can obtain Corollary 3.

Corollary 3.

The optimal inventory replenishment time point is independent of the prediction value and the prediction error of market demand (i.e.,$\frac{\partial t_s^{*}}{\partial D}=0$ and $\frac{\partial t_s^{*}}{\partial {\epsilon }_2}=0$).

Proof. 

Since

$$t_s^{*}=T-\frac{p+{\epsilon }_1-c_1}{c_2},$$

we can obtain $\frac{\partial t_s^{*}}{\partial D}=0$ and $\frac{\partial t_s^{*}}{\partial {\epsilon }_2}=0$. □

The reason behind Corollary 3 is that the optimal replenishment time point is used to adjust the total inventory cost, so the decision on it is mainly focused on the unit profit margin and the total duration of the ith period, regardless of the demand forecast value and its forecast error. The response to demand is mainly reflected in production.

Based on the above theoretical analysis, the impact of demand forecast values on optimal sales incentive decisions, production decisions, and expected profits is then analyzed; the corresponding results are illustrated in Figure 3. Accordingly, the values of the relevant parameters of sequential optimal decision models are shown in

Table 4. The parametric values of the sequential optimization decision model when the prediction values of refined oil demand are used.

Symbol	Value	Unit
${\epsilon }_2$	5	Ton
${\epsilon }_1$	0.5	Thousand yuan/ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter
p	8	Thousand yuan/ton

. Note that the unit of sales incentives is 1000 yuan, the unit of demand and production is ton, and the unit of profit is 1000 yuan in Figure 3.

Figure 3a shows that the sales incentives of the refined oil enterprise weaken as the demand forecast increases, and this attenuation effect is increases marginally. This is because, with the increase of demand, refined oil enterprises are less willing to use sales incentives to increase sales of refined oil products. Moreover, in the case of high demand, if the sales incentives are added, it will increase the cost of inventory sharply, so this weakening effect is marginally incremental. Figure 3b shows that the production quantity of refined oil enterprises increases monotonically with the forecast value of market demand. This is due to the fact that optimal production quantity is a response to demand, so the higher the demand, the higher the production. Figure 3c shows that the expected profit of the refined oil enterprise increases with the increase of the demand forecast value. This is because the increase in demand leads to an increase in sales, and the total profit will naturally increase.

Likewise, we analyze the impact of demand forecast error on optimal sales incentive decisions, production decisions, and expected profits; the corresponding results are shown in Figure 4. Accordingly, the values of the relevant parameters of sequential optimal decision models are shown in

Table 5. The parametric values of the sequential optimization decision model when the prediction errors of refined oil demand are used.

Symbol	Value	Unit
$D$	100	Ton
${\epsilon }_1$	0.5	Thousand yuan/ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter
p	8	Thousand yuan/ton

. It is worth noting that the unit of sales incentives is 1000 yuan, the unit of demand prediction error and production is ton, and the unit of profit is 1000 yuan in Figure 4.

Figure 4 shows that the sales incentives of refined oil enterprises weaken with the increase of the relative error of demand forecasting, and this weakening effect is increases marginally, while the production quantity and expected profit of refined oil enterprises increase monotonically with the relative error of demand forecasting. This is because the above relative error is the relative error on the test set. That is, the greater the relative error, the higher the expected price. Therefore, the impact of demand forecasting relative errors on sales incentives, production quantity, and expected profits is similar to the impact of demand predictions.

5.3. Joint Effect of Price and Demand Forecasting on Sequential Optimization Decision-Making

In this subsection, the joint effects of price and demand forecasts on optimal sales incentive decisions, optimal production quantity decisions, and expected profits are analyzed, as elaborated in Figure 5. Accordingly, the values of the relevant parameters of sequential optimal decision models are shown in

Table 6. The parametric values of the sequential optimization decision model when the prediction values of refined oil price and demand are used.

Symbol	Value	Unit
${\epsilon }_2$	5	Ton
${\epsilon }_1$	0.5	Thousand yuan/ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter

. It is worth noting that the unit of price is 1000 yuan/ton, the unit of sales incentives is 1000 yuan, the unit of demand and production is ton, and the unit of profit is 1000 yuan in Figure 5.

Figure 5a shows that, although sales incentives strengthen with increasing prices and weaken with increasing demand, when prices and demand increase at the same time, the strengthening effect of the above sales incentives will mask their weakening effects, resulting in an overall upward trend in sales incentives. This is because refined oil enterprises reduce sales incentives to control inventory costs as demand increases. However, when the prices also increase, refined oil enterprises are less concerned about inventory costs and more about sales revenue. Therefore, when prices and demand increase at the same time, sales incentives generally show an upward trend. Figure 5b shows that the production quantity of refined oil enterprises increases with the increase of prices and demand, and the growth in the direction of demand is slower and the growth in the direction of price is faster. This is because, in the case of increased demand at constant prices, the increase in production will lead to excessively high inventory costs, so refined oil enterprises tend to be conservative in increasing production. In the case of constant demand and increased prices, refined oil enterprises are less concerned about inventory costs, so refined oil enterprises tend to be aggressive in production increases. Figure 5c shows that the profit of refined oil enterprises increases with the increase of prices and demand, and the growth in the direction of demand is slower and the growth in the direction of price is faster. This is because, in the case of increased demand at constant prices, although enterprises can increase sales, this also increases the inventory cost. That is, the growth rate of net profit per unit is small, and in the case of demand increase and constant price, the unit net profit of enterprises can achieve a large increase. Therefore, the profits of enterprises grow slower in the direction of demand and grow faster in the direction of prices.

Finally, the joint effect of price and demand forecast error on the optimal sales incentive decision, production quantity decision, and expected profit are analyzed by numerical analysis method; the corresponding results are reported in Figure 6. For the numerical analysis, the values of the relevant parameters of sequential optimal decision models are shown in

Table 7. The parametric values of the sequential optimization decision model when the prediction errors of refined oil price and demand are used.

Symbol	Value	Unit
$D$	100	Ton
$c_1$	4	Thousand yuan/ton
$c_2$	2	Thousand yuan/ton/quarter
$q$	5	Ton
$T$	1	Quarter
p	8	Thousand yuan/ton

. It is worth noting that the unit of price forecast error is 1000 yuan/ton, the unit of sales incentives is 1000 yuan, the unit of demand prediction error and production is ton, and the unit of profit is 1000 yuan in Figure 6.

Figure 6a shows that, although sales incentives are strengthened with the increase of the relative error of price forecasting and weakened with the increase of the relative error of demand forecasting, the strengthening effect of the above sales incentives will mask the weakening effect when the relative errors of price and demand forecasting increase simultaneously. As a result, sales incentives generally show a rising tendency. Figure 6b shows that the production quantity of refined oil enterprises increases with the increase of relative errors in price and demand forecasts, and growth in the direction of demand is slower, while it is faster in the direction of price. Figure 6c shows that expected profits increase with the increase in the relative error of price and demand forecasts, and growth is slower in the direction of demand and faster in the direction of price. The reason behind these conclusions is that the greater the relative error in price and demand forecasting, the higher the price and demand.

5.4. Summary

According to the above theoretical and numerical analyses, four main findings can be summarized below.

(1) In optimal decision-making for any period, refined oil enterprises would rather be out of stock than leave the inventory in the next period if prediction is 100% accurate. Because the inventory is left over to the next period, it is impossible to generate any revenue from it in the current period, but it raises the cost of inventory. However, this does not mean that refined oil enterprises will never leave inventory for the next period because predictions cannot be 100% accurate. In addition, the optimal inventory replenishment time point is increases monotonically regarding production costs, inventory costs, and the total duration of any period, but is independent of sales incentives. This is because the primary role of the optimal replenishment point is to adjust the total inventory cost, so decision on it are mainly focused on the unit profit margin and the total duration of the ith, regardless of sales incentives. The response to sales incentives is mainly reflected in production quantity.

(2) On the impact of price forecasts on sequential optimal decision-making, refined oil enterprises will advance the ordering time point with the increase of the forecast value of the refined oil price. That is, the out-of-stock period will be shortened or even disappear after the residual inventory is used up and before the replenishment comes. If the actual value of the refined oil price is higher than the predicted value, the enterprise will advance the ordering time point, and the higher it is, the more obvious the advance effect. Similarly, if the actual value of the price is lower than the predicted value, the refined oil enterprises will delay the ordering time point; the lower it is, the more obvious the delay effect. The sales incentives and expected profits of refined oil enterprises increase with the increase of the price forecast value, and this increasing effect is marginal. The production quantity of enterprises also increases monotonically with the increase of the forecast value and the relative forecast error of the refined oil price. The sales incentives and expected profits increase with the increase of the relative error of price prediction, and this increasing effect is marginal.

(3) On the impact of demand forecasting on sequential optimal decision-making, the optimal inventory replenishment time point of refined oil enterprises is independent of the forecast value and forecast error of market demand. The sales incentives of the enterprise weaken with the increase of demand forecast value and relative forecast error, and this weakening effect is marginal. The production quantity and expected profits increase monotonically with the forecast value of demand. Moreover, the production quantity and expected profit also increase monotonically with the relative error of demand forecasting.

(4) On the joint effect of price and demand forecasting on sequential optimal decision-making, sales incentives strengthen with increasing prices and weaken with increasing demand, but when the price and demand increase at the same time, the enhanced effect of the above sales incentives will mask their weakening effects, leading to an overall upward trend in sales incentives. The production quantity of refined oil enterprises increases with the increase of price and demand; the growth in the direction of demand is relatively conservative and the growth in the direction of prices is more aggressive. The profits of enterprises also increase with the increase of price and demand; the growth in the direction of demand is slower and the growth in the direction of price is faster. In addition, this paper also finds that, although sales incentives strengthen with the increase of the relative error of price forecasting and weaken with the increase of the relative error of demand forecasting, when the relative errors of price and demand forecasts increase at the same time, the strengthening effect of the above sales incentives will mask the weakening effect, resulting in an overall upward trend in sales incentives.

6. Conclusions

In this paper, a prediction-driven sequential optimization method for production-sales-stock decision-making problems in refined oil enterprises is investigated in detail. For the sequential optimization decision-making problems, three dynamic nonlinear programming models are first constructed. Then, the analytical solutions to sequential optimization for production-sales-stock decision-making issues are presented. Finally, the effect of price forecasting and demand forecasting on sequential optimization for production-sales-stock decision-making are analyzed thoroughly. Numerical analysis results demonstrated the significant effect of forecasting results of refined oil price and market demand on production-sales-stock decision-making, indicating that the prediction-driven sequential optimization methodology can be used as a feasible solution to joint optimization for production-sales-stock decision-making.

However, this paper only reports the impact results of prediction results on sequential optimization for production-sales-stock decision-making; the effects of prediction results on simultaneous optimization of production-sales-stock decision-making are not analyzed. As one of the joint optimization methods, the results of simultaneous optimization are very important for decision-makers in the joint decision-making of production-sales-stock task. We will look into this issue in the near future.