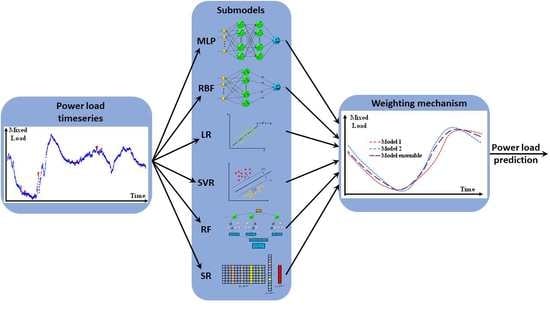
A Machine Learning Model Ensemble for Mixed Power Load Forecasting across Multiple Time Horizons
Abstract
:1. Introduction
2. Materials and Methods
2.1. Machine-Learning Methods Short Description
2.1.1. Linear Regression
2.1.2. Sparse Coding
2.1.3. Support Vector Regression
2.1.4. Neural Networks
2.1.5. Random Forests
2.2. Machine-Learning Model Ensemble
3. Case Study
3.1. Problem and Data Description
3.2. Data Preprocessing and Model Training
4. Results
5. Discussion
6. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AP | active power |
| LR | linear regression |
| ML | Machine-learning |
| MAE | mean absolute error |
| MLP | multi-layer perceptron |
| NN | neural network |
| RBF | radial basis function |
| RF | random forests |
| RES | renewable energy sources |
| SBL | sparse Bayesian learning |
| SR | sparse regression |
| SVR | support vector regression |
References
- Livanos, N.-A.I.; Hammal, S.; Giamarelos, N.; Alifragkis, V.; Psomopoulos, C.S.; Zois, E.N. OpenEdgePMU: An Open PMU Architecture with Edge Processing for Future Resilient Smart Grids. Energies 2023, 16, 2756. [Google Scholar] [CrossRef]
- Chen, H.; Xuan, P.; Wang, Y.; Tan, K.; Jin, X. Key Technologies for Integration of Multitype Renewable Energy Sources—Research on Multi-Timeframe Robust Scheduling/Dispatch. IEEE Trans. Smart Grid 2016, 7, 471–480. [Google Scholar] [CrossRef]
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.N.; Livanos, N.A.; Alexandridis, A. Metaheuristic Search in Smart Grid: A Review with Emphasis on Planning, Scheduling and Power Flow Optimization Applications. Renew. Sustain. Energy Rev. 2021, 145, 111072. [Google Scholar] [CrossRef]
- Salkuti, S.R. Day-Ahead Thermal and Renewable Power Generation Scheduling Considering Uncertainty. Renew. Energy 2019, 131, 956–965. [Google Scholar] [CrossRef]
- Gong, L.; Wang, X.; Tian, M.; Yao, H.; Long, J. Multi-Objective Optimal Planning for Distribution Network Considering the Uncertainty of PV Power and Line-Switch State. Sensors 2022, 22, 4927. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Rakopoulos, D.; Blanas, O.; Psomopoulos, S.; Munteanu, R.A.; Agavanakis, K. Day Ahead Optimal Dispatch Schedule in a Smart Grid Containing Distributed Energy Resources and Electric Vehicles. Sensors 2021, 21, 7295. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Xia, Q.; Ding, Y.; Huang, Y.; Sun, R.; Huang, J.; Bai, J. A Convex Model of Risk-Based Unit Commitment for Day-Ahead Market Clearing Considering Wind Power Uncertainty. IEEE Trans. Power Syst. 2015, 30, 1582–1592. [Google Scholar] [CrossRef]
- Divenyi, D.; Polgari, B.; Raisz, D.; Sleisz, A.; Sores, P. Special Session on Proposal of a New European Co-Optimized Energy and Ancillary Service Market Design—Part II. In Proceedings of the International Conference on the European Energy Market, EEM, Porto, Portugal, 6–9 June 2016; Volume 2016. [Google Scholar]
- Tayab, U.B.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-Term Load Forecasting for Microgrid Energy Management System Using Hybrid HHO-FNN Model with Best-Basis Stationary Wavelet Packet Transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Zedan, H.A.; ElDesouky, A.A. Energy Management of Microgrids Using Load Shifting and Multi-Agent System. J. Control Autom. Electr. Syst. 2020, 31, 1015–1036. [Google Scholar]
- Basir, R.; Qaisar, S.; Ali, M.; Aldwairi, M.; Ashraf, M.I.; Mahmood, A.; Gidlund, M. Fog Computing Enabling Industrial Internet of Things: State-of-the-Art and Research Challenges. Sensors 2019, 19, 4807. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Han, H. A Lightweight and Privacy-Friendly Data Aggregation Scheme against Abnormal Data. Sensors 2022, 22, 1452. [Google Scholar] [CrossRef]
- Papadimitrakis, M.; Kapnopoulos, A.; Tsavartzidis, S.; Alexandridis, A. A Cooperative PSO Algorithm for Volt-VAR Optimization in Smart Distribution Grids. Electr. Power Syst. Res. 2022, 212, 108618. [Google Scholar] [CrossRef]
- Haupt, S.E.; Dettling, S.; Williams, J.K.; Pearson, J.; Jensen, T.; Brummet, T.; Kosovic, B.; Wiener, G.; McCandless, T.; Burghardt, C. Blending Distributed Photovoltaic and Demand Load Forecasts. Sol. Energy 2017, 157, 542–551. [Google Scholar] [CrossRef]
- Pan, Y.; Zheng, J.; Yang, Y.; Zhu, R.; Zhou, C.; Shi, T. An Electricity Load Forecasting Approach Combining DBN-Based Deep Neural Network and NAR Model for the Integrated Energy Systems. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing, BigComp, Kyoto, Japan, 27 February–2 March 2019. [Google Scholar]
- Kaur, A.; Nonnenmacher, L.; Coimbra, C.F.M. Net Load Forecasting for High Renewable Energy Penetration Grids. Energy 2016, 114, 1073–1084. [Google Scholar] [CrossRef]
- Van der Meer, D.W.; Munkhammar, J.; Widén, J. Probabilistic Forecasting of Solar Power, Electricity Consumption and Net Load: Investigating the Effect of Seasons, Aggregation and Penetration on Prediction Intervals. Sol. Energy 2018, 171, 397–413. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, Y.; Fan, S.; Hu, X.; Huang, Y.; Lu, Z.; Liu, Y. Multi-Task Short-Term Reactive and Active Load Forecasting Method Based on Attention-LSTM Model. Int. J. Electr. Power Energy Syst. 2022, 135, 107517. [Google Scholar] [CrossRef]
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective; Academic Press: Cambridge, MA, USA, 2015; ISBN 9780128017227. [Google Scholar]
- Wang, C.; Grozev, G.; Seo, S. Decomposition and Statistical Analysis for Regional Electricity Demand Forecasting. Energy 2012, 41, 313–325. [Google Scholar] [CrossRef]
- Gerossier, A.; Girard, R.; Kariniotakis, G.; Michiorri, A. Probabilistic Day-Ahead Forecasting of Household Electricity Demand. CIRED Open Access Proc. J. 2017, 2017, 2500–2504. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, S.; Li, W.; Qu, M. Power Load Probability Density Forecasting Using Gaussian Process Quantile Regression. Appl. Energy 2018, 213, 499–509. [Google Scholar] [CrossRef]
- Vu, D.H.; Muttaqi, K.M.; Agalgaonkar, A.P. Assessing the Influence of Climatic Variables on Electricity Demand. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Xie, J.; Chen, Y.; Hong, T.; Laing, T.D. Relative Humidity for Load Forecasting Models. IEEE Trans. Smart Grid 2018, 9, 191–198. [Google Scholar] [CrossRef]
- Alzate, C.; Sinn, M. Improved Electricity Load Forecasting via Kernel Spectral Clustering of Smart Meters. In Proceedings of the IEEE International Conference on Data Mining, ICDM 2013, Dallas, TX, USA, 7–10 December 2013; pp. 943–948. [Google Scholar]
- Rossi, M.; Brunelli, D. Electricity Demand Forecasting of Single Residential Units. In Proceedings of the 2013 IEEE Workshop on Environmental, Energy and Structural Monitoring Systems, EESMS, Trento, Italy, 11–12 September 2013. [Google Scholar]
- Damrongkulkamjorn, P.; Churueang, P. Monthly Energy Forecasting Using Decomposition Method with Application of Seasonal ARIMA. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005. [Google Scholar] [CrossRef]
- Ould Mohamed Mahmoud, M.; Mhamdi, F.; Jaïdane-Saïdane, M. Long Term Multi-Scale Analysis of the Daily Peak Load Based on the Empirical Mode Decomposition. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009. [Google Scholar] [CrossRef]
- Clements, A.E.; Hurn, A.S.; Li, Z. Forecasting Day-Ahead Electricity Load Using a Multiple Equation Time Series Approach. Eur. J. Oper. Res. 2016, 251, 522–530. [Google Scholar] [CrossRef] [Green Version]
- Elrazaz, Z.S.; Mazi, A.A. Unified Weekly Peak Load Forecasting for Fast Growing Power System. IEE Proc. C Gener. Transm. Distrib. 2010, 136, 29. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-Based Decoupled Time Series Forecasting of Electric Vehicle Charging Demand for Stochastic Power System Operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Yu, C.N.; Mirowski, P.; Ho, T.K. A Sparse Coding Approach to Household Electricity Demand Forecasting in Smart Grids. IEEE Trans. Smart Grid 2017, 8, 738–748. [Google Scholar] [CrossRef]
- Yang, D.; Xu, L.; Gong, S.; Li, H.; Peterson, G.D.; Zhang, Z. Joint Electrical Load Modeling and Forecasting Based on Sparse Bayesian Learning for the Smart Grid. In Proceedings of the 2011 45th Annual Conference on Information Sciences and Systems, CISS 2011, Baltimore, MD, USA, 23–25 March 2011. [Google Scholar]
- Sun, X.; Wang, X.; Wu, J.; Liu, Y. Hierarchical Sparse Learning for Load Forecasting in Cyber-Physical Energy Systems. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Minneapolis, MN, USA, 6–9 May 2013. [Google Scholar]
- Duan, Q.; Sheng, W.X.; Ma, Y.; Ma, K. Sparse Bayesian Learning Using Combined Kernels for Medium Term Load Forecasting. In Proceedings of the 2nd IET Renewable Power Generation Conference (RPG 2013), Beijing, China, 9–11 September 2013. [Google Scholar]
- Giamarelos, N.; Zois, E.N.; Papadimitrakis, M.; Stogiannos, M.; Livanos, N.A.-I.; Alexandridis, A. Short-Term Electric Load Forecasting with Sparse Coding Methods. IEEE Access 2021, 9, 102847–102861. [Google Scholar] [CrossRef]
- Azad, M.K.; Uddin, S.; Takruri, M. Support Vector Regression Based Electricity Peak Load Forecasting. In Proceedings of the 11th International Symposium on Mechatronics and its Applications, ISMA 2018, Sharjah, United Arab Emirates, 4–6 March 2018; pp. 1–5. [Google Scholar]
- Che, J.; Wang, J. Short-Term Load Forecasting Using a Kernel-Based Support Vector Regression Combination Model. Appl. Energy 2014, 132, 602–609. [Google Scholar] [CrossRef]
- Li, Y.; Che, J.; Yang, Y. Subsampled Support Vector Regression Ensemble for Short Term Electric Load Forecasting. Energy 2018, 164, 160–170. [Google Scholar] [CrossRef]
- Ghelardoni, L.; Ghio, A.; Anguita, D. Energy Load Forecasting Using Empirical Mode Decomposition and Support Vector Regression. IEEE Trans. Smart Grid 2013, 4, 549–556. [Google Scholar] [CrossRef]
- Hafeez, G.; Khan, I.; Jan, S.; Shah, I.A.; Khan, F.A.; Derhab, A. A Novel Hybrid Load Forecasting Framework with Intelligent Feature Engineering and Optimization Algorithm in Smart Grid. Appl. Energy 2021, 299, 117178. [Google Scholar] [CrossRef]
- Korovesis, N.; Kandris, D.; Koulouras, G.; Alexandridis, A. Robot Motion Control via an Eeg-Based Brain–Computer Interface by Using Neural Networks and Alpha Brainwaves. Electronics 2019, 8, 1387. [Google Scholar] [CrossRef] [Green Version]
- Akarslan, E.; Hocaoglu, F.O. Electricity Demand Forecasting of a Micro Grid Using ANN. In Proceedings of the 2018 9th International Renewable Energy Congress, IREC, Hammamet, Tunisia, 20–22 March 2018; pp. 1–5. [Google Scholar]
- Pandey, A.K.; Sahay, K.B.; Chandra, D.; Tripathi, M.M. Day Ahead Load Forecast in ISO New England Market and Ontario Market Using a Novel ANN. Int. J. Res. Emerg. Sci. Technol. 2015, 2, 30–40. [Google Scholar]
- Bala, A.; Yadav, N.K. Load Forecasting For Weekend Load Using ANN Technique in Deregulated Environment. IOSR J. Electr. Electron. Eng. 2014, 9, 1–6. [Google Scholar]
- Dilhani, M.H.M.R.S.; Jeenanunta, C. Daily Electric Load Forecasting: Case of Thailand. In Proceedings of the 7th International Conference on Information Communication Technology for Embedded Systems 2016, IC-ICTES, Bangkok, Thailand, 20–22 March 2016; pp. 25–29. [Google Scholar]
- Raza, M.Q.; Baharudin, Z.; Badar-Ul-Islam; Azman Zakariya, M.; Khir, M.H.M. Neural Network Based STLF Model to Study the Seasonal Impact of Weather and Exogenous Variables. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3729–3735. [Google Scholar] [CrossRef]
- Sahay, K.B.; Tripathi, M.M. Day Ahead Hourly Load Forecast of PJM Electricity Market and Iso New England Market by Using Artificial Neural Network. In Proceedings of the ISGT 2014, Istanbul, Turkiye, 12–15 October 2014; pp. 1–5. [Google Scholar]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Álvarez-Bel, C.; Roldán-Porta, C.; Rodríguez-García, J. Upgrade of an Artificial Neural Network Prediction Method for Electrical Consumption Forecasting Using an Hourly Temperature Curve Model. Energy Build. 2013, 60, 38–46. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The Daily and Hourly Energy Consumption and Load Forecasting Using Artificial Neural Network Method: A Case Study Using a Set of 93 Households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef] [Green Version]
- Sahay, K.B.; Sahu, S.; Singh, P. Short-Term Load Forecasting of Toronto Canada by Using Different ANN Algorithms. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Alhmoud, L.; Abu Khurma, R.; Al-Zoubi, A.M.; Aljarah, I. A Real-Time Electrical Load Forecasting in Jordan Using an Enhanced Evolutionary Feedforward Neural Network. Sensors 2021, 21, 6240. [Google Scholar] [CrossRef]
- Liao, Z.; Pan, H.; Huang, X.; Mo, R.; Fan, X.; Chen, H.; Liu, L.; Li, Y. Short-Term Load Forecasting with Dense Average Network. Expert Syst. Appl. 2021, 186, 115748. [Google Scholar] [CrossRef]
- Ding, M.; Wang, L.; Bi, R. An ANN-Based Approach for Forecasting the Power Output of Photovoltaic System. Procedia Environ. Sci. 2011, 11, 1308–1315. [Google Scholar]
- Salgado, R.M.; Ohishi, T.; Ballini, R. A Short-Term Bus Load Forecasting System. In Proceedings of the 2010 10th International Conference on Hybrid Intelligent Systems, Atlanta, GA, USA, 23–25 August 2010; pp. 55–60. [Google Scholar]
- Hernandez, L.; Baladron, C.; Aguiar, J.; Carro, B.; Sanchez-Esguevillas, A.; Lloret, J.; Chinarro, D.; Gomez-Sanz, J.; Cook, D. A Multi-Agent System Architecture for Smart Grid Management and Forecasting of Energy Demand in Virtual Power Plants. IEEE Commun. Mag. 2013, 51, 106–113. [Google Scholar] [CrossRef]
- Alamin, Y.I.; Álvarez, J.D.; del Mar Castilla, M.; Ruano, A. An Artificial Neural Network (ANN) Model to Predict the Electric Load Profile for an HVAC System. IFAC PapersOnLine 2018, 51, 26–31. [Google Scholar] [CrossRef]
- González-Romera, E.; Jaramillo-Morán, M.Á.; Carmona-Fernández, D. Monthly Electric Energy Demand Forecasting Based on Trend Extraction. IEEE Trans. Power Syst. 2006, 21, 1946–1953. [Google Scholar] [CrossRef]
- Johannesen, N.J.; Kolhe, M.; Goodwin, M. Relative Evaluation of Regression Tools for Urban Area Electrical Energy Demand Forecasting. J. Clean. Prod. 2019, 218, 555–564. [Google Scholar] [CrossRef]
- Zhang, W.; Quan, H.; Srinivasan, D. Parallel and Reliable Probabilistic Load Forecasting via Quantile Regression Forest and Quantile Determination. Energy 2018, 160, 810–819. [Google Scholar] [CrossRef]
- Lusis, P.; Khalilpour, K.R.; Andrew, L.; Liebman, A. Short-Term Residential Load Forecasting: Impact of Calendar Effects and Forecast Granularity. Appl. Energy 2017, 205, 654–669. [Google Scholar] [CrossRef]
- Vantuch, T.; Vidal, A.G.; Ramallo-Gonzalez, A.P.; Skarmeta, A.F.; Misak, S. Machine Learning Based Electric Load Forecasting for Short and Long-Term Period. In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018; pp. 511–516. [Google Scholar]
- Bessec, M.; Fouquau, J. Short-Run Electricity Load Forecasting with Combinations of Stationary Wavelet Transforms. Eur. J. Oper. Res. 2018, 264, 149–164. [Google Scholar] [CrossRef]
- Mughees, N.; Mohsin, S.A.; Mughees, A.; Mughees, A. Deep Sequence to Sequence Bi-LSTM Neural Networks for Day-Ahead Peak Load Forecasting. Expert Syst. Appl. 2021, 175, 114844. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No Free Lunch Theorem: A Review. Approx. Optim. 2019, 145, 57–82. [Google Scholar] [CrossRef]
- Ahmia, O.; Farah, N. Multi-Model Approach for Electrical Load Forecasting. In Proceedings of the 2015 SAI Intelligent Systems Conference (IntelliSys), London, UK, 10–11 November 2015; pp. 87–92. [Google Scholar] [CrossRef]
- Zeng, P.; Jin, M.; Elahe, M.F. Short-Term Power Load Forecasting Based on Cross Multi-Model and Second Decision Mechanism. IEEE Access 2020, 8, 184061–184072. [Google Scholar] [CrossRef]
- Peng, C.; Tao, Y.; Chen, Z.; Zhang, Y.; Sun, X. Multi-Source Transfer Learning Guided Ensemble LSTM for Building Multi-Load Forecasting. Expert Syst. Appl. 2022, 202, 117194. [Google Scholar] [CrossRef]
- Li, S.; Zhong, Y.; Lin, J. AWS-DAIE: Incremental Ensemble Short-Term Electricity Load Forecasting Based on Sample Domain Adaptation. Sustainability 2022, 14, 14205. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. A Novel Nonlinear Ensemble Forecasting Model Incorporating GLAR and ANN for Foreign Exchange Rates. Comput. Oper. Res. 2005, 32, 2523–2541. [Google Scholar] [CrossRef]
- De Mattos Neto, P.S.G.; De Oliveira, J.F.L.; Bassetto, P.; Siqueira, H.V.; Barbosa, L.; Pereira Alves, E.; Marinho, M.H.N.; Rissi, G.F.; Li, F.; Oliveira, J.F.L.; et al. Energy Consumption Forecasting for Smart Meters Using Extreme Learning Machine Ensemble. Sensors 2021, 21, 8096. [Google Scholar] [CrossRef]
- Hu, Y.; Qu, B.; Wang, J.; Liang, J.; Wang, Y.; Yu, K.; Li, Y.; Qiao, K. Short-Term Load Forecasting Using Multimodal Evolutionary Algorithm and Random Vector Functional Link Network Based Ensemble Learning. Appl. Energy 2021, 285, 116415. [Google Scholar] [CrossRef]
- Duan, Q.; Liu, J.; Zhao, D. Short Term Electric Load Forecasting Using an Automated System of Model Choice. Int. J. Electr. Power Energy Syst. 2017, 91, 92–100. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, W.; Zhu, K.; Zhou, D.; Dai, H.; Wu, Q. A Novel Trilinear Deep Residual Network with Self-Adaptive Dropout Method for Short-Term Load Forecasting. Expert Syst. Appl. 2021, 182, 115272. [Google Scholar] [CrossRef]
- Gao, R.; Du, L.; Suganthan, P.N.; Zhou, Q.; Yuen, K.F. Random Vector Functional Link Neural Network Based Ensemble Deep Learning for Short-Term Load Forecasting. Expert Syst. Appl. 2022, 206, 117784. [Google Scholar] [CrossRef]
- Saviozzi, M.; Massucco, S.; Silvestro, F. Implementation of Advanced Functionalities for Distribution Management Systems: Load Forecasting and Modeling through Artificial Neural Networks Ensembles. Electr. Power Syst. Res. 2019, 167, 230–239. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; Balding, D.J., Cressie, N.A.C., Fitzmaurice, G.M., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-0-470-54281-1. [Google Scholar]
- Zhang, Z.; Xu, Y.; Yang, J.; Li, X.; Zhang, D. A Survey of Sparse Representation: Algorithms and Applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993. [Google Scholar]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef] [Green Version]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Supervised Dictionary Learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online Dictionary Learning for Sparse Coding. In Proceedings of the ACM International Conference Proceeding Series, Athens, Greece, 29–31 October 2009. [Google Scholar]
- Engan, K.; Aase, S.O.; Husoy, J.H. Method of Optimal Directions for Frame Design. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings. ICASSP99, Phoenix, AZ, USA, 15–19 March 1999. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kyriakides, E.; Polycarpou, M. Short Term Electric Load Forecasting: A Tutorial. Trends Neural Comput. 2006, 35, 391–418. [Google Scholar] [CrossRef]
- Hong, W.C. Intelligent Energy Demand Forecasting; Springer: London, UK, 2013; Volume 10. [Google Scholar]
- Alexandridis, A.; Chondrodima, E.; Giannopoulos, N.; Sarimveis, H. A Fast and Efficient Method for Training Categorical Radial Basis Function Networks. IEEE Trans. Neural Networks Learn. Syst. 2017, 28, 2831–2836. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; John Wiley and Sons: Hoboken, NJ, USA, 2017; ISBN 9781351460491. [Google Scholar]
- Tan, Z.; Zhang, J.; He, Y.; Zhang, Y.; Xiong, G.; Liu, Y. Short-Term Load Forecasting Based on Integration of SVR and Stacking. IEEE Access 2020, 8, 227719–227728. [Google Scholar] [CrossRef]
- Zulfiqar, M.; Gamage, K.A.A.; Kamran, M.; Rasheed, M.B. Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting. Sensors 2022, 22, 4446. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Alexandridis, A.; Chondrodima, E.; Sarimveis, H. Radial Basis Function Network Training Using a Nonsymmetric Partition of the Input Space and Particle Swarm Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 219–230. [Google Scholar] [CrossRef]
- Papadimitrakis, M.; Alexandridis, A. Active Vehicle Suspension Control Using Road Preview Model Predictive Control and Radial Basis Function Networks. Appl. Soft Comput. 2022, 120, 108646. [Google Scholar] [CrossRef]
- Karamichailidou, D.; Alexandridis, A.; Anagnostopoulos, G.; Syriopoulos, G.; Sekkas, O. Modeling Biogas Production from Anaerobic Wastewater Treatment Plants Using Radial Basis Function Networks and Differential Evolution. Comput. Chem. Eng. 2022, 157, 107629. [Google Scholar] [CrossRef]
- Chondrodima, E.; Georgiou, H.; Pelekis, N.; Theodoridis, Y. Particle Swarm Optimization and RBF Neural Networks for Public Transport Arrival Time Prediction Using GTFS Data. Int. J. Inf. Manag. Data Insights 2022, 2, 100086. [Google Scholar] [CrossRef]
- Karamichailidou, D.; Kaloutsa, V.; Alexandridis, A. Wind Turbine Power Curve Modeling Using Radial Basis Function Neural Networks and Tabu Search. Renew. Energy 2021, 163, 2137–2152. [Google Scholar] [CrossRef]
- Sun, L.; Zhou, K.; Zhang, X.; Yang, S. Outlier Data Treatment Methods Toward Smart Grid Applications. IEEE Access 2018, 6, 39849–39859. [Google Scholar] [CrossRef]
- Martín, P.; Moreno, G.; Rodríguez, F.J.; Jiménez, J.A.; Fernández, I. A Hybrid Approach to Short-Term Load Forecasting Aimed at Bad Data Detection in Secondary Substation Monitoring Equipment. Sensors 2018, 18, 3947. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Sun, S.; Chen, X.; Zeng, X.; Kong, Y.; Chen, J.; Guo, Y.; Wang, T. Short-Term Load Forecasting of Industrial Customers Based on SVMD and XGBoost. Int. J. Electr. Power Energy Syst. 2021, 129, 106830. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Wang, S.; Wang, D. Bi-Directional Long Short-Term Memory Method Based on Attention Mechanism and Rolling Update for Short-Term Load Forecasting. Int. J. Electr. Power Energy Syst. 2019, 109, 470–479. [Google Scholar] [CrossRef]
- Javed, U.; Ijaz, K.; Jawad, M.; Khosa, I.; Ahmad Ansari, E.; Shabih Zaidi, K.; Nadeem Rafiq, M.; Shabbir, N. A Novel Short Receptive Field Based Dilated Causal Convolutional Network Integrated with Bidirectional LSTM for Short-Term Load Forecasting. Expert Syst. Appl. 2022, 205, 117689. [Google Scholar] [CrossRef]
- Román-Portabales, A.; López-Nores, M.; Pazos-Arias, J.J. Systematic Review of Electricity Demand Forecast Using ANN-Based Machine Learning Algorithms. Sensors 2021, 21, 4544. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Alhuyi Nazari, M.; Mahariq, I.; Ali, N. Modeling and Sensitivity Analysis of Thermal Conductivity of Ethylene Glycol-Water Based Nanofluids with Alumina Nanoparticles. Exp. Tech. 2023, 47, 83–90. [Google Scholar] [CrossRef]
- Zhou, B.; Meng, Y.; Huang, W.; Wang, H.; Deng, L.; Huang, S.; Wei, J. Multi-Energy Net Load Forecasting for Integrated Local Energy Systems with Heterogeneous Prosumers. Int. J. Electr. Power Energy Syst. 2021, 126, 106542. [Google Scholar] [CrossRef]











| Prediction Horizon | 15 min | 1 h | 2 h | 3 h | 6 h | 24 h |
|---|---|---|---|---|---|---|
| Current and past AP measures | ||||||
| Average AP measures | ||||||
| Difference AP measures | ||||||
| Weather measures | ||||||
| Future AP forecasts (output variable) |
| Method | R2 | ΜAΕ | RMSE | Rank1 |
|---|---|---|---|---|
| 15 min | ||||
| Proposed | 0.98613 | 0.26120 | 0.4703 | - |
| MLP ensemble | 0.9852 | 0.2760 | 0.4869 | - |
| MLP | 0.98568 | 0.26936 | 0.4782 | 19.25% |
| RBF | 0.98574 | 0.27095 | 0.4773 | 19.94% |
| LR | 0.98562 | 0.26700 | 0.4793 | 10.49% |
| SVR | 0.98541 | 0.26931 | 0.4829 | 14.23% |
| RF | 0.98373 | 0.29531 | 0.5071 | 24.27% |
| SR | 0.98561 | 0.26715 | 0.4795 | 11.82% |
| 1 h | ||||
| Proposed | 0.93793 | 0.60224 | 0.9946 | - |
| MLP ensemble | 0.9344 | 0.6330 | 1.0240 | - |
| MLP | 0.91697 | 0.66794 | 1.1500 | 21.56% |
| RBF | 0.93253 | 0.64235 | 1.0374 | 20.77% |
| LR | 0.93168 | 0.64174 | 1.0438 | 8.91% |
| SVR | 0.93008 | 0.65376 | 1.0562 | 10.70% |
| RF | 0.92912 | 0.67311 | 1.0614 | 20.79% |
| SR | 0.93045 | 0.64079 | 1.0532 | 17.27% |
| 2 h | ||||
| Proposed | 0.88147 | 0.88279 | 1.3767 | - |
| MLP ensemble | 0.8838 | 0.8965 | 1.3721 | - |
| MLP | 0.84455 | 0.99479 | 1.5854 | 20.32% |
| RBF | 0.87052 | 0.96255 | 1.4472 | 18.32% |
| LR | 0.87233 | 0.93356 | 1.4377 | 11.20% |
| SVR | 0.86949 | 0.93765 | 1.4537 | 11.38% |
| RF | 0.86653 | 0.96596 | 1.4675 | 22.94% |
| SR | 0.86953 | 0.93189 | 1.4534 | 15.92% |
| 3 h | ||||
| Proposed | 0.84143 | 1.0599 | 1.5871 | - |
| MLP ensemble | 0.8359 | 1.0859 | 1.6192 | - |
| MLP | 0.78486 | 1.2504 | 1.8538 | 18.08% |
| RBF | 0.82483 | 1.1367 | 1.6727 | 20.14% |
| LR | 0.82241 | 1.1270 | 1.6843 | 8.74% |
| SVR | 0.81914 | 1.1512 | 1.6997 | 11.82% |
| RF | 0.81895 | 1.1391 | 1.7006 | 23.67% |
| SR | 0.81893 | 1.1229 | 1.7007 | 17.54% |
| 6 h | ||||
| Proposed | 0.83251 | 1.1144 | 1.6462 | - |
| MLP ensemble | 0.8272 | 1.1951 | 1.6888 | - |
| MLP | 0.83036 | 1.1758 | 1.6733 | 20.77% |
| RBF | 0.80289 | 1.2848 | 1.8037 | 21.31% |
| LR | 0.77800 | 1.3308 | 1.9141 | 10.34% |
| SVR | 0.75400 | 1.4300 | 2.0150 | 16.42% |
| RF | 0.81341 | 1.2119 | 1.7549 | 21.08% |
| SR | 0.77373 | 1.3413 | 1.9325 | 10.08% |
| 24 h | ||||
| Proposed | 0.78474 | 1.1835 | 1.8174 | - |
| MLP ensemble | 0.7827 | 1.2372 | 1.8468 | - |
| MLP | 0.78073 | 1.2313 | 1.8553 | 21.93% |
| RBF | 0.73576 | 1.4119 | 2.0367 | 21.83% |
| LR | 0.75712 | 1.3188 | 1.9526 | 11.16% |
| SVR | 0.73669 | 1.3031 | 2.0331 | 16.82% |
| RF | 0.76487 | 1.2694 | 1.9212 | 16.71% |
| SR | 0.74761 | 1.3419 | 1.9905 | 11.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giamarelos, N.; Papadimitrakis, M.; Stogiannos, M.; Zois, E.N.; Livanos, N.-A.I.; Alexandridis, A. A Machine Learning Model Ensemble for Mixed Power Load Forecasting across Multiple Time Horizons. Sensors 2023, 23, 5436. https://doi.org/10.3390/s23125436
Giamarelos N, Papadimitrakis M, Stogiannos M, Zois EN, Livanos N-AI, Alexandridis A. A Machine Learning Model Ensemble for Mixed Power Load Forecasting across Multiple Time Horizons. Sensors. 2023; 23(12):5436. https://doi.org/10.3390/s23125436
Chicago/Turabian StyleGiamarelos, Nikolaos, Myron Papadimitrakis, Marios Stogiannos, Elias N. Zois, Nikolaos-Antonios I. Livanos, and Alex Alexandridis. 2023. "A Machine Learning Model Ensemble for Mixed Power Load Forecasting across Multiple Time Horizons" Sensors 23, no. 12: 5436. https://doi.org/10.3390/s23125436