Frequency Stability Prediction of Power Systems Using Vision Transformer and Copula Entropy
Abstract
:1. Introduction
2. Related Work
2.1. Model-Driven Methods
2.2. Data-Driven Methods
2.3. Transformer Models in DL
2.4. Feature Selection Methods
2.5. Frequency Security Indices
2.6. Our Contributions
- This paper proposes a ViT-based FSP method that predicts frequency security online following a disturbance.
- A CE-based feature selection method is used to construct image-like data with fixed dimensions, which can decrease the computational burden of the proposed model by removing redundant information.
- This paper develops a novel FSI as the predicted result of the model, which considers the safety margin and comprehensive characteristics of frequency compared with the traditional indicators.
- Case studies are conducted on a modified IEEE 39-bus system and a modified ACTIVSg500 system for projected 0% to 40% nonsynchronous system penetration levels, aiming to validate the proposed method’s efficacy and scalability.
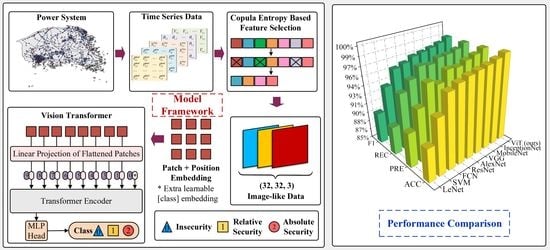
3. ViT-Based FSP Method
3.1. Vision Transformer (ViT)
3.1.1. Multihead Self-Attention
3.1.2. ViT
3.2. CE-Based Feature Selection
- (1)
- Estimating the empirical copula density (ECD)
- (2)
- Estimating the CE
3.3. Frequency Security Index
3.3.1. Center-of-Inertia Frequency
3.3.2. Insecure Boundaries and Secure Boundaries
3.3.3. Calculation of the FSI
4. Overall Process of the Proposed Method
4.1. Raw Database
4.2. Offline Training
4.3. Online Application
4.4. Evaluation Indicators
4.5. Equipment and Software
5. Case Studies
5.1. A Modified New England 39-Bus System
5.1.1. Feature Subset
5.1.2. Performance Comparison
5.1.3. Influence of Gaussian Noise
5.1.4. Incomplete Data Analysis
5.1.5. Visualization Analysis of the ViT
5.2. A Modified ACTIVSg500 System
Testing Results and Comparison
6. Discussion
7. Conclusions and Future Work
- The ViT-based FSP method achieves SOTA performance compared to eight ML methods on normal, noisy, and incomplete datasets, so the proposed method is suitable for practical applications.
- As for the FSP of power systems tasks, the global feature extraction of MSA is a better mechanism than the local feature extraction of convolution.
- When using CE-based feature selection, the proposed method is still efficient and achieves high performance in power systems of any scale without vast computational resources.
- From the point of view of CE, the apparent power of the transmission line and the voltage phase angle of the bus have strong correlations with FSP when the load variance occurs. Conversely, the active power of the generator has a weak correlation with FSP when the load variance occurs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| #1 | #2 | #3 | #4 | #5 | #6 | #7 |
| 0.20 | 0.0 | 0.0 | 0.0 | 0.10 | 1.50 | 0.50 |
| #8 | #9 | #10 | #11 | #12 | #13 | |
| 0.90 | 1.0 | 1.20 | 2.0 | 5.0 | 0.02 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
| 1.25 | 4.95 | 0.0 | 0.7 × 10−2 | 21.98 | 0.0 | 1.8 | 1.5 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
| 0.30 | 150.0 | 25.0 | 3.0 | 30.0 | 0.0 | 27.0 | 10.0 | 1.0 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
| 0.15 | 18.0 | 5.0 | 0.0 | 0.05 | 3.0 | 0.60 | 1.12 |
| #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 |
| 0.10 | 0.296 | −0.436 | 1.10 | 0.05 | 0.45 | −0.45 | 5.0 |
| #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 |
| 0.05 | 0.90 | 1.20 | 40.0 | −0.50 | 0.40 | 0.05 | 0.05 |
| #25 | #26 | #27 | #28 | #29 | #30 | #31 | |
| 1.0 | 0.69 | 0.78 | 0.98 | 1.12 | 0.74 | 1.20 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 |
| 0.2 × 10−1 | 10.0 | 0.90 | 0.50 | 1.22 | 1.20 | 0.80 |
| #8 | #9 | #10 | #11 | #12 | #13 | #14 |
| 0.40 | −1.30 | 0.2 × 10−1 | 0.70 | 9999.0 | −9999.0 | 1.0 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
| −99.0 | 99.0 | 0.0 | −0.5 × 10−1 | 0.5e-0.1 | 0.0 | 1.05 | −1.05 | 0.0 |
| #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 |
| 0.5 × 10−1 | 0.436 | −0.436 | 1.10 | 0.90 | 0.0 | 0.10 | 0.0 | 40.0 |
| #19 | #20 | #21 | #22 | #23 | #24 | #25 | ||
| 0.2 × 10−1 | 99.0 | −99.0 | 1.0 | 0.0 | 1.82 | 0.2 × 10−1 |
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
| 0.2 × 10−1 | 18.0 | 5.0 | 0.0 | 0.75 × 10−1 | 0.0 | 0.0 | 0.0 | 0.2 × 10−1 |
| #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 |
| 0.10 | −0.10 | 0.0 | 0.0 | 0.436 | −0.436 | 0.10 | 0.5 × 10−1 | 0.25 |
| #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 |
| 0.0 | 0.0 | 999.0 | −999.0 | 999.0 | −999.0 | 0.10 | 20.0 | 0.0 |
References
- Arora, N.K.; Mishra, I. COP26: More Challenges than Achievements. Environ. Sustain. 2021, 4, 585–588. [Google Scholar] [CrossRef]
- Jin, T.; Kim, J. What Is Better for Mitigating Carbon Emissions–Renewable Energy or Nuclear Energy? A Panel Data Analysis. Renew. Sustain. Energy Rev. 2018, 91, 464–471. [Google Scholar] [CrossRef]
- Qin, B.; Wang, M.; Zhang, G.; Zhang, Z. Impact of Renewable Energy Penetration Rate on Power System Frequency Stability. Energy Rep. 2022, 8, 997–1003. [Google Scholar] [CrossRef]
- Homan, S.; Mac Dowell, N.; Brown, S. Grid Frequency Volatility in Future Low Inertia Scenarios: Challenges and Mitigation Options. Appl. Energy 2021, 290, 116723. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Cheng, Y.; Azizipanah-Abarghooee, R.; Azizi, S.; Ding, L.; Terzija, V. Smart Frequency Control in Low Inertia Energy Systems Based on Frequency Response Techniques: A Review. Appl. Energy 2020, 279, 115798. [Google Scholar] [CrossRef]
- Shazon, M.N.H.; Jawad, A. Frequency Control Challenges and Potential Countermeasures in Future Low-Inertia Power Systems: A Review. Energy Rep. 2022, 8, 6191–6219. [Google Scholar] [CrossRef]
- Yu, J.; Liao, S.; Xu, J. Frequency Control Strategy for Coordinated Energy Storage System and Flexible Load in Isolated Power System. Energy Rep. 2022, 8, 966–979. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, R.; Ashfaq, H.; Sharma, S.K.; Sharma, G.; Bokoro, P.N. Super-Twisting Algorithm-Based Virtual Synchronous Generator in Inverter Interfaced Distributed Generation (IIDG). Energies 2022, 15, 5890. [Google Scholar] [CrossRef]
- Mohseni, N.A.; Bayati, N. Robust Multi-Objective H2/H∞ Load Frequency Control of Multi-Area Interconnected Power Systems Using TS Fuzzy Modeling by Considering Delay and Uncertainty. Energies 2022, 15, 5525. [Google Scholar] [CrossRef]
- Tan, Y.; Muttaqi, K.M.; Ciufo, P.; Meegahapola, L.; Guo, X.; Chen, B.; Chen, H. Enhanced Frequency Regulation Using Multilevel Energy Storage in Remote Area Power Supply Systems. IEEE Trans. Power Syst. 2018, 34, 163–170. [Google Scholar] [CrossRef]
- Vaish, R.; Dwivedi, U.D.; Tewari, S.; Tripathi, S.M. Machine Learning Applications in Power System Fault Diagnosis: Research Advancements and Perspectives. Eng. Appl. Artif. Intell. 2021, 106, 104504. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, G.; Hu, W.; Cao, D.; Li, J.; Xu, S.; Xu, D.; Chen, Z. Artificial Intelligence Based Approach to Improve the Frequency Control in Hybrid Power System. Energy Rep. 2020, 6, 174–181. [Google Scholar] [CrossRef]
- Wen, Y.; Li, W.; Huang, G.; Liu, X. Frequency Dynamics Constrained Unit Commitment with Battery Energy Storage. IEEE Trans. Power Syst. 2016, 31, 5115–5125. [Google Scholar] [CrossRef]
- Nguyen, N.; Almasabi, S.; Bera, A.; Mitra, J. Optimal Power Flow Incorporating Frequency Security Constraint. IEEE Trans. Ind. Appl. 2019, 55, 6508–6516. [Google Scholar] [CrossRef]
- Mohajeryami, S.; Neelakantan, A.R.; Moghaddam, I.N.; Salami, Z. Modeling of Deadband Function of Governor Model and Its Effect on Frequency Response Characteristics. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Sigrist, L.; Egido, I.; Miguélez, E.L.; Rouco, L. Sizing and Controller Setting of Ultracapacitors for Frequency Stability Enhancement of Small Isolated Power Systems. IEEE Trans. Power Syst. 2014, 30, 2130–2138. [Google Scholar] [CrossRef]
- Chan, M.L.; Dunlop, R.D.; Schweppe, F. Dynamic Equivalents for Average System Frequency Behavior Following Major Distribances. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 1637–1642. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Lin, J.; Teng, Y. A Hybrid Equivalent Model for Prediction of Power System Frequency Response. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Anderson, P.M.; Mirheydar, M. A Low-Order System Frequency Response Model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Sun, L.; Yuan, X.; Wang, S.; Chi, Y. Modeling of Type 3 Wind Turbines with Df/Dt Inertia Control for System Frequency Response Study. IEEE Trans. Power Syst. 2016, 32, 2799–2809. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Zhang, Y.; Xie, Y.; Ma, C. Extending SFR Model to Incorporate the Influence of Thermal States on Primary Frequency Response. IET Gener. Transm. Distrib. 2020, 14, 4069–4078. [Google Scholar] [CrossRef]
- Gadde, P.H.; Biswal, M.; Brahma, S.; Cao, H. Efficient Compression of PMU Data in WAMS. IEEE Trans. Smart Grid 2016, 7, 2406–2413. [Google Scholar] [CrossRef]
- Persson, M.; Chen, P. Frequency Evaluation of the Nordic Power System Using PMU Measurements. IET Gener. Transm. Distrib. 2017, 11, 2879–2887. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, X.; Zhang, H.; Cao, Y.; Terzija, V. Review on Deep Learning Applications in Frequency Analysis and Control of Modern Power System. Int. J. Electr. Power Energy Syst. 2022, 136, 107744. [Google Scholar] [CrossRef]
- Yurdakul, O.; Eser, F.; Sivrikaya, F.; Albayrak, S. Very Short-Term Power System Frequency Forecasting. IEEE Access 2020, 8, 141234–141245. [Google Scholar] [CrossRef]
- Shi, Z.; Yao, W.; Zeng, L.; Wen, J.; Fang, J.; Ai, X.; Wen, J. Convolutional Neural Network-Based Power System Transient Stability Assessment and Instability Mode Prediction. Appl. Energy 2020, 263, 114586. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, C.; Zhu, L.; Song, J. Data-Driven Short-Term Voltage Stability Assessment Based on Spatial-Temporal Graph Convolutional Network. Int. J. Electr. Power Energy Syst. 2021, 130, 106753. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Asif, N.A.; Sarker, Y.; Chakrabortty, R.K.; Ryan, M.J.; Ahamed, M.H.; Saha, D.K.; Badal, F.R.; Das, S.K.; Ali, M.F.; Moyeen, S.I. Graph Neural Network: A Comprehensive Review on Non-Euclidean Space. IEEE Access 2021, 9, 60588–60606. [Google Scholar] [CrossRef]
- Xie, J.; Sun, W. A Transfer and Deep Learning-Based Method for Online Frequency Stability Assessment and Control. IEEE Access 2021, 9, 75712–75721. [Google Scholar] [CrossRef]
- Zhan, X.; Han, S.; Rong, N.; Liu, P.; Ao, W. A Two-Stage Transient Stability Prediction Method Using Convolutional Residual Memory Network and Gated Recurrent Unit. Int. J. Electr. Power Energy Syst. 2022, 138, 107973. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Z.; Bian, Z.; Xu, Z. A Short-Term Voltage Stability Online Prediction Method Based on Graph Convolutional Networks and Long Short-Term Memory Networks. Int. J. Electr. Power Energy Syst. 2021, 127, 106647. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Kenton, J.D.M.-W.C.; Toutanova, L.K. Bert: Pre-Training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the NAACL-HLT, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Yan, H.; Zhang, C.; Wu, M. Lawin Transformer: Improving Semantic Segmentation Transformer with Multi-Scale Representations via Large Window Attention. arXiv 2022, arXiv:2201.01615. [Google Scholar]
- Dokeroglu, T.; Deniz, A.; Kiziloz, H.E. A Comprehensive Survey on Recent Metaheuristics for Feature Selection. Neurocomputing 2022, 494, 269–296. [Google Scholar] [CrossRef]
- Niu, T.; Wang, J.; Lu, H.; Yang, W.; Du, P. Developing a Deep Learning Framework with Two-Stage Feature Selection for Multivariate Financial Time Series Forecasting. Expert Syst. Appl. 2020, 148, 113237. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating Mutual Information. Phys. Rev. E 2004, 69, 66138. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Sun, Z. Mutual Information Is Copula Entropy. Tsinghua Sci. Technol. 2011, 16, 51–54. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, D.; Wang, X.; Lin, J. A Method of Frequency Curve Prediction Based on Deep Belief Network of Post-Disturbance Power System. In Proceedings of the CSEE, Rome, Italy, 7–9 April 2019; Volume 39, pp. 5095–5104. [Google Scholar]
- Liu, L.; Li, W.; Ba, Y.; Shen, J.; Jin, C.; Wen, K. An Analytical Model for Frequency Nadir Prediction Following a Major Disturbance. IEEE Trans. Power Syst. 2020, 35, 2527–2536. [Google Scholar] [CrossRef]
- Wen, Y.; Zhao, R.; Huang, M.; Guo, C. Data-driven Transient Frequency Stability Assessment: A Deep Learning Method with Combined Estimation-correction Framework. Energy Convers. Econ. 2020, 1, 198–209. [Google Scholar] [CrossRef]
- Delkhosh, H.; Seifi, H. Power System Frequency Security Index Considering All Aspects of Frequency Profile. IEEE Trans. Power Syst. 2021, 36, 1656–1659. [Google Scholar] [CrossRef]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-Attention with Relative Position Representations. arXiv 2018, arXiv:1803.02155. [Google Scholar]
- Arnab, A.; Dehghani, M.; Heigold, G.; Sun, C.; Lučić, M.; Schmid, C. ViViT: A Video Vision Transformer. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 6816–6826. [Google Scholar]
- Xiong, R.; Yang, Y.; He, D.; Zheng, K.; Zheng, S.; Xing, C.; Zhang, H.; Lan, Y.; Wang, L.; Liu, T. On Layer Normalization in the Transformer Architecture. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual Event, 13–18 July 2020; pp. 10524–10533. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 0387286780. [Google Scholar]
- Sklar, M. Fonctions de Repartition an Dimensions et Leurs Marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Rudez, U.; Mihalic, R. WAMS-Based Underfrequency Load Shedding with Short-Term Frequency Prediction. IEEE Trans. Power Deliv. 2016, 31, 1912–1920. [Google Scholar] [CrossRef]
- Qi, Y.; Deng, H.; Liu, X.; Tang, Y. Synthetic Inertia Control of Grid-Connected Inverter Considering the Synchronization Dynamics. IEEE Trans. Power Electron. 2021, 37, 1411–1421. [Google Scholar] [CrossRef]
- Kushwaha, P.; Prakash, V.; Bhakar, R.; Yaragatti, U.R. Synthetic Inertia and Frequency Support Assessment from Renewable Plants in Low Carbon Grids. Electr. Power Syst. Res. 2022, 209, 107977. [Google Scholar] [CrossRef]
- Riquelme, E.; Chavez, H.; Barbosa, K.A. RoCoF-Minimizing H2 Norm Control Strategy for Multi-Wind Turbine Synthetic Inertia. IEEE Access 2022, 10, 18268–18278. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic Gradient Descent with Warm Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Rodrigues, Y.R.; Abdelaziz, M.; Wang, L.; Kamwa, I. PMU Based Frequency Regulation Paradigm for Multi-Area Power Systems Reliability Improvement. IEEE Trans. Power Syst. 2021, 36, 4387–4399. [Google Scholar] [CrossRef]
- Mohamad, A.M.; Hashim, N.; Hamzah, N.; Ismail, N.F.N.; Latip, M.F.A. Transient Stability Analysis on Sarawak’s Grid Using Power System Simulator for Engineering (PSS/E). In Proceedings of the 2011 IEEE Symposium on Industrial Electronics and Applications, Langkawi, Malaysia, 25–28 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 521–526. [Google Scholar]
- Ellis, A.; Kazachkov, Y.; Muljadi, E.; Pourbeik, P.; Sanchez-Gasca, J.J. Description and Technical Specifications for Generic WTG Models—A Status Report. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- LeCun, Y. LeNet-5, Convolutional Neural Networks. 2015. Available online: http://yann.lecun.com/exdb/lenet/ (accessed on 31 October 2020).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Birchfield, A.B.; Xu, T.; Gegner, K.M.; Shetye, K.S.; Overbye, T.J. Grid Structural Characteristics as Validation Criteria for Synthetic Networks. IEEE Trans. Power Syst. 2016, 32, 3258–3265. [Google Scholar] [CrossRef]
- Zhu, S.; Piper, D.; Ramasubramanian, D.; Quint, R.; Isaacs, A.; Bauer, R. Modeling Inverter-Based Resources in Stability Studies. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef]
- Raghu, M.; Unterthiner, T.; Kornblith, S.; Zhang, C.; Dosovitskiy, A. Do Vision Transformers See like Convolutional Neural Networks? Adv. Neural Inf. Process. Syst. 2021, 34, 12116–12128. [Google Scholar]
- Kazemi, M.V.; Sadati, S.J.; Gholamian, S.A. Adaptive Frequency Control of Microgrid Based on Fractional Order Control and a Data-Driven Control with Stability Analysis. IEEE Trans. Smart Grid 2021, 13, 381–392. [Google Scholar] [CrossRef]
- Peng, Q.; Yang, Y.; Liu, T.; Blaabjerg, F. Coordination of Virtual Inertia Control and Frequency Damping in PV Systems for Optimal Frequency Support. CPSS Trans. Power Electron. Appl. 2020, 5, 305–316. [Google Scholar] [CrossRef]












| Index (φ) | Boundaries | |
|---|---|---|
| SB (φ) | IB (φ) | |
| Δfc | α × Δfcmax | Δfcmax |
| RoCoF | β × RoCoFmax | RoCoFmax |
| Δfs | γ × Δfsmax | Δfsmax |
| Number | Original Feature |
|---|---|
| 1 | Electrical power of each generator from t0 to 32 ft |
| 2 | Active power load of each bus from t0 to 32 ft |
| 3 | Voltage amplitude of each bus from t0 to 32 ft |
| 4 | Voltage phase angle of each bus from t0 to 32 ft |
| 5 | Apparent power of each line from t0 to 32 ft |
| Name | Value |
|---|---|
| Load Levels | 50%, 51%, 52%, …, 100% |
| Fault Buses | 3, 4, 7, 8, 12, 15, 16, 18, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31, 39 |
| Fault Sizes (MW) | −500, −400, −300, −200, 200, 300, 400, 500 |
| REPRs | 0%, 5%, 10%, 15%, 20%, 25%, 30%, 35%, 40% |
| Disturbancemax (MW) | Disturbancemin (MW) | Δfmax (Hz) | |RoCoFmax| (Hz/s) | Δfsdes (Hz) |
|---|---|---|---|---|
| ±400 | ±200 | 0.6 | 0.5 | 0.25 |
| Hyperparameter | Value |
|---|---|
| Input size | 32 |
| Classes | 3 |
| Patch size | 4 |
| Hidden size | 256 |
| Heads | 8 |
| MLP size | 128 |
| Dropout | 0.05 |
| Model | Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 50 dB | 45 dB | 40 dB | 35 dB | 30 dB | 25 dB | 20 dB | 15 dB | 10 dB | |
| SVM | 93.93 | 93.81 | 93.68 | 93.49 | 93.02 | 92.55 | 91.51 | 89.05 | 84.92 |
| FCN | 96.36 | 95.88 | 94.90 | 94.13 | 93.98 | 93.89 | 92.16 | 89.38 | 85.81 |
| LeNet | 89.42 | 89.33 | 89.08 | 88.52 | 87.16 | 86.74 | 85.31 | 84.95 | 82.06 |
| AlexNet | 97.53 | 97.29 | 96.86 | 96.78 | 96.63 | 96.36 | 94.78 | 90.23 | 82.31 |
| InceptionNet | 98.16 | 98.08 | 97.87 | 97.39 | 96.98 | 96.33 | 95.22 | 94.02 | 90.29 |
| VGG | 97.55 | 97.24 | 97.07 | 96.86 | 96.61 | 95.91 | 95.34 | 93.49 | 89.16 |
| ResNet | 97.27 | 97.08 | 96.78 | 96.58 | 96.26 | 95.82 | 95.04 | 92.16 | 90.15 |
| MobileNet | 97.81 | 97.76 | 97.72 | 97.35 | 96.94 | 96.35 | 94.24 | 90.14 | 81.37 |
| ViT (ours) | 98.86 | 98.54 | 98.39 | 98.21 | 97.97 | 97.42 | 96.56 | 94.79 | 90.94 |
| Model | Accuracy (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | |
| SVM | 87.29 | 84.44 | 82.65 | 80.76 | 79.16 | 77.57 | 76.60 | 75.72 |
| FCN | 87.98 | 85.08 | 83.14 | 81.31 | 80.55 | 79.13 | 78.19 | 76.93 |
| LeNet | 84.49 | 83.06 | 82.84 | 80.88 | 79.66 | 79.59 | 79.28 | 79.18 |
| AlexNet | 92.25 | 87.62 | 84.57 | 79.47 | 77.61 | 75.33 | 73.58 | 71.44 |
| InceptionNet | 96.06 | 95.29 | 94.48 | 93.11 | 91.79 | 90.76 | 89.89 | 89.78 |
| VGG | 94.91 | 93.04 | 90.83 | 90.16 | 87.92 | 86.24 | 85.48 | 83.82 |
| ResNet | 96.63 | 95.46 | 94.78 | 93.78 | 92.98 | 91.54 | 90.49 | 89.97 |
| MobileNet | 87.77 | 86.27 | 80.34 | 76.02 | 72.08 | 71.76 | 69.03 | 67.76 |
| ViT (ours) | 97.11 | 95.86 | 95.08 | 94.95 | 94.32 | 93.62 | 92.54 | 90.78 |
| Name | Value |
|---|---|
| Load Levels | 50%, 52%, 54%, …, 100% |
| Fault Buses | 4, 6, 61, 64, 103, 150, 204, 292, 303, 364, 470, 499 |
| Fault Sizes (MW) | −700, −600, −500, −400, −300, −200, −100, 100, 200, 300, 400, 500, 600, 700 |
| REPRs | 0%, 5%, 10%, 15%, 20%, 25%, 30%, 35%, 40% |
| Disturbancemax (MW) | Disturbancemin (MW) | Δfmax (Hz) | |RoCoFmax| (Hz/s) | Δfsdes (Hz) |
|---|---|---|---|---|
| ±550 | ±250 | 1 | 1 | 0.4 |
| Model | Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 50 dB | 45 dB | 40 dB | 35 dB | 30 dB | 25 dB | 20 dB | 15 dB | 10 dB | |
| SVM | 92.21 | 92.18 | 92.04 | 91.89 | 91.54 | 90.32 | 89.42 | 88.21 | 85.43 |
| FCN | 96.65 | 96.31 | 96.01 | 95.87 | 95.10 | 94.95 | 92.27 | 90.43 | 87.66 |
| LeNet | 88.31 | 87.47 | 87.31 | 86.71 | 86.98 | 86.85 | 86.69 | 85.71 | 84.62 |
| AlexNet | 97.22 | 96.52 | 96.33 | 96.16 | 95.23 | 94.91 | 92.76 | 89.62 | 86.41 |
| InceptionNet | 98.63 | 98.53 | 98.48 | 98.08 | 97.79 | 95.41 | 93.82 | 91.39 | 88.99 |
| VGG | 98.82 | 98.57 | 98.55 | 98.31 | 97.86 | 96.33 | 94.12 | 90.54 | 88.38 |
| ResNet | 98.94 | 98.69 | 98.48 | 97.94 | 97.29 | 95.49 | 93.13 | 90.97 | 88.49 |
| MobileNet | 98.96 | 98.68 | 98.30 | 97.09 | 95.28 | 92.83 | 90.89 | 88.92 | 85.17 |
| ViT (ours) | 99.12 | 99.04 | 98.96 | 98.48 | 98.37 | 97.47 | 95.46 | 91.97 | 89.55 |
| Model | Accuracy (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | |
| SVM | 90.78 | 90.16 | 89.73 | 89.02 | 88.76 | 88.23 | 87.75 | 87.36 |
| FCN | 89.55 | 88.09 | 86.69 | 86.47 | 86.02 | 85.67 | 84.95 | 84.57 |
| LeNet | 85.21 | 84.95 | 84.00 | 83.57 | 82.75 | 82.66 | 81.97 | 81.89 |
| AlexNet | 91.59 | 88.88 | 86.87 | 86.71 | 85.33 | 85.04 | 84.25 | 83.69 |
| InceptionNet | 94.03 | 91.11 | 90.81 | 90.12 | 89.85 | 88.99 | 88.32 | 87.87 |
| VGG | 92.73 | 91.45 | 90.27 | 89.84 | 88.84 | 88.26 | 87.47 | 87.18 |
| ResNet | 94.47 | 92.17 | 91.11 | 90.24 | 89.32 | 88.66 | 88.13 | 87.70 |
| MobileNet | 89.77 | 88.35 | 86.87 | 85.72 | 85.23 | 84.25 | 83.42 | 83.25 |
| ViT (ours) | 95.04 | 93.23 | 92.74 | 91.27 | 90.95 | 90.36 | 89.98 | 89.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Han, S.; Rong, N.; Fan, J. Frequency Stability Prediction of Power Systems Using Vision Transformer and Copula Entropy. Entropy 2022, 24, 1165. https://doi.org/10.3390/e24081165
Liu P, Han S, Rong N, Fan J. Frequency Stability Prediction of Power Systems Using Vision Transformer and Copula Entropy. Entropy. 2022; 24(8):1165. https://doi.org/10.3390/e24081165
Chicago/Turabian StyleLiu, Peili, Song Han, Na Rong, and Junqiu Fan. 2022. "Frequency Stability Prediction of Power Systems Using Vision Transformer and Copula Entropy" Entropy 24, no. 8: 1165. https://doi.org/10.3390/e24081165