The Energetics and Topology of Grain Boundaries in Magnesium: An Ab Initio Study

Abstract

First principles calculations were carried out on six different grain boundaries with complex, non-symmetrical, crystallography’s. Solute species (Gd and Zn) were placed in multiple locations to investigate their effect on the boundary energetics. The grain boundaries were found to have an intrinsic grain boundary energy, and this energy was not markedly affected by the solute concentration at the boundary. However, the work of separation (W_SEP) was very sensitive to grain boundary chemistry. Boundaries of higher disorder were found to be more sensitive to boundary chemistry and showed higher values of W_SEP and in the case of Gd, were more sensitive to solute concentration at the boundary. No correlation between the boundary behaviour and crystallography could be found, apart from the over-riding conclusion that all six boundaries showed markedly different behaviours, and the effect of solute on each were unique.

1. Introduction

In polycrystalline materials grains form a network of grain boundaries [1], which determine the materials response to external fields [2,3]. Grain boundaries are characterized by five macroscopic degrees of freedom consisting of the rotation axis, the normal to the interface plane and the rotation angle [4]. The rotation axis and the boundary normal can be either perpendicular to, or parallel with each other. The former case is referred to as a tilt boundary and the latter, is called a twist grain boundary. In most cases, boundaries are neither perfectly twist or tilt in character, but are mixed. Although some boundaries show symmetry across the boundary interface, again this is not very common and asymmetrical grain boundaries [5] constitute a significant fraction of boundaries in real materials [6]. In addition to their crystallography, boundaries can also contain chemistries different to the bulk. In the case of magnesium, the segregation of elements with large atomic radii such as the rare earth (RE) elements have been shown to be quite strong. This topic is of particular interest because these elements are strong texture modifiers during recrystallisation, and this is attributed to their interaction with grain boundaries.

It has been found that the RE elements segregate to dislocations [7] and grain boundaries [8,9,10,11,12,13,14,15,16,17,18], and it has also been shown that elemental pair such as Gd and Zn are found to co-segregate [8]. It has been suggested on the literature that the presence of these solutes at the boundary are responsible for their ability to modify the texture [14], and this is the reason we are interested in studying the effects of RE elements on the grain boundary energetics. In many regards it is still an open question as to exactly how RE elements modify texture, and this paper is part of a larger computational project that aims to unravel some of these mysteries. Recently, we applied quantum mechanical calculations to try and understand the electronic origins of the rare earth effect in magnesium [19]. Specifically, we wanted to know why the RE elements displayed this behaviour, while other elements from different groups in the periodic table do not. Our calculations showed that the inclusion of rare earth elements at grain boundaries resulted in bonding states that stabilized the solid solution and increased the bonding strength between segregants and the matrix. In terms of the electronic structure of these elements, the partially occupied outer d band of RE segregants paves the way for a strong bonding between these elements and the magnesium matrix. [19]. Moreover, the local atomic packing at the boundary was observed to have impacted the electronic structure in markedly different ways. These observations shed light on why rare earth elements are potent texture modifiers during recrystallisation. However, the effect of solute concentration at the boundary has not yet been interrogated. Therefore, in the present work, we adopt a consistent computational approach to interrogate in more detail the effect of solutes and solute concentration on the grain boundary energetics. We also include in this study an additional three boundaries, and examine the differences in boundary energetics that occur when solutes adopt different locations along the grain boundary.

It is pertinent to note that much experimental, and computational effort has been devoted to characterizing microstructures arising from grains and their boundaries [20,21], the description of which includes amongst other things, their energetic [22], geometric, and topological features [21]. Nevertheless, computational studies are typically dedicated to symmetrical boundaries and this shortcoming is particularly eminent in ab initio simulations where most studies (for example [23]) restrict themselves to crystallographically simple tilt boundaries to minimise the size of the simulation to around 100 atoms. Nonetheless, the boundaries that we see experimentally are rarely simple or symmetrical. Therefore, to obtain boundaries with features that we would see experimentally, the size of the simulation cells in the present work is pushed to the largest computationally possible size in order to examine non-symmetrical grain boundaries. We examine six general boundaries consisting of tilt, twist, and irrational boundary crystallography. Two solutes are examined, Gd and Zn. Of particular interest is the grain boundary concentration. This is difficult to quantify experimentally, and therefore rarely appears in the literature. Lacking solid experimental evidence for the boundary concentrations that we might expect, we utilized atom probe tomography to examine the grain boundary concentration in a ternary Mg-Gd-Zn alloy, Figure 1. It can be seen that the boundary concentration of both Gd and Zn were found to be ~3 at% at the boundary, 6 at% total solute concentration. Therefore, in the present case our simulations were based on a notional boundary concentration of 5 at%.

2. Materials and Methods

2.1. Grain Boundary Crystallography

First principles calculations were carried out on six general boundaries in hexagonal close packed (HCP) magnesium. The crystallography of the grain boundaries was chosen to represent the major texture components observed experimentally in recrystallized magnesium alloys and are detailed in

Table 1. The crystallography of the six grain boundaries chosen for study. These are shown stereographically in Figure 2.

Grain Number		Boundary Plane and Parallel Directions	Axis and Angle of Rotation (Three Digit Indices)	Equivalent Four Digit Rotation Axis If Rational
Boundary A	Grain A1	$\left(0001\right)\langle 11\overline{2}0\rangle$	58.31° $\langle \frac{-\sqrt{3}}{2},0.5,0\rangle$	$\left[10\overline{1}0\right]$ tilt
	Grain A2	$\left(11\overline{2}2\right)\langle \overline{11}21\rangle$
Boundary B	Grain B1	$\left(10\overline{1}0\right)\langle 0001\rangle$	43.37° $\langle 0.52,-0.52,0.67\rangle$	irrational
	Grain B2	$\left(11\overline{2}2\right)\langle \overline{11}21\rangle$
Boundary C	Grain C1	$\left(10\overline{1}0\right)\langle 0001\rangle$	61.59° $\langle \frac{\sqrt{3}}{2},0.5,0\rangle$	$\left[10\overline{1}0\right]$ twist
	Grain C2	$\left(10\overline{1}0\right)\langle 1\overline{2}11\rangle$
Boundary D	Grain D1	$\left(01\overline{1}2\right)\langle 0\overline{1}11\rangle$	18.79° $\langle -1,0,0\rangle$	$\left[11\overline{2}0\right]$ tilt
	Grain D2	$\left(10\overline{1}1\right)\langle 0\overline{1}12\rangle$
Boundary E	Grain E1	$\left(0001\right)\langle 11\overline{2}0\rangle$	10.9° $\langle 0,0,1\rangle$	$\left[0001\right]$ twist
	Grain E2	$\left(0001\right)\langle 3\overline{21}0\rangle$
Boundary F	Grain F1	$\left(11\overline{2}2\right)\langle \overline{11}21\rangle$	74.8° < 1, −0.4, −0.25>	irrational
	Grain F2	$\left(10\overline{1}5\right)\langle 1\overline{2}10\rangle$

and Figure 2. Figure 2 shows that the orientations chosen to represent the different boundaries that we observed experimentally during recrystallisation of rolled magnesium. Although density functional theory (DFT) studies generally use symmetric boundaries due to the much-reduced simulation cell size required, in this work we pushed the technique to the upper limit of the cell sizes possible in order to recreate those boundaries that we know exist in real materials.

2.2. Simulation Cell Construction

The simulation cell comprises two grains and a large enough vacuum layer on top to prevent interference from the out-of-plane images due to periodic boundary conditions [24]. In order to meet the required periodic boundary condition in the grain boundary plane, without rendering the ab initio simulation unfeasible due to an overly large number of atoms in the cell, the top grain was strained in the boundary plane if required. Strains were always less than 5%.

Table 2. Details of the simulation cell size and boundary concentration levels studied.

Boundary	Cell Dimension (Å)	Number of Atoms in Simulation	Number of Atoms at GB	Solute Conc. (1 Atom)	Solute Conc. (5 Atom)	Additional Simulation
Boundary A	$5.56 \times$$6.42$ × 99.51	128	8	12.5%	62.5%	none
Boundary B	$5.21 \times$$57.78 \times$ 52.96	536	38	2.6%	13.2%	2 solute atoms = 5.3% conc.
Boundary C	$46.90 \times$$25.68 \times$ 32.10	977	140	0.7%	3.6%	7 solute atoms = 5.0% conc.
Boundary D	$15.24 \times$$35.310 \times$ 49.43	890	106	0.9%	4.7%	None
Boundary E	$16.05 \times$$27.79 \times$ 46.54	742	106	0.9%	4.7%	None
Boundary F	$30.60$ × $22.23 \times$ 43.33	846	148	0.7%	3.4%	7 solute atoms = 5.0% conc.

lists the size of each simulation cell. Additionally listed in Table 2 is the solute concentration at the boundary, measured assuming a boundary width of $\pm 0.16$ nm from the boundary. In some cases, additional simulations were made in order to obtain a data set with a constant grain boundary concentration of solute.

2.3. Calculation Details

The Vienna ab initio software package (sold commercially under the name VASP, version 6.3.0, VASP Software GmbH, Vienna, Austria) was used [25] implementing the projector augmented wave method to represent the combined potential of core electrons and nuclei [26]. The Perdew–Burke–Ernzerhof gradient approximation was implemented to represent the exchange-correlation functional [27]. A cut-off energy of 400 eV was chosen for the plane wave basis and the self-consistent electronic optimization was converged to 10⁻⁶ eV [28]. The mesh of $\mathsf{\Gamma }$-centered k-points to sample the Brillouin zone were chosen such that their density per reciprocal space is at least 50,000 Å⁻³. The atomic configuration is optimized using conjugate gradient method until mean atomic forces are less than 0.02 eV/Å⁻¹.

While the atomic representation of twin boundaries comprises a supercell containing two misoriented grains with a large enough vacuum layer on top [23,29], the general grain boundary can be considered as a general interface between two grains (G₁ and G₂) represented by two slabs. As a consequence, the simulation cell total energy is the contribution of the bulk energy of grains (${\mathrm{E}}_{\mathrm{Bulk}, \mathrm{G}1}$ and ${\mathrm{E}}_{\mathrm{Bulk},\mathrm{G}2}$), two surface energies (${\mathsf{\sigma }}_{\mathrm{G}1+}{\mathsf{\sigma }}_{\mathrm{G}2}$) and the grain boundary energy (${\mathsf{\gamma }}_{\mathrm{GB}}$) itself. Thus, the latter can be expressed as ${\mathsf{\gamma }}_{\mathrm{GB}}=$ ${\mathrm{E}}_{\mathrm{GB}}/\mathrm{S}-({\mathsf{\sigma }}_{\mathrm{G}1}+{\mathsf{\sigma }}_{\mathrm{G}2})-\left({\mathrm{E}}_{\mathrm{Bulk}, \mathrm{G}1}+{\mathrm{E}}_{\mathrm{Bulk}, \mathrm{G}2}\right)/\mathrm{S}$ and rearranging the right hand side of this equation will give [30]:

$${\mathrm{W}}_{\mathrm{sep}}=\left({\mathrm{E}}_{\mathrm{FS}}^{\mathrm{G}1}+{\mathrm{E}}_{\mathrm{FS}}^{\mathrm{G}2}-{\mathrm{E}}_{\mathrm{GB}}\right)/\mathrm{S}$$

(1)

$${\mathsf{\gamma }}_{\mathrm{GB}}={\mathsf{\sigma }}_{\mathrm{G}1}+{\mathsf{\sigma }}_{\mathrm{G}2}-{\mathrm{W}}_{\mathrm{sep}}$$

(2)

where W_SEP and S are the work of separation defined as the reversible work needed to separate the grain boundary into two free surfaces [31] and boundary area, respectively.

When solute is added to the grain boundary, the segregated grain boundary energy can be expressed as ${\mathsf{\gamma }}_{\mathrm{GB}}^{\mathrm{S}}={\mathsf{\gamma }}_{\mathrm{GB}}+{\mathrm{E}}_{\mathrm{seg}}^{\mathrm{S}}\mathsf{\Gamma }$ where ${\mathrm{E}}_{\mathrm{seg}}^{\mathrm{S}}$ and $\mathsf{\Gamma }$ are the change in segregation energy of the grain boundary and the conversion factor of segregation energy into energy per area, respectively [23].

2.4. Addition of Solutes

Two solute species were examined in this work, Zn and Gd. These elements were chosen because of the large volume of experimental data on this ternary system, for example, Figure 1 and Figure 2, and references [32,33]. Three different scenarios for solutes were considered (see Table 2 for further details):

(1)

One solute atom at five different locations along the boundary

(2)

Five solute atoms all located at the boundary

(3)

Grain boundary behaviour at a concentration of 5% (+/0.3%)

Two scenarios were considered for mixed Gd and Zn at the same boundary

(1)

1 Zn and 1 Gd atom at the boundary

(2)

2 Zn and 2 Gd atoms located at the boundary

Where five different positions at the boundary are considered, and these positions include the smallest and largest Voronoi volume cells, along with three randomly selected locations. The five locations used for the Zn and Gd simulations were the same in both cases.

3. Results

3.1. Pur Magnesium

The general grain boundaries studied herein are shown in Figure 3. They can be seen to be complex non-symmetric interfaces. We begin by examining the atomic scale differences between the boundaries, in particular how they accommodate the complex irrational interface that must form to remain contiguous. We have studied this in a previous paper using automated topology software, however it has been found that looking into the distribution of atomic size occupancy (analogous to the local lattice strain) at the interface is a more revealing methodology. Using the Voronoi analysis [23,34,35], the volume occupancy of each atom was determined. Rather than plotting the raw data, atomic volumes were converted into an equivalent spherical radius. The local lattice strain surrounding the atom was estimated by comparing the equivalent spherical radius of the atom with the radius before relaxation. The same distance either side of the boundary (less than 1.7 Angstroms) was used for all six boundaries, ensuring that the surface in contact with the vacuum in the simulation cell was not included in the analysis. The results are presented in Figure 4. Most grains showed a preference for tensile strains, indicating that in the grain boundary regions each atom had more volume to occupy compared to the bulk. Grain boundary C was the outlier, it showed a large spread in strain and the strain was more compressive than tensile.

The grain boundary energetics for pure magnesium are shown in

Table 3. Summary of grain boundary energy (γ_GB), the work of separation (W_SEP), coordination number (CN), and the width of lattice strain for the six different boundaries for simulations with only magnesium atoms included.

Boundary	ϒGB (J/m2)	WSEP (J/m2)	CN	Strain Width (%)
Boundary A	0.584	1.049	8.4	3.0
Boundary B	0.205	1.208	5.1	4.2
Boundary C	0.445	1.117	5.6	7.9
Boundary D	0.465	1.025	7.3	6.6
Boundary E	0.379	0.904	8.1	2.7
Boundary F	0.427	0.982	7.6	7.0

. Grain boundary energies range between 0.205 and 0.584 J/m², which is much larger than the energy of the commonly observed twin boundary $\left\{10\overline{1}2\right\}$ which is reported to be 0.125 J/m² [28]. The work of separation (W_SEP) for the general boundaries of pure magnesium ranges from 0.904 to 1.208 J/m², which is smaller than that of the $\left\{10\overline{1}2\right\}$ twin boundary and several other special boundaries studied in Ref [28].

3.2. Effect of Solutes

We now examine the effect of solutes on the energetics of general grain boundaries. The effect of solute location was examined using 5 different locations within the boundary region. The energy of segregation, E_seg, is a parameter which indicates the preference of a solute to be at a boundary compared to the bulk and is shown in Figure 5. The E_seg had a spread of values depending on the individual location of the solute, and the simulations with multiple solutes tended to fall somewhere in the middle of this spread.

In 64% of cases, the driving force for Gd to segregate to the boundary is larger than that of Zn. In particular, when all five locations are occupied by one type of species, ${\mathrm{E}}_{\mathrm{seg}}^{\mathrm{Gd}}$ is larger than ${\mathrm{E}}_{\mathrm{seg}}^{\mathrm{Zn}}$ in all boundaries except F. In addition, when a combination of Gd and Zn is considered (i.e., one Zn and one Gd or two Zn and two Gd), the segregation energy is always negative (i.e., solutes prefer grain boundaries over bulk) and is independent of the number of solutes. Comparing the mean value of the driving force for segregation, indicates that it is the largest for the combination of two Gd and two Zn, followed by Gd, the combination of one Gd and one Zn and finally Zn (i.e., −0.789 < −0.601 < −0.417 < −0.229, respectively).

The grain boundary energy is shown in Figure 6. When compared to the pure magnesium boundaries, the data in Figure 6 indicates that the solute location, solute concentration and solute species all have a negligible effect on the grain boundary energy. A general conclusion from looking at the grain boundary data presented here is that the boundary has an intrinsic energy, and the addition of solutes does little to disrupt this value.

One parameter which did highlight the differences that solutes imposed on the boundaries was the Work of Separation, W_SEP. This parameter has traditionally been used [29,36] to examine the cohesion of a boundary, as it indicates the work required to separate two neighbouring grains. However, in the present case we use W_SEP as a tool to identify the changes that occur when solute is located at the boundary. If we begin by comparing the W_SEP to the grain boundary energy, we can see that there is some correlation between these two parameters, and that small decreases in the grain boundary energy led to large increases in the W_SEP and vice versa, Figure 7.

The W_SEP is shown in Figure 8. There is some variation in the W_SEP for the single solute simulations, the addition of a single Zn solute could either increase or decrease W_SEP depending on its location, while the addition of a single Gd increased the W_SEP compared to pure Mg, but the magnitude varied markedly. The addition of 5 Zn solutes or 5 Gd solutes increase the W_SEP, and Gd has a larger effect than Zn. The effect of co-segregated Gd and Zn had a variable effect on W_SEP.

Due to the different size of each simulated cell, the boundary solute concentrations in each simulation are also different. Figure 8 therefore does not provide a perfect comparison between solutes and boundaries. The data is replotted in Figure 9 for five of the boundaries, all of which have ~5% solute concentration at the boundaries. Note that boundary A is not included because one solute atom provides this boundary with a concentration of 12.5%. It can be seen in Figure 9 that the different boundaries behave differently. The addition of 5%Zn has no change in W_SEP for boundaries B, D and E, while it increases W_SEP for boundaries C and F. For the case of Gd, the W_SEP is always increased by the addition of Gd solutes, but the magnitude changes markedly between boundaries. Clearly, the structure of the boundary creates a significant change in the effect of solute on W_SEP.

4. Discussion

4.1. Effct of Topology

The distribution of atoms at the boundary can best be quantified by using a pair distribution function (PDF) which was calculated at a distance of up to 0.7 of the Mg lattice parameter on either side of the grain boundary, see Figure 10. The PDF clearly indicates markedly different atomic packings and characteristics for each of the six boundaries. The most important output from this analysis is the coordination number (CN) representing the number of closest neighbours around a central atom at the boundary, Table 3. The coordination number has been used here to correlate the boundary topology with the calculated energetics of the boundary (Figure 11). It can be seen that there is a slight increase in W_SEP for lower values of coordination number, where lower CN values correlate with more disorder at the boundary.

It was seen in Figure 6 and Figure 8, respectively, that the effect of solute on GB energy was negligible but was significant for W_SEP. We can see from Figure 11 that the addition of Zn to the boundary increased the W_SEP value, but this did not correlate with CN. However, Gd shows a tendency to increase the value of W_SEP more for the more disordered boundaries with lower coordination numbers. It must also be concluded from this data that the effect of solutes on the boundary is not easily defined and shows significant variability across many energetic parameters examined here, such as the ones shown in Figure 5, Figure 6 and Figure 8.

The topology of the boundary also had a significant effect on the electronic structure [37], which can clearly be seen in the pDOS of the profile of the d-orbital of Gd in bulk Mg, and in the boundaries A, B, and C (with CNs of 12, 8.4, 5.1, and 5.6, respectively) as depicted in Figure 12. Indeed, the least smooth profile corresponds to the boundary B with the lowest CN, and the most similar one to the solute in the bulk Mg corresponds to the boundary A with largest CN.

4.2. Effect of Solute on GB Energetics

Figure 13 shows the W_SEP data from all simulations for all boundaries, plotted as a function of grain boundary concentration. Note that the concentration scale in Figure 13 (a) is much larger than the other boundaries due to the relatively smaller size of that simulation cell. It can be seen that there is a generalized trend towards increasing W_SEP with increasing solute concentration. This can be understood by considering the solute bonding behaviours. Previous work quantified the strength of the bond between magnesium and the solutes Gd and Zn using the crystal orbital Hamiltonian population method [19] where it was demonstrated that Gd had a stronger bond to Mg than Zn did, but the bonding of both solutes with the Mg matrix was stronger than the bonds between Mg matrix. With increasing concentration at the boundary there will be more solutes, and these provide more bonds, leading to the general trend of increasing W_SEP with increasing solute concentration. This also explains why Gd tends to have a larger W_SEP than Zn, Gd has been found to bond more strongly to the grain boundary than zinc. In addition, worth mentioning is the rate of increase in W_SEP with concentration. Boundaries A and D show a much lower increase in W_SEP per atomic percent increase in solute concentration. These boundaries also show high values of CN and show narrow lattice strain distributions (Figure 4), and it may be the case that the W_SEP is more sensitive to solute in disordered boundaries, resulting in showing a steeper increase in W_SEP with increasing solute concentration. This is consistent with the data shown in Figure 10.

5. Conclusions

Density functional theory was used to examine the energetics, topology, electronic structure and the bonding behaviour of Gd and Zn solutes in magnesium at six different general grain boundaries. The premise of the work was that the presence of these solutes at the boundary are responsible for texture development [14]. The boundary crystallography was chosen from experimental data, and comprised two twist, two tilt, and two irrational boundaries. In order to simulate these general grain boundaries, as opposed to idealized symmetrical tilt boundaries, very large simulation cell sizes were required. The resulting grain boundaries were interrogated, and the solute species (Gd and Zn) were placed in multiple locations to investigate their effect on the boundary. The following conclusions have been made:

• The grain boundaries were found to have an intrinsic grain boundary energy, and this energy was not markedly affected by the solute concentration or chemistry at the boundary.
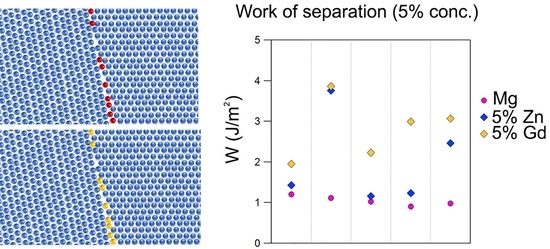
• In contrast with grain boundary energy, the work of separation (W_SEP) was very sensitive to grain boundary chemistry. This parameter was therefore used to interrogate the effect of solute on grain boundary behaviour. It was found that for a boundary solute concentration of 5 at%, the effect of Zn and Gd on the W_SEP was markedly different for the different boundaries. This is indicative that the two solutes will have a different effect on different boundary types.
• The topology of the grain boundary was correlated with the boundary energetics using the coordination number. For pure magnesium, the work of separation was found to correlate with coordination number, with more disordered boundaries of low CN showing higher values of W_SEP. The effect of solute was not directly correlated with the CN, but there was a general trend for Gd to increase the W_SEP more in those boundaries of low CN (high disorder).
• The W_SEP was found to increase with increasing boundary solute concentration, with the rate of change being markedly different between the different boundaries. The increase in W_SEP with solute concentration was typically higher for Gd compared to Zn.
• No correlation between the boundary behaviour and crystallography could be found, apart from the over-riding conclusion that all six boundaries showed different behaviours, and the effect of solute on their W_SEP were unique.