Dust-Ion-Acoustic Rogue Waves in a Dusty Plasma Having Super-Thermal Electrons
Abstract
:1. Introduction
2. Governing Equations
3. Derivation of the NLSE
4. Modulational Instability and Rogue Waves
5. Results and Discussion
6. Conclusions
- Fast and slow DIA modes have been observed.
- Both modulationally stable (i.e., ) and unstable (i.e., ) parametric regimes of the DIAWs can exist for both fast and slow modes.
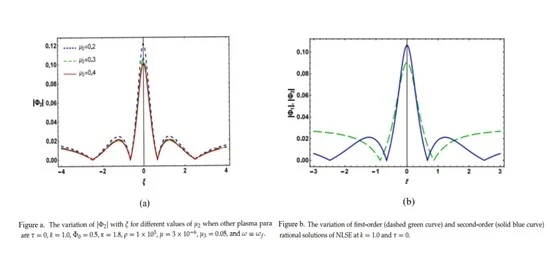
- The amplitude of the first and second-order DIARWs decreases (increases) with ion (electron) temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eslami, P.; Mottaghizadeh, M.; Pakzad, H.R. Nonplanar dust-ion acoustic solitary waves in warm plasma with superthermal electrons. IEEE Trans. Plasma Sci. 2013, 41, 3589. [Google Scholar] [CrossRef]
- Shahmansouri, M.; Tribeche, M. Dust acoustic localized structures in an electron depleted dusty plasma with two-suprathermal ion-temperature. Astrophys. Space Sci. 2012, 342, 87. [Google Scholar] [CrossRef]
- Saini, N.S.; Singh, K. Head-on collision of two dust ion acoustic solitary waves in a weakly relativistic multicomponent superthermal plasma. Phys. Plasmas 2016, 23, 103701. [Google Scholar] [CrossRef]
- Shukla, P.K.; Mamun, A.A. Introduction to Dusty Plasma Physics; Institute of Physics: Bristol, UK, 2002. [Google Scholar]
- Zaman, D.M.S.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Dust-acoustic rogue waves in opposite polarity dusty plasma featuring nonextensive statistics. High Temp. 2020, 58, 789. [Google Scholar] [CrossRef]
- Boufendi, L.; Bouchoule, A. Industrial developments of scientific insights in dusty plasmas. Plasma Sources Sci. Technol. 2002, 11, 211. [Google Scholar] [CrossRef]
- Gill, T.S.; Bains, A.S.; Bedi, C. Modulational instability of dust acoustic solitons in multicomponent plasma with kappa-distributed electrons and ions. Phys. Plasmas 2010, 17, 013701. [Google Scholar] [CrossRef]
- Alinejad, H.; Mahdavi, M.; Shahmansouri, M. Modulational instability of ion–acoustic waves in a plasma with two-temperature kappa-distributed electrons. Astrophys. Space Sci. 2014, 352, 571. [Google Scholar] [CrossRef]
- Gharaee, H.; Afghah, S.; Abbasi, H. Modulational instability of ion-acoustic waves in plasmas with superthermal electrons. Phys. Plasmas 2011, 18, 032116. [Google Scholar] [CrossRef]
- Ferdousi, M.; Sultana, S.; Hossen, M.M.; Miah, M.R.; Mamun, A.A. Dust-acoustic shock excitations in κ-nonthermal electron depleted dusty plasmas. Eur. Phys. J. D 2017, 71, 102. [Google Scholar] [CrossRef]
- Rahman, M.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-acoustic rogue waves in an electron-positron-ion-dust plasma medium. Galaxies 2021, 9, 31. [Google Scholar] [CrossRef]
- Jahan, S.; Haque, M.N.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Ion–acoustic rogue waves in double pair plasma having non-extensive particles. Universe 2021, 7, 63. [Google Scholar] [CrossRef]
- Sikta, J.; Chowdhury, N.A.; Mannan, A.; Sultana, S.; Mamun, A.A. Electrostatic dust-acoustic rogue waves in an electron depleted dusty plasma. Plasma 2021, 4, 230–238. [Google Scholar] [CrossRef]
- Maksimovic, M.; Gary, S.P.; Skoug, R.M. Solar wind electron suprathermal strength and temperature gradients: Ulysses observations. J. Geophys. Res. 2000, 105, 18337. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M. Kappa distributions: Theory and applications in space plasmas. Sol. Phys. 2010, 267, 153. [Google Scholar] [CrossRef] [Green Version]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839. [Google Scholar] [CrossRef]
- Amin, M.R.; Morfill, G.E.; Shukla, P.K. Modulational instability of dust-acoustic and dust-ion-acoustic waves. Phys. Rev. E 1998, 58, 6517. [Google Scholar] [CrossRef]
- Jukui, X.; He, L. Modulational instability of cylindrical and spherical dust ion–acoustic waves. Phys. Plasmas 2003, 10, 339. [Google Scholar] [CrossRef]
- Saini, N.S.; Kourakis, I. Dust-acoustic wave modulation in the presence of superthermal ions. Phys. Plasmas 2008, 15, 123701. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L. Three-dimensional dust-ion-acoustic rogue waves in a magnetized dusty pair-ion plasma with nonthermal nonextensive electrons and opposite polarity dust grainsa. Phys. Plasmas 2014, 21, 082303. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Sun, A. Nonlinear ion–acoustic structures in a nonextensive electron–positron–ion–dust plasma: Modulational instability and rogue waves. Ann. Phys. 2012, 332, 38. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Mei, L.; Shi, W. Rogue wave triplets in an ion-beam dusty plasma with superthermal electrons and negative ions. Phys. Lett. A 2013, 377, 2118. [Google Scholar] [CrossRef]
- Almutalk, S.A.; El-Tantawy, S.A.; El-Awady, E.I.; El-Labany, S.K. On the numerical solution of nonplanar dust-acoustic super rogue waves in a strongly coupled dusty plasma. Phys. Lett. A 2019, 16, 1937. [Google Scholar] [CrossRef]
- Denra, R.; Paul, S.; Ghosh, U.; Sarkar, S. Nonlinear dust-acoustic wave propagation in a Lorentzian dusty plasma in presence of negative ions. J. Plasma Phys. 2018, 84, 5. [Google Scholar] [CrossRef]
- Dubinov, A.E.; Kitayev, I.N. Nonlinear periodic backward dust acoustic waves. Planet. Space Sci. 2021, 195, 105142. [Google Scholar] [CrossRef]
- El-Labany, S.K.; El-Taibany, W.F.; El-Tantawy, A.A.; Zedan, N.A. Effects of double spectral electron distribution and polarization force on dust acoustic waves in a negative dusty plasma. Contrib. Plasma Phys. 2020, 60, e202000049. [Google Scholar] [CrossRef]
- El-Taibany, W.F.; El-Labany, S.K.; Behery, E.E.; Abdelghany, A.M. Nonlinear dust acoustic waves in a self-gravitating and opposite-polarity complex plasma medium. Eur. Phys. J. Plus 2019, 134, 457. [Google Scholar] [CrossRef]
- Chahal, B.S.; Singh, M.; Saini, N.S. Dust ion acoustic freak waves in a plasma with two temperature electrons featuring Tsallis distribution. Phys. A 2018, 491, 935. [Google Scholar] [CrossRef]
- El-Labany, S.K.; El-Shewy, E.K.; Abd El-Razek, H.N.; El-Rahman, A.A. Dust-Ion Acoustic Freak Wave Propagation in a Nonthermal Mesospheric Dusty Plasma. Plasma Phys. Rep. 2017, 43, 576. [Google Scholar] [CrossRef]
- Mandi, L.; Mondal, K.K.; Chatterjee, P. Analytical solitary wave solution of the dust ion acoustic waves for the damped forced modified Korteweg-de Vries equation in q-nonextensive plasmas. Eur. Phys. J. Spec. Top. 2019, 228, 2753. [Google Scholar] [CrossRef]
- Paul, A.; Bandyopadhyay, A.; Das, K.P. Dust ion acoustic solitary structures at the acoustic speed in the presence of nonthermal electrons and isothermal positrons. Plasma Phys. Rep. 2019, 45, 466. [Google Scholar] [CrossRef] [Green Version]
- Sinha, A.; Sahu, B. dust-ion-acoustic waves in unmagnetized 4-component plasma. Adv. Space Res. 2021, 67, 1244. [Google Scholar] [CrossRef]
- Farooq, M.; Ahmad, M. Dust ion acoustic waves in four component magnetized dusty plasma with effect of slow rotation and superthermal electrons. Phys. Plasmas 2017, 24, 123707. [Google Scholar] [CrossRef]
- Das, R.; Karmakar, K. Fast and slow modes on dust ion acoustic solitary waves in a warm plasma. Int. J. Sci. Res. 2013, 3, 63. [Google Scholar]
- Mowafy, A.E. Propagation of the dust ion acoustic waves in inhomogeneous warm dusty plasma. Afr. Rev. Phys. 2012, 7, 0032. [Google Scholar]
- Heera, N.M.; Akter, J.; Tamanna, N.K.; Chowdhury, N.A.; Rajib, T.I.; Sultana, S.; Mamun, A.A. Ion–acoustic shock waves in a magnetized plasma featuring super-thermal distribution. AIP Adv. 2021, 11, 055117. [Google Scholar] [CrossRef]
- Banik, S.; Shikha, R.K.; Noman, A.A.; Chowdhury, N.A.; Mannan, A.; Roy, T.S.; Mamun, A.A. First and second-order dust-ion-acoustic rogue waves in non-thermal plasma. Eur. Phys. J. D 2021, 75, 43. [Google Scholar] [CrossRef]
- Shikha, R.K.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Electrostatic dust-acoustic envelope solitons in an electron-depleted plasma. Contrib. Plasma Phys. 2021, 61, e202000117. [Google Scholar] [CrossRef]
- Khondaker, S.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Rogue waves in multi-pair plasma medium. Contrib. Plasma Phys. 2019, 59, e201800125. [Google Scholar] [CrossRef] [Green Version]
- Dubinov, A.E. On a widespread inaccuracy in defining the Mach number of solitons in a plasma. Plasma Phys. Rep. 2009, 35, 991. [Google Scholar] [CrossRef]
- Saberian, E.; Esfandyari-Kalejahi, A.; Afsari-Ghazi, M. Nonlinear dust-acoustic structures in space plasmas with superthermal electrons, positrons, and ions. Plasma Phys. Rep. 2017, 43, 83. [Google Scholar] [CrossRef]
- Shukla, P.K.; Silin, V. Dust ion–acoustic wave. Phys. Scr. 1992, 45, 508. [Google Scholar] [CrossRef]
- Barkan, A.; Angelo, N.D.; Merlino, R.L. Experiments on ion–acoustic waves in dusty plasmas. Planet. Space Sci. 1996, 44, 239. [Google Scholar] [CrossRef]
- Kourakis, I.; Shukla, P.K. Modulational instability and localized excitations of dust-ion acoustic waves. Phys. Plasmas 2003, 10, 3459. [Google Scholar] [CrossRef] [Green Version]
- Kourakis, I.; Shukla, P.K. Exact theory for localized envelope modulated electrostatic wavepackets in space and dusty plasmas. Nonlinear Proc. Geophys. 2005, 12, 407. [Google Scholar] [CrossRef]
- Fedele, R. Envelope solitons versus solitons. Phys. Scr. 2002, 65, 502. [Google Scholar] [CrossRef]
- Noman, A.A.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-acoustic envelope solitons in super-thermal plasmas. Contrib. Plasma Phys. 2019, 59, e201900023. [Google Scholar] [CrossRef] [Green Version]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef] [Green Version]
- Ankiewicz, A.; Devine, N.; Akhmediev, N. Are rogue waves robust against perturbations? Phys. Lett. A 2009, 373, 3997. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.; Konopka, U.; Khrapak, S.A.; Morfill, G.E.; Sen, A. Effect of polarization force on the propagation of dust acoustic solitary waves. New J. Phys. 2010, 12, 073002. [Google Scholar] [CrossRef]
- Zadorozhny, A.M. Effects of charged dust on mesospheric electrical structure. Adv. Space Res. 2001, 28, 1095. [Google Scholar] [CrossRef]
- Wang, Y.L.; Guo, X.Y.; Li, Q.S. Nonlinear dust acoustic waves in strongly coupled dusty plasmas with charged dust particles. Commun. Theor. Phys. 2016, 65, 247. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.; Prasad, G.; Sen, A.; Kaw, P.K. Experimental study of nonlinear dust acoustic solitary waves in a dusty plasma. Phys. Rev. Lett. 2012, 101, 065006. [Google Scholar] [CrossRef] [Green Version]
- Shalini; Saini, N.S. Dust ion acoustic rogue waves in superthermal warm ion plasma. J. Plasma Phys. 2015, 81, 905810316. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noman, A.A.; Islam, M.K.; Hassan, M.; Banik, S.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-Ion-Acoustic Rogue Waves in a Dusty Plasma Having Super-Thermal Electrons. Gases 2021, 1, 106-116. https://doi.org/10.3390/gases1020009
Noman AA, Islam MK, Hassan M, Banik S, Chowdhury NA, Mannan A, Mamun AA. Dust-Ion-Acoustic Rogue Waves in a Dusty Plasma Having Super-Thermal Electrons. Gases. 2021; 1(2):106-116. https://doi.org/10.3390/gases1020009
Chicago/Turabian StyleNoman, Akib Al, Md Khairul Islam, Mehedi Hassan, Subrata Banik, Nure Alam Chowdhury, Abdul Mannan, and A. A. Mamun. 2021. "Dust-Ion-Acoustic Rogue Waves in a Dusty Plasma Having Super-Thermal Electrons" Gases 1, no. 2: 106-116. https://doi.org/10.3390/gases1020009