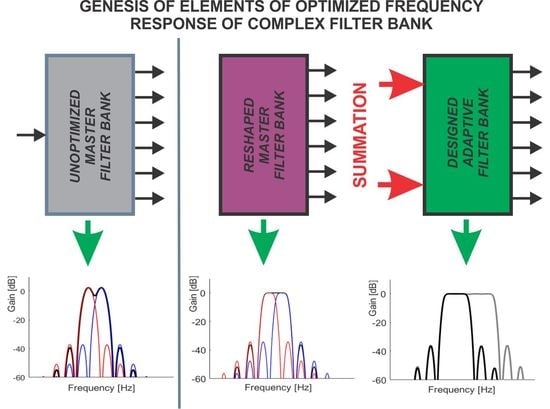
IIR Cascaded-Resonator-Based Complex Filter Banks

Abstract

The use of a filter bank of IIR filters for the spectral decomposition and analysis of signals has been popular for many years. As such, a new filter-bank resonator-based structure, representing an extremely hardware-efficient structure, has received a good deal of attention. Recently, multiple-resonator (MR)-based and general cascaded-resonator (CR)-based filters have been proposed. In comparison to single-resonator-based analyzers, analyzers with a higher multiplicity of resonators in the cascade provide lower side lobes and a higher attenuation in stopbands. In previous works, it was shown that the CR-based filter bank with infinite impulse response (IIR) filters, which is numerically more efficient than one with finite impulse response (FIR) filters, is suitable for dynamic harmonic analysis. This paper uses the same approach to design complex digital filter banks. In the previous case, the optimization task referred to the frequency responses of harmonic filters. In this work, the harmonic filters of the mother filter bank are reshaped so that the frequency response of the sum (or difference, depending on the parity of the number of resonators in the cascade) of two adjacent harmonic filters is optimized. This way, an online adaptive filter base can be obtained. The bandwidth of the filters in the designed filter bank can be simply changed online by adding or omitting the output signals of the corresponding harmonics of the mother filter.

1. Introduction

A huge variety of engineering applications, such as speech analysis, bandwidth compression, radar and sonar processing, spectral parameterization of signals, adaptive line enhancement, tracking of periodic signals, sub-band coding, and frequency-domain adaptive noise-cancellation, have caused much attention to be paid to the study of filter banks and corresponding analysis/synthesis system designs. In signal processing, a digital filter bank is an array of digital bandpass filters with either a common input or a common output. This means that a filter bank can be an analysis filter bank or a synthesis filter bank [1].

The understanding of the systems is often simplified, and performances in signal processing are improved by considering the signals and/or system transfer functions as complex types. For example, a new concept of digital equalizers is based on the processing of so-called analytic signals, i.e., signals consisting only of positive frequencies, with digital filters with complex coefficients as the main building blocks of the equalizer. The transfer functions of these filters are complex functions, and the input signals are separated into real and imaginary parts, even in the case of a real input signal. It is true that this approach requires more arithmetical operations than a classical real approach. However, it has been shown that the proposed equalizer offers some new features, which make it very attractive for various applications [2]. Although digital filters with complex coefficients have been known for a long time and have many advantages, in the last few decades, work on the realization of these filters has become much more current [3,4,5,6,7,8]. Complex filtering is very popular in telecommunications, where the complex representation of signals allows the simple realization and interpretation of complex tasks such as sampling, quantization, or modulation. Additionally, speech processing and adaptive filtering cannot be imagined without the use of digital filters with complex coefficients. For example, complex digital signal processing can increase speech understanding of users of bone-anchored hearing aids when the benefit is most significant for speech understanding in noise [6].

Resonator-based filter banks, based on the structure of parallel resonators with common feedback, are an example of complex filter banks [9,10,11]. Multiple-resonator (MR)-based filters [12,13] and their more general version, cascaded-resonator (CR)-based filters [14,15,16], have been proposed for usage in the spectrum analysis of dynamic signals. In comparison to single-resonator-based analyzers, analyzers with a higher multiplicity of resonators provide lower side lobes. In [16], infinite-impulse-response (IIR)-type CR-based filter banks were used as a computationally more efficient solution, rather than the finite-impulse-response (FIR)-type. Even more, through simultaneous optimization of the frequency responses of the whole harmonic bank, the same shapes of all harmonic frequency responses were assured, thanks to symmetrical pole placement.

In this paper, the approach used in [16], with certain modifications, is used to design online adaptive filter banks. Bandpass filters of arbitrary width can be obtained by connecting filters of the appropriate number of adjacent harmonics of the primary filter bank. Considering the high attenuation in the stopbands of the filter of the primary filter bank, especially in the case of resonator structures with a larger number of resonators in the cascade, it is sufficient to reshape the frequency responses of the harmonic filters in the primary bank so as to optimize the frequency characteristic of the sum (or difference, depending on the parity of the number of resonators in the cascade) of only two adjacent harmonics, in the range between their central frequencies, since the influence of the others can be neglected. The sidelobes of this group of two harmonics can also be limited or optimized during optimization.

An important advantage of this approach is that the different bandwidths of the output filters can be simply adjusted online by adding the required number of the adjacent channels to the basic filter bank, and can be easily performed by adding and/or omitting certain output signals from the primary filter bank. In addition, transition bands of the frequency responses can be decreased by increasing the number of resonator cascades. The drawback of this approach is the considerable computational complexity which could be a possible problem in low-price and low-power applications.

2. Design Method

The block diagram of the $K$-type CR-based harmonic analyzer is shown in Figure 1. The structure includes $\left(K+1\right)\left(2M+2\right)$ resonators with poles $\left\{z_{m,k},m=-M,\dots ,0,\dots ,M+1,k=0,1,\dots ,K\right\}$ placed in the $2M+2$ cascades, each with $K+1$ cascaded complex poles on the unit circle located around the related harmonic frequency. Each resonator has complex gains $g_{m,k}$. The following closed-loop transfer function corresponds to the harmonic $m$ [16]:

$$H_m^{AB}\left(z\right)=\frac{V_m\left(z\right)}{V\left(z\right)}=g_{m,0}^{\prime }\frac{{z^{-1}P}_m\left(z\right)B\left(z\right)}{A\left(z\right)}=H_m\left(z\right)\frac{B\left(z\right)}{A\left(z\right)},$$

(1)

where $z=e^{j\omega }$, $\omega =2\pi f/f_S$, $f_S$ is the sampling rate, and $f_1$ is the fundamental frequency.

$$P_m\left(z\right)=\prod _{\begin{array}{c}n=-M\\ n\ne m\end{array}}^{M+1}\prod _{i=0}^K\left(1-z_{n,i}{z}^{-1}\right),{ g}_{m,k}^{\prime }=\prod _{i=k}^K{g}_{m,i},$$

(2)

$$H_m\left(z\right)=g_{m,0}^{\prime }{z^{-1}P}_m\left(z\right),$$

$$B\left(z\right)=b_0+b_1{z}^{-1}+\cdots +b_{N_B-1}{z}^{-\left(N_B-1\right)}+b_{N_B}{z}^{-N_B},$$

$$A\left(z\right)=1+a_1{z}^{-1}+\cdots +a_{N_A-1}{z}^{-\left(N_A-1\right)}+a_{N_A}{z}^{-N_A}.$$

It should be noted that all poles of the resonators are transformed into zeros of the transfer functions $H_m\left(z\right)$ by the common feedback loop, except the poles originating from channel $m$, which are automatically cancelled by their poles–generators.

Figure 2 shows the frequency responses of $H_1\left(z\right)=g_{\mathrm{1,0}}^{\prime }{z^{-1}P}_1\left(z\right)$ belonging to the fundamental component of the resonator multiplicity order from one to six $(K=\mathrm{0,1},\dots ,5$) with the ordinate scale in decibels. It should be noted that case $K=0$ corresponds to the classic DFT estimator, while case $K>0$ corresponds to the discrete Taylor–Fourier transform (DTFT), which was recently proposed as a DFT extension [17]. It is obvious that with an increase in the number of resonators in the cascade, the suppression in the stopband increases and the side lobes decrease. However, with an increase in $K$, the filter order and the response time, as well as the numerical complexity, increase.

The problem of frequency deviation can be solved in two ways. The first way is an adaptive estimator based on actual frequency feedback. This approach is sensitive to the system stability issue due to internal delays. Instead of that, in [18], an external module was used to estimate the fundamental frequency, on the basis of which the adaptation of the resonator poles and gain coefficients was carried out.

The compensation polynomial $B\left(z\right)$ is the only real extension to the basic CR structure that increases the computational burden, while the characteristic polynomial $A\left(z\right)$ does not increase numerical operation and only influences the gains’ calculation. $A\left(z\right)$ is of the order $N_A=\left(K+1\right)\left(2M+2\right)$. It should be mentioned that because of symmetry, order $N_B$ of the polynomial $B\left(z\right)$ must be a product of the number of harmonic cascades $2M+2$.

2.1. Problem Statement

The important feature of the mother bank $\left\{H_m\left(z\right),m=-M,\dots ,0,\dots ,M+1\right\}$ is that the phase difference of adjacent filters is $\left(K+1\right)\pi$ for the band between their center frequencies (i.e., 0 for an odd $K$ and $\pi$ for an even $K$) and zero elsewhere. The idea is to superpose the frequency responses of a certain number of adjacent harmonics (with a sign “+” in the case of odd $K$, and an alternating “−” and “+” signs in the even $K$ case). Figure 3 shows the frequency responses of sums of two, three, and five adjacent harmonic channels for $K=2$, $f_S=4 \mathrm{k}\mathrm{H}\mathrm{z}$ and $f_1=125 \mathrm{H}\mathrm{z}$. It is notable that the level of sidelobes is not increased, but the ripple in the passband is present. In order to reduce the ripple, it is necessary to design the polynomials $A\left(z\right)\ne 1$ and/or $B\left(z\right)$.

The virtual unique combined transfer function $H\left(z\right)$ is formed from segments of the transfer functions corresponding to the frequency bands between two adjacent harmonic frequencies. Every two adjacent filters of harmonics $m$ and $m+1$ participate together in the band $\left(m{f}_1,\left(m+1\right)f_1\right)$ with their sum:

$$H\left(z\right)=H_m\left(z\right)\mp H_{m+1}\left(z\right)=z^{-1}\left[g_{m,0}^0{P}_m\left(z\right)\mp {g_{m+\mathrm{1,0}}^{0}P}_{m+1}\left(z\right)\right],$$

(3)

for $f\in \left(m{f}_1,\left(m+1\right)f_1\right)$, $m=-M,\dots ,0,\dots ,M+1$, where gain coefficients $g_{m,0}^0=z_m/P_m\left(z_m\right)$,$m=-M,\dots ,0,\dots ,M+1$, provide unity gains in the frequencies $m{f}_1$ and $\left(m+1\right)f_1$.

A sign “−” is used for an even $K$ ($K=0,2,4,\dots$), and “+” is used for an odd $K$ ($K=1,3,5,\dots$). It should be noted that in cases when the width of the output filter is greater than two harmonic bands, there is the influence of harmonics of the order less than $m$ and greater than $m+1$ in the band $\left(m{f}_1,\left(m+1\right)f_1\right)$, but it can be neglected, especially for a larger $K$. Note that for $m=M+1$, $f\in \left(-\left(M+1\right)f_1,-M{f}_1\right)$ and $H\left(z\right)=H_{M+1}\left(z\right)\mp H_{-M}\left(z\right)$.

The group delay (in samples) and phase response of $H\left(z\right)$ are ${\tau }_H=\left(K+1\right)\left(2M+2\right)/2$ and $\mathrm{a}\mathrm{r}\mathrm{g}\left(H\left(z\right)\right)={\tau }_H\left(\omega -m{\omega }_1\right)$, respectively.

The corresponding desired linear phase transfer function is defined as follows

$$H^d\left(z\right)=e^{-j\left[{\tau }_H\left(\omega -m{\omega }_1\right)+{\tau }_B\omega \right]},$$

(4)

$$\mathrm{for} f\in \left(m{f}_1,\left(m+1\right)f_1\right),m=-M, \dots ,0, \dots ,M+1,$$

where a desired group delay is increased by the settled value of ${\tau }_B$ caused by the presence of $B\left(z\right)/A\left(z\right)$, which is in the range of $\left(0.5÷1\right)N_B$.

We seek to find a causal stable rational function $H^{AB}\left(z\right)=H\left(z\right)B\left(z\right)/A\left(z\right)$ that best approximates $H^d\left(z\right)$ in the defined sense. Since $H\left(z\right)$ is defined by poles $\left\{z_{m,k},m=-M,\dots ,0,\dots ,M+1,k=0,1,\dots ,K\right\}$, it is necessary to determine the coefficients of the filter $B\left(z\right)/A\left(z\right)$ and after that, for the determined $A\left(z\right)$, gains $g_{m,k}^{\prime }$, i.e., $g_{m,k}$.

In [19], the following definition of the approximation error in the angular frequency ${\omega }_i$, in the $k$th time instant, that allows an iterative scheme is used:

$$\left|E_i^{\left(k\right)}\left(\mathit{x}\right)\right|=\frac{W\left(z_i\right)\left|H\left(z_i\right)B\left(z_i\right)-A^{\left(k\right)}\left(z_i\right)H^d\left(z_i\right)\right|}{\left|A^{\left(k-1\right)}\left(z_i\right)\right|},$$

(5)

where $A^{\left(k\right)}\left(z\right)$ and $A^{\left(k-1\right)}\left(z\right)$ are the polynomial $A\left(z\right)$ in the iterations $k$ and $k-1$, respectively, and $W\left(z\right)$ is the chosen weighing function. The above equality can be expressed as

$$\left|E_i^{\left(k\right)}\left(\mathit{x}\right)\right|=\frac{W\left(z_i\right)\left|\left[{\left.{H\left(z_i\right)\mathit{q}}_{\mathit{B}}\right|}_{z=z_i},{\left.-H^d\left(z_i\right){\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right]\mathit{x}-H^d\left(z_i\right)\right|}{\left|A^{\left(k-1\right)}\left(z_i\right)\right|}=\left|{\mathit{h}}_{\mathit{i}}\mathit{x}-g_{\mathit{i}}\right|,$$

(6)

where

$\mathit{x}={\left[\begin{array}{cc}{{\mathit{x}}_{\mathit{B}}}^T& {{\mathit{x}}_{\mathit{A}}}^T\end{array}\right]}^T$,

${\mathit{x}}_{\mathit{B}}={\left[\begin{array}{ccc}{b}_0& b_1& \cdots \end{array}\begin{array}{ccc}& b_{N_B-1}& b_{N_B}\end{array}\right]}^T$,

${\mathit{x}}_{\mathit{A}}={\left[\begin{array}{cc}{a}_1& a_2\end{array}\cdots \begin{array}{cc}{a}_{N_A-1}& a_{N_A}\end{array}\right]}^T$,

${\mathit{q}}_{\mathit{B}}=\left[\begin{array}{ccc}1& z^{-1}& z^{-2}\end{array}\begin{array}{ccc}\cdots & z^{-\left(N_B-1\right)}& z^{-N_B}\end{array}\right]$,

${\mathit{q}}_{\mathit{A}}=\left[\begin{array}{cc}{z}^{-1}& z^{-2}\end{array}\begin{array}{ccc}\cdots & z^{-\left(N_A-1\right)}& z^{-N_A}\end{array}\right]$,

$${\mathit{h}}_i=\frac{W\left(z_i\right)\left[{\left.{H\left(z_i\right)\mathit{q}}_{\mathit{B}}\right|}_{z=z_i},{\left.-H^d\left(z_i\right){\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right]}{\left|A^{\left(k-1\right)}\left(z_i\right)\right|},$$

$$g_i=\frac{W\left(z_i\right)H^d\left(z_i\right)}{\left|A^{\left(k-1\right)}\left(z_i\right)\right|}.$$

It can be noticed that the $\left|E_i^{\left(k\right)}\left(x\right)\right|$ and the constraint (8) are nonlinear. They can be linearized using convenient approximation [20,21,22]. This means the optimization problem can be solved using the constrained linear least-squares (CLLS) optimization technique, as in [20,21], or linear programming (LP) in the case of minimax optimization, as in [16,19,22].

2.2. Design (Optimization) Approach 1—Linear Least-Squares Minimization

An objective is to find a minimum of the sum of squares of absolute values of $\mathit{h}\mathit{x}-g$ in the assembly of the $N_F$ selected frequencies subject to the vector $\mathit{x}$

$$\underset{\mathit{x}}{\min }{\sum }_{i=1}^{N_F}{\left|{\mathit{h}}_i\mathit{x}-g_i\right|}^2.$$

(7)

If we apply the equality

$${\left|{\mathit{h}}_i\mathit{x}-g_i\right|}^2={\mathrm{R}\mathrm{e}}^2\left\{{\mathit{h}}_i\mathit{x}-g_i\right\}+{\mathrm{I}\mathrm{m}}^2\left\{{\mathit{h}}_i\mathit{x}-g_i\right\}={‖{\mathit{C}}_i\mathit{x}-{\mathit{d}}_i‖}_2^2,$$

(8)

where ${\mathit{C}}_i=\left[\begin{array}{c}\mathrm{Re}\left\{{\mathit{h}}_i\right\}\\ \mathrm{Im}\left\{{\mathit{h}}_i\right\}\end{array}\right]$, ${\mathit{d}}_i=\left[\begin{array}{c}\mathrm{Re}\left\{g_i\right\}\\ \mathrm{Im}\left\{g_i\right\}\end{array}\right]$, the expression (7) can be written in a matrix form:

$$\underset{\mathit{x}}{\min }{‖\mathit{C}\mathit{x}-\mathit{d}‖}_2^2,$$

(9)

where

$\mathit{C}=\left[\begin{array}{c}{\mathit{C}}_1\\ {\mathit{C}}_2\\ ⋮\\ {\mathit{C}}_{N_F}\end{array}\right]$, $\mathit{d}=\left[\begin{array}{c}{\mathit{d}}_1\\ {\mathit{d}}_2\\ ⋮\\ {\mathit{d}}_{N_F}\end{array}\right]$.

2.3. Design (Optimization) Approach 2—Minimax Optimization

It is well known that to find $\mathit{x}$ to minimize the maximum error $\underset{\mathit{i}}{\max }\left|E_i^{\left(k\right)}\left(\mathit{x}\right)\right|$ is equivalent to the following optimization problem:

$$\mathrm{minimize}\hspace{1em}\delta$$

(10)

$$\mathrm{subject}\hspace{0.33em}\mathrm{to}\left|E_i^{\left(k\right)}\left(\mathit{x}\right)\right|\le \delta , i=\mathrm{1,2},\cdots ,N_F,$$

where $N_F$ is the total number of sampling points in the design bands (0 ≤ ω ≤ π).

The vector of compensator coefficient $\mathit{x}$ is extended with $\delta$ so that a vector of unknowns is:

$${\mathit{x}}^{\delta }=\left[\begin{array}{c}\mathit{x}\\ \delta \end{array}\right].$$

(11)

It can be noticed that the constraints in (10) are nonlinear. They can be linearized using convenient approximation [16,20,21]. This allows the problem to be solved using linear programming (LP).

It is valid that

$$\left|E\left(z_i\right)\right|=\left|E\left(z_i\right)\right|\left({\mathrm{c}\mathrm{o}\mathrm{s}}^2{\alpha }_i+{\mathrm{s}\mathrm{i}\mathrm{n}}^2{\alpha }_i\right)=\mathrm{R}\mathrm{e}\left\{E\left(z_i\right)\right\}\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_i+\mathrm{I}\mathrm{m}\left\{E\left(z_i\right)\right\}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_i,$$

(12)

where ${\alpha }_i=\mathrm{a}\mathrm{r}\mathrm{g}\left\{E\left(z_i\right)\right\}$.

Since ${\alpha }_i$ is not known a priori, the nonlinear constraints in (10) can be approximated by the system of linear constraints:

$$\mathrm{R}\mathrm{e}\left\{E\left(z_i\right)\right\}\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_{i,j}+\mathrm{I}\mathrm{m}\left\{E\left(z_i\right)\right\}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_{i,j}\le \delta ,$$

(13)

where $i=\mathrm{1,2},\cdots ,N_F$ and $j=\mathrm{1,2},\cdots ,L$. The number of constraints $L$ is chosen depending on the requested tolerance. An equidistant placement of the angles is the most convenient, i.e., ${\alpha }_{i,j}={\alpha }_{i,0}+\left(j-1\right)2\pi /L$, where $j=\mathrm{1,2},\cdots ,L$. Generalizing any order polygon allows for fewer approximation errors with the desired accuracy. Figure 4 shows square (L = 4) and octagon (L = 8) approximations. In this paper, we use the value $L=16$, for which an approximation error in the worst case is 0.5% of the true value [22].

As a result, the inequality (10) can be linearized and written in a matrix form

$${\mathit{A}}_i^1{\mathit{x}}^{\delta }\le {\mathit{b}}_i^1, i=\mathrm{1,2},\cdots ,N_F,$$

(14)

where matrix ${\mathit{A}}_i^1$ and vector ${\mathit{b}}_i^1$ are provided by

$$\begin{gathered} {\mathit{A}}_i^1=\left[\begin{array}{cc}\mathrm{Re}\left\{{\mathit{h}}_i\right\}\cos {\alpha }_{i1}+\mathrm{Im}\left\{{\mathit{h}}_i\right\}\sin {\alpha }_{i1}& -1\\ \mathrm{Re}\left\{{\mathit{h}}_i\right\}\cos {\alpha }_{i2}+\mathrm{Im}\left\{{\mathit{h}}_i\right\}\sin {\alpha }_{i2}& -1\\ ⋮& ⋮\\ \mathrm{Re}\left\{{\mathit{h}}_i\right\}\cos {\alpha }_{iL}+\mathrm{Im}\left\{{\mathit{h}}_i\right\}\sin {\alpha }_{iL}& -1\end{array}\right], \\ {\mathit{b}}_i^1=\left[\begin{array}{c}\mathrm{Re}\left\{g_i\right\}\cos {\alpha }_{i1}+\mathrm{Im}\left\{g_i\right\}\sin {\alpha }_{i1}\\ \mathrm{Re}\left\{g_i\right\}\cos {\alpha }_{i2}+\mathrm{Im}\left\{g_i\right\}\sin {\alpha }_{i2}\\ ⋮\\ \mathrm{Re}\left\{g_i\right\}\cos {\alpha }_{iL}+\mathrm{Im}\left\{g_i\right\}\sin {\alpha }_{iL}\end{array}\right]. \end{gathered}$$

Using matrix notation and collecting inequality linearization systems in all settled frequency points, Equation (14) can be written in the linear form:

$${\mathit{A}}^1{\mathit{x}}^{\delta }\le {\mathit{b}}^1,$$

(15)

where matrix ${\mathit{A}}^1$ and vector ${\mathit{b}}^1$ are provided by

$${\mathit{A}}^1=\left[\begin{array}{c}{\mathit{A}}_1^1\\ {\mathit{A}}_2^1\\ ⋮\\ {\mathit{A}}_{N_F}^1\end{array}\right], {\mathit{b}}^1=\left[\begin{array}{c}{\mathit{b}}_1^1\\ {\mathit{b}}_2^1\\ ⋮\\ {\mathit{b}}_{N_F}^1\end{array}\right].$$

Both considered optimization techniques, linear least-squares minimization and minimax optimization, provide similar results. The minimax optimization technique provides equiripple frequency responses (or errors). However, the linear least-squares minimization task usually allows the faster execution of the optimization algorithm since the computation burden of the constraint linearized system (15) can be higher, especially for larger $L$ values.

2.4. Sidelobe Constraints (Frequency Response Constraints in Stop Bands)

Polynomials $B\left(z\right)$ and $A\left(z\right)$ introduce an increase in the sidelobes of $H_m\left(z\right)$. If we limit the level of the sidelobes under the level of $l_i^{SB},$ we can introduce constraints

$$\left|H_m^{\mathrm{A}\mathrm{B}}\left(\mathit{x},z_i\right)\right|\le l_i^{SB}, i=\mathrm{1,2},\cdots ,N_{SB}.$$

(16)

Since $H^d\left(z_i\right)=0$, we obtain

$${\mathit{g}}_i=\frac{W\left(z_i\right)\left[{\left.{H\left(z_i\right)\mathit{q}}_{\mathit{B}}\right|}_{\mathit{z}=z_i}, {\mathbf{0}}_{1\times N_A}\right]}{\left|A^{\left(k-1\right)}\left(z_i\right)\right|}. i=\mathrm{1,2},\cdots ,N_{SB}.$$

(17)

In this case, Equation (16) can be linearized and written in a matrix form as

$${\mathit{A}}_i^2\mathit{x}\le {\mathit{b}}_i^2, i=\mathrm{1,2},\cdots ,N_{SB},$$

(18)

$${\mathit{A}}_i^2=\left[\begin{array}{c}\left[\mathrm{Re}\left\{{\mathit{g}}_i\right\}\cos {\alpha }_{i1}+\mathrm{Im}\left\{{\mathit{g}}_i\right\}\sin {\alpha }_{i1}\right]\\ \left[\mathrm{Re}\left\{{\mathit{g}}_i\right\}\cos {\alpha }_{i2}+\mathrm{Im}\left\{{\mathit{g}}_i\right\}\sin {\alpha }_{i2}\right]\\ ⋮\\ \left[\mathrm{Re}\left\{{\mathit{g}}_i\right\}\cos {\alpha }_{iL}+\mathrm{Im}\left\{{\mathit{g}}_i\right\}\sin {\alpha }_{iL}\right]\end{array}\right], {\mathit{b}}_i^2=\left[\begin{array}{c}{l}_i^{SB}\\ l_i^{SB}\\ ⋮\\ l_i^{SB}\end{array}\right],$$

where $l_i^{SB}$ is the constraint limit of the error at point $z_i$.

Using matrix notation and collecting inequality linearization systems in all settled frequency points, Equation (18) can be written in the linear form:

$${\mathit{A}}^2\mathit{x}\le {\mathit{b}}^2,$$

(19)

where matrix ${\mathit{A}}^2$ and vector ${\mathit{b}}^2$ are provided by

$${\mathit{A}}^2=\left[\begin{array}{c}{\mathit{A}}_1^2\\ {\mathit{A}}_2^2\\ ⋮\\ {\mathit{A}}_{N_{SB}}^2\end{array}\right], {\mathit{b}}^2=\left[\begin{array}{c}{\mathit{b}}_1^2\\ {\mathit{b}}_2^2\\ ⋮\\ {\mathit{b}}_{N_{SB}}^2\end{array}\right].$$

2.5. Stability Constraint

To ensure the stability of the IIR filter $H^{AB}\left(z\right)$, the stability constraints imposed on the coefficient vector $x_A$ must be taken into account. In [23], a suitable iterative stability condition based on Rouche’s theorem is proposed. This approach to stability condition control during the optimization task is used in [16]. It can be summarized as a condition

$$\left|A^{\left(k\right)}\left(z\right)-A^{\left(k-1\right)}\left(z\right)\right|\le \alpha \left|A^{\left(k-1\right)}\left(z\right)\right|,$$

(20)

or in a matrix notation

$$\left|{\left.{\mathit{q}}_A\right|}_{z=z_i}{\mathit{x}}_{\mathit{A}}-A^{\left(k-1\right)}\left(z_i\right)+1\right|\le \alpha \left|A^{\left(k-1\right)}\left(z_i\right)\right|,$$

(21)

where $\left|z_i\right|=\rho$, $\left(0<\rho <1\right)$ and $0<\alpha <1$.

The simplest choice for the initial value of vector $\mathit{x}$, for which is the initial polynomial of the denominator $A^{\left(0\right)}\left(z\right)$ has all roots inside the circle whose center in the origin of the $z$-plane and has a radius $\rho$, is ${\mathit{x}}^{\left(0\right)}=0$. Inequalities (20) and (21) should be satisfied for a sufficiently dense grid of points dispersed on the circle with radius $\rho \left(\left|z\right|=\rho \right)$.

Collecting constraints (21) for the $N_S$ point lying on the circle with a radius of $\rho \left(\left|z\right|=\rho \right)$ and applying linearization, it follows that

$${\mathit{A}}^3\mathit{x}\le {\mathit{b}}^3,$$

(22)

$${\mathit{A}}^3=\left[\begin{array}{c}{\mathit{A}}_1^3\\ {\mathit{A}}_2^3\\ ⋮\\ {\mathit{A}}_{N_S}^3\end{array}\right], {\mathit{b}}^3=\left[\begin{array}{c}{\mathit{b}}_1^3\\ {\mathit{b}}_2^3\\ ⋮\\ {\mathit{b}}_{N_S}^3\end{array}\right],$$

where matrix ${\mathit{A}}_i^3$ and vector ${\mathit{b}}_i^3$ are provided by

$${\mathit{A}}_i^3=\left[\begin{array}{c}\begin{array}{cc}{\mathbf{0}}_{1\times \left(N_B+1\right)}& \mathrm{R}\mathrm{e}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\cos {\alpha }_{i1}+\mathrm{I}\mathrm{m}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\sin {\alpha }_{i1}\end{array}\\ \begin{array}{cc}{\mathbf{0}}_{1\times \left(N_B+1\right)}& \mathrm{R}\mathrm{e}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\cos {\alpha }_{i2}+\mathrm{I}\mathrm{m}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\sin {\alpha }_{i2}\end{array}\\ ⋮\\ \begin{array}{cc}{\mathbf{0}}_{1\times \left(N_B+1\right)}& \mathrm{R}\mathrm{e}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\cos {\alpha }_{iL}+\mathrm{I}\mathrm{m}\left\{{\left.{\mathit{q}}_{\mathit{A}}\right|}_{z=z_i}\right\}\sin {\alpha }_{iL}\end{array}\end{array}\right],$$

$${\mathit{b}}_i^3=\left[\begin{array}{c}\mathrm{R}\mathrm{e}\left\{A^{\left(k-1\right)}\left(z_i\right)-1\right\}\cos {\alpha }_{i1}+\mathrm{I}\mathrm{m}\left\{A^{\left(k-1\right)}\left(z_i\right)\right\}\sin {\alpha }_{i1}+\alpha \left|A^{\left(k-1\right)}\left(z_i\right)\right|\\ \mathrm{R}\mathrm{e}\left\{A^{\left(k-1\right)}\left(z_i\right)-1\right\}\cos {\alpha }_{i2}+\mathrm{I}\mathrm{m}\left\{A^{\left(k-1\right)}\left(z_i\right)\right\}\sin {\alpha }_{i2}+\alpha \left|A^{\left(k-1\right)}\left(z_i\right)\right|\\ ⋮\\ \mathrm{R}\mathrm{e}\left\{A^{\left(k-1\right)}\left(z_i\right)-1\right\}\cos {\alpha }_{iL}+\mathrm{I}\mathrm{m}\left\{A^{\left(k-1\right)}\left(z_i\right)\right\}\sin {\alpha }_{iL}+\alpha \left|A^{\left(k-1\right)}\left(z_i\right)\right|\end{array}\right].$$

It can be seen that the set of the aforementioned constraint condition (15) is extended by (22). The aforementioned iteration method solves the minimax optimization problem with the modification that it is subject to constraint (22) at each iteration step. This modification ensures that the solution update takes into account the pole radius constraint.

2.6. Constrained Linear Least-Squares (CLLS) Model

Constrained linear least-squares (CLLS) minimizes a linear function called an objective function that is subject to linear constraints. Summarizing the LS task of optimizing the objective function (9) and constraints (19) and (22), the following CLLS problem is obtained:

$$\begin{array}{l}\underset{\mathit{x}}{\min }\frac{1}{2}{‖\mathit{C}\mathit{x}-\mathit{d}‖}_2^2,\\ \mathrm{subject} \mathrm{to} \mathit{A}\mathit{x}\le \mathit{b},\end{array}$$

(23)

where

$$\mathit{A}=\left[\begin{array}{c}{\mathit{A}}^2\\ {\mathit{A}}^3\end{array}\right], \mathit{b}=\left[\begin{array}{c}{\mathit{b}}^2\\ {\mathit{b}}^3\end{array}\right].$$

2.7. Linear Programming (LP) Model

Linear programming (LP) minimizes a linear function called an objective function subject to linear constraints. The following LP problem is formulized:

$$\begin{array}{l}\mathrm{minimize}\hspace{1em}\mathbf{c}{\mathit{x}}^{\delta },\\ \mathrm{subject} \mathrm{to} \mathit{A}{\mathit{x}}^{\delta }\le \mathit{b},\end{array}$$

(24)

where

$$\mathit{A}=\left[\begin{array}{c}{\mathit{A}}^1\\ {\mathit{A}}^{2\delta }\\ {\mathit{A}}^{3\delta }\end{array}\right], {\mathit{A}}^{2\delta }=\left[\begin{array}{cc}{\mathit{A}}^2& 0_{L{N}_{SB}\times 1}\end{array}\right], {\mathit{A}}^{3\delta }=\left[\begin{array}{cc}{\mathit{A}}^3& 0_{L{N}_S\times 1}\end{array}\right], \mathit{b}=\left[\begin{array}{c}{\mathit{b}}^1\\ {\mathit{b}}^2\\ {\mathit{b}}^3\end{array}\right],$$

$$\mathbf{c}=\left[\begin{array}{cc}{\mathbf{0}}_{1\times \left(N_A+N_B+1\right)}& 1\end{array}\right].$$

2.8. Resonators’ Gains Calculation

For known polynomial $A\left(z\right)$, the gain coefficients can be determined directly using Lagrange’s interpolation formula. As a result, the closed-form formulas are obtained [16].

Filter $B\left(z\right)$ can be implemented in different ways. One way is an FIR filter in the serial connection with the basic CR structure. Another way, which is more convenient, is an extension of the CR structure by the resonators with poles generated by the zeros of the polynomial $B\left(z\right)$ [24]. For this purpose, the polynomial $B\left(z\right)$ can be written in the factorized form:

$$B\left(z\right)=b_0\prod _{n=1}^{2M+2}\prod _{i=0}^{K_B}\left(1-z_{M+1+n,i}{z}^{-1}\right),$$

(25)

where $N_B=\left(K_B+1\right)\left(2M+2\right)$ and $\left\{z_{M+1+n,i},n=1,\dots 2M+2,i=0,\dots ,K_B\right\}$ are the roots of $B\left(z\right)$.

A form (25) is convenient for an extension of the CR structure by $2M+2$ branches, each of them consisting of $K_B+1$ resonators, especially in the case $K_B=K,$ when already-derived formulas [16] for $K$-type CR structures are still valid:

$$g_{m,k}^{\prime }=\frac{A\left(z\right)-z^{-1}{P}_m\left(z\right){\sum }_{j=0}^{k-1}\left[g_{m,j}^{\prime }{\prod }_{i=0}^{j-1}\left(1-z_{m,i}{z}^{-1}\right)\right]}{z^{-1}{P}_m\left(z\right)\prod _{i=0}^{k-1}\left(1-z_{m,i}{z}^{-1}\right)}|{}_{z=z_{m,k},}$$

(26)

$$g_{m,k}=g_{m,k}^{\prime }/g_{m,k+1}^{\prime }, \left(g_{m,K+1}^{\prime }=1\right), m=-M,\dots ,0,\dots ,3M+3, k=0,1,\dots ,K,$$

where resonator poles $\left\{z_{m,k},m\in \left[M+2,3\mathrm{M}+3\right],k=0,1,\dots ,K\right\}$ in the added parallel cascades are replicas of the zeros of polynomial $B\left(z\right)$.

The existing formula for calculating gains is only valid for $K_B=K$ and is not valid in other cases. $K_B\ne K$ needs a completely new derivation of this formula.

It is important to note that this formula is only valid for single resonators but not for multiple ones. Since this is about the so-called quasi-MR-based estimator, the poles of the resonator of the same cascade and corresponding to the same harmonic frequency are chosen very close to each other but with a minimum critical distance [14].

3. Computational Complexity

The mother filter bank consists of $2\left(K+1\right)\left(M+1\right)$ resonators. If the compensation polynomial $B\left(z\right)$ is implemented through the extension of the basic resonator structure, the number of resonators is $2\left(K+K_B+2\right)\left(M+1\right).$ In case $K_B=K$, it is $4\left(K+1\right)\left(M+1\right)$. Each resonator needs two complex multiplications in every sample time instant, which means that the total number of complex multiplications is $8\left(K+1\right)\left(M+1\right)$. It should be mentioned that the second part of the algorithm for forming the desired filter banks (summation) does not involve any multiplications. The number of multiplications per one sample time instant as a function of $K$ and $M$ is provided in

Table 1. The number of complex multiplications per one sample time instant as a function of $K$ and $M$.

$\mathit{K}$	$\mathit{M}$ = 7	$\mathit{M}$ = 15	$\mathit{M}$ = 31	$\mathit{M}$ = 63	$\mathit{M}$ = 127
0	64	128	256	512	1024
1	128	256	512	1024	2048
2	192	384	768	1536	3072
3	256	512	1024	2048	4096
4	320	640	1280	2560	5120
5	384	768	1536	3072	6144

and Figure 5.

As the sampling rate in the JPEG standard is 48 kHz, the minimum processing power, depending on K and $M$, in audio applications of this algorithm, is shown in FLOPS (floating point operation per second) in

Table 2. The number of real multiplications according to the JPEG standard as a function of $K$ and $M$.

$\mathit{K}$	$\mathit{M}$ = 7	$\mathit{M}$ = 15	$\mathit{M}$ = 31	$\mathit{M}$ = 63	$\mathit{M}$ = 127
0	$1.23\times {10}^7$	$2.46\times {10}^7$	$4.92\times {10}^7$	$9.83\times {10}^7$	$1.97\times {10}^8$
1	$2.46\times {10}^7$	$4.92\times {10}^7$	$9.83\times {10}^7$	$1.97\times {10}^8$	$3.93\times {10}^8$
2	$3.69\times {10}^7$	$7.37\times {10}^7$	$1.47\times {10}^8$	$2.95\times {10}^8$	$5.90\times {10}^8$
3	$4.92\times {10}^7$	$9.83\times {10}^7$	$1.97\times {10}^8$	$3.93\times {10}^8$	$7.86\times {10}^8$
4	$6.14\times {10}^7$	$1.23\times {10}^8$	$2.46\times {10}^8$	$4.92\times {10}^8$	$9.83\times {10}^8$
5	$7.37\times {10}^7$	$2.95\times {10}^8$	$2.95\times {10}^8$	$5.90\times {10}^8$	$1.18\times {10}^9$

and Figure 6.

Order $K_A$ of the characteristic polynomial $A\left(z\right)$ does not influence the numerical complexity and does not cause additional computational costs. Order $K_B$ of the polynomial $B\left(z\right)$ increases the computational burden significantly. In this sense, it is important to keep $K_B$ as small as possible.

4. Design Examples

In this section, for demonstration purposes, some characteristic examples are shown. In all examples, the following parameters are prescribed: $W\left(z\right)=1,\alpha =0.5,\rho =0.99,$ and ${\mathit{x}}_0=0$. Constraints of the sidelobes in the stop bands are not used (i.e., ${\mathit{A}}^2$ and ${\mathit{b}}^2$ are spare).

In the first attempt, $N_B=0$ and $N_A=\left(K+1\right)\left(2M+2\right)$ are selected. The aim is to reach an optimized solution without an extra calculation cost of $B\left(z\right)$ and manage the optimized frequency responses only by choosing an appropriate characteristic polynomial $A\left(z\right)$. Figure 7 shows that the level of ripples in the passbands is decreased compared to the ripples shown in Figure 3 (corresponding $N_A=N_B=0$, i.e., $A\left(z\right)=1$ and $B\left(z\right)=b_0$) but are still high. A $K=2$-type IIR CR-based filter bank with lower values of $f_S=4 \mathrm{k}\mathrm{H}\mathrm{z}$, $f_1=125 \mathrm{H}\mathrm{z}$, and $M=15$ is shown.

The second attempt is made with $N_A=0$ (i.e., $A\left(z\right)=1$) and $N_B=\left(K+1\right)\left(2M+2\right)$, ${\tau }_B=N_B/2$. Here, the aim is to reach an optimized solution through compensation by FIR filter $B\left(z\right)$ only. This involves extra calculation cost but avoids the need for stability control during the optimization task, which means a significantly simpler design algorithm. Figure 8 shows that, again, the level of ripples in the passbands is decreased in comparison to the ripples shown in Figure 3, but they still exist. It should be mentioned that, in this case, the resulting filter bank is of the FIR type.

Further improvements in the frequency responses of the FIR-type structure can be obtained by an increase in the order $N_B$ of the compensation polynomial filter $B\left(z\right)$. Figure 9 shows the resulting frequency responses for $N_A=0$ (i.e., $A\left(z\right)=1$) and $N_B=2\left(K+1\right)\left(2M+2\right)$, ${\tau }_B=N_B/2$. It is notable that the ripples in the passband are much smaller, and their maximum equals 0.01 dB for two-harmonic-band filters and 0.1 dB for other ones. The higher ripple in the wider-bandwidth filters is due to the influence of the sidelobes of harmonic filters in the primary filter bank, which is not considered during optimization. However, the order of $B\left(z\right)$ is now doubled, doubling the computational burden of the processing, which is a disadvantage compared to the IIR case where the order of the characteristic polynomial $A\left(z\right)$ is increased, causing no additional computational cost.

In the next example (Figure 10), a $K=2$ type IIR CR-based filter bank is shown with $N_A=N_B=\left(K+1\right)\left(2M+2\right),$ ${\tau }_B=N_B$. In this case, the ripples in the passbands are at the same level as in the previous example (even a little bit smaller). However, in this case, the order of the polynomial $B\left(z\right)$ is two times smaller, which means significantly smaller numerical requirements. Figure 11 shows pole-zero maps of the transfer functions $H\left(z\right)$, $A\left(z\right)$ and $B\left(z\right)$.

In the last example (Figure 12), $K=4,$ $f_S=16\mathrm{k}\mathrm{H}\mathrm{z}$, $f_1=125\mathrm{H}\mathrm{z}$, and $M=63$, $N_A=N_B=\left(K+1\right)\left(2M+2\right),$ ${\tau }_B=N_B$ are selected. The maximum ripple in the passband equals 0.1 dB for all bandwidths. In this case, due to higher $K$, the influence of the sidelobes of harmonic filters in the primary filter bank is negligible. Frequency responses of the filters $A\left(z\right)$ and $B\left(z\right)$, shown in the inset figures at the bottom of the figures, have higher amplitudes than for $K=2$. In addition, it is obvious that the analyzers with a higher multiplicity of resonators provide lower side lobes and higher sharpness.

The width of the passbands can be easily adapted online by changing the number of adjacent output signals from the CR structure. The obtained frequency responses show that, with the increase in $K$, amplitudes of the frequency responses of the compensation part are increased, which causes the rise of the primary sidelobes in the stop bands of the filters in the desired filter banks in comparison to basic bank filters. This level of the rise of sidelobes is equal to the magnitude of the frequency response of the transfer function $B\left(z\right)/A\left(z\right)$. The sidelobes can be decreased by including constraints in the optimization task, which will, however, reduce the flatness in the passband. It should be mentioned that the optimization errors depend on the settled value of ${\tau }_B$ and its value is chosen heuristically. The value of ${\tau }_B$ also influences the ratio of amplitudes of frequency responses of $A\left(z\right)$ and $B\left(z\right)$.

5. Suitable Applications of Described Filter Banks

The proposed filter bank has a number of possible applications. The easy online adaptability can be very convenient in applications where a large variability of communication properties exists, such as underwater acoustic communication systems. Here, the following two areas of the application will be discussed.

5.1. Speech Signal Analysis and Speech and Speaker Recognition

The generation of a speech signal by the human speech apparatus is a very complex but mostly researched process. Key information is carried by the frequencies produced by the speech apparatus. In order to recognize the information generated by the speaker, it is necessary to objectively, precisely, and accurately determine (measure) the frequency content of the speech in real-time. If the speech signal sequences of a specific speaker are measured and recorded over a longer period of time, a probabilistic frequency profile of the specific speaker can be formed. As a result, the speaker can be recognized with high probability in real-time. The process of measuring the frequency content of the speech signal in real-time is exactly what the procedure described in this paper enables.

5.2. Fine Audiogram Measurement and Hearing Correction

The standard medical procedure of audiogram measurement involves the generation of a sound signal at fixed logarithmically distributed frequencies. The signal is amplified/attenuated to the threshold of audibility at those frequencies. A gain/loss chart is an audiogram and is used for hearing correction. For objective hearing correction, the frequency content of the current sound signal must be precisely and accurately known in the bands whose central frequencies are those obtained by the audiogram. The proposed procedure enables obtaining the objective content of the sound signal. For fine hearing correction other than the standard 125 Hz, 250 Hz, …, 8 kHz, a much finer and wider audiogram and a corresponding set of center frequencies must be used. Ninety-six center frequencies are now becoming the standard in quality hearing aids. Today, even people with severely impaired hearing can listen to music if the damage was diagnosed before the age of six.

6. Conclusions

In this paper, we presented an approach to the design of complex filter banks based on a mother IIR CR-based structure. Thanks to the high attenuation of the filters of the primary filter bank, especially in the case of resonator structures with a larger number of resonators in the cascade, the design task was reduced to reshaping the frequency responses of the filters in the primary bank. The algorithm simultaneously reshaped the frequency responses of all harmonic filters in the mother filter bank by determining the characteristic polynomial and the common additional FIR compensation part. The optimization was based on linearized models, including stability constraints so that the obtained results could provide the global optimum.

The advantage of this approach concerns the online adaptability of the bandwidths of the filters in the desired bank, which can be easily performed by a simple addition and/or omission of certain output signals of the adjacent channels from the basic filter bank. In addition, the sharpness can be decreased as low as needed. The drawback of this approach is the considerable computational complexity, which could be a possible problem in low-price and low-power applications.

The algorithm can be further improved by considering the sidelobes in the wider bandwidths during optimization, which will decrease the ripple in the passbands.