Design Optimization of Torsional Vibration Absorbers for Heavy-Duty Truck Drivetrain Systems
Abstract
:1. Introduction
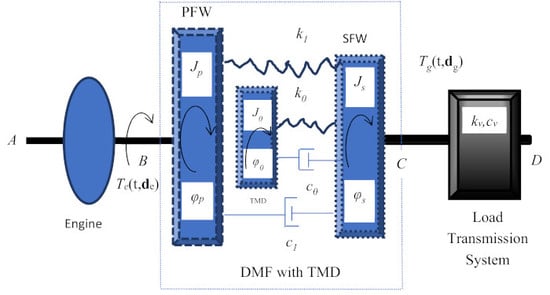
2. Modelling of a Generic Drivetrain System
3. Sensitivity Analysis and Pareto Optimization
Global Sensitivity Analysis and Pareto Optimization Problem Formulations
4. A Drivetrain System Equipped with a Dual Mass Flywheel
4.1. Global Sensitivity Analysis of a Drivetrain System Equipped with a DMF
4.2. Pareto Optimization of a Drivetrain System Equipped with a DMF
5. A Drivetrain System with a Dual Mass Flywheel with a Tuned Mass Damper
5.1. Global Sensitivity Analysis of a Drivetrain System with a DMF with a Tuned Mass Damper
5.2. Pareto Optimization of a Drivetrain System Equipped with a DMF with a Tuned Mass Damper
6. Design Optimization of a DMF and a DMF with a TMD in the Operating Engine Speed Range
7. Results and Discussion
- All the design parameters, significantly affected the level of attenuation of the oscillation of the torque at the transmission input shaft, the friction torque, and the torsional vibration of a DMF.
- The stiffness, i.e., the parameter , most affected the peak-to-peak and the standard deviation of the torsional vibration in the drivetrain system equipped with a DMF, (see sensitivity indices of the objective functionals and in Figure 4, Figure 5 and Figure 6). The torsional stiffness also significantly affected the measures of the torque at the transmission input shaft , as well as the friction torque of the DMF.
- The numerical simulations show that the damping, , affected mostly the friction torque .
- The moment of inertia of the primary flywheel, , had the largest effect on the measures of the torque at the transmission input shaft as well as on the measures of the friction torque for engine speed ne = 800 rpm, (see Figure 4), and its effect decayed with the increasing engine speed.
- Figure 10 and Figure 11 present mappings between the design parameters and total sensitivity indices of the measures of the vibration Dynamics (35) and (36) of the drivetrain system equipped with a DMF with a tuned mass damper. An analysis shows that the moment of inertia, as well as the stiffness coefficients most affected the vibration attenuation and the energy efficiency of the design of the vibration absorber. The stiffness coefficient and the moment of inertia of the tuned mass damper had the largest effect on the considered measures for low engine speed.
- In the case of the design of the vibration absorbers in the operating engine speed range 600–2000 rpm for heavy-duty truck drivetrain systems, the propose objective Functions (44) were the most sensitive with respect to the stiffness and the moment of inertia of the primary flywheel of the DMF, as well as with respect to the stiffness and the moment of inertia of the tuned mass damper (see Figure 15 and Figure 17).
- As shown in the last two columns of Table 2, in the case of the design optimization of the vibration absorber for the prescribed engine speed, the standard deviation of the torque at the transmission input shaft can be decreased significantly (up to three times) by choosing appropriate values of the design parameters of the DMF in comparison to the standard deviation of the torque obtained for the nominal values of design Parameters (40).
- With an increasing engine speed, the attenuation of oscillations of the torque at the transmission input shaft required a higher inertia moment of the primary flywheel and a lower inertial moment of the secondary flywheel (see columns 4 and 5 in Table 2). Therefore, to guarantee an acceptable level of torque oscillations for the whole range of engine speeds, an appropriate trade-off between the values of the moments of inertia of the primary and the secondary flywheels must be chosen.
- The Pareto optimization results, obtained for the prescribed values of engine speed in the range 800–2000 rpm, show that the incorporation of the tuned mass damper into the DMF made it possible to decrease significantly (up to two times) the standard deviation of the torque at the transmission input shaft in comparison to the case of the optimized DMF without a tuned mass damper (see column 6 in Table 2 and the last column in Table 4).
- The choice of objective functions is an important step in the design optimization of vibration absorbers for heavy-duty truck drivetrain systems. The proposed objective Functions (44) seemed to be suitable for optimizing a DMF and a DMF with a tuned mass damper in the operating engine speed range. Using these objective functions, it was shown that for the drivetrain system equipped with DMF and with the DMF with a TMD, there exists a trade-off between the vibration attenuation and the energy efficiency (see Figure 18).
- An evaluation of the objective function for the nominal and optimized values of the design parameters of a DMF (Parameters (40) and (47)), makes it possible to compare quantitatively the obtained engine speed history of the standard deviation of the torques at the transmission input shaft for a nominal and an optimized DMF. The results show that the efficiency of the attenuation of the oscillations of the torque at the transmission input shaft increased by up to 40% in comparison to the performance of the DMF with nominal design parameters.
- An analysis of the obtained solution of the Pareto optimization problem in the operating engine speed range 600–2000 rpm for the DMF with a TMD reveals that within the frame of considered assumptions, the incorporation of a TMD into a DMF enhanced the performance of the vibration absorber in comparison to the optimized DMF without a TMD (see blue and red curves in Figure 16).
8. Conclusions and Outlook
- There existed a clear trade-off between the measure of the oscillations attenuation of the torque at the transmission input shaft and the measure of the energy efficiency in the design of torsional vibration absorbers for heavy-duty truck drivetrain systems both in the case of a DMF and in the case of a DMF with a tuned mass damper.
- For a heavy-duty truck drivetrain system equipped with a DMF, the optimized mass inertia, stiffness, and damping parameters provided the best attenuation of oscillations of the torque at the transmission input shaft in the operating engine speed range 600–2000 rpm when the third engine order vibration harmonic was in focus.
- The incorporation of a torsional tuned mass damper into a DMF with the appropriate optimization of design parameters can significantly enhance the performance of the combined vibration absorber. For instance, for the operating engine speed range 800–1200rpm, the utilization of the TMD in the DMF decreased up to two times the standard deviation of the torque at the transmission input shaft in comparison to the standard deviation of the torque in the case of the optimized DMF without a tuned mass damper.
- The global sensitivity analysis and Pareto optimization were proven to be efficient for advanced analysis and design of torsional vibration absorbers for drivetrain systems. The results obtained are evidence of the feasibility of the application of dual mass flywheels in heavy-duty truck drivetrain systems.
Funding
Acknowledgments
Conflicts of Interest
References
- Haddow, A.; Shaw, S. Centrifugal Pendulum Vibration Absorbers: An Experimental and Theoretical Investigation. Nonlinear Dyn. 2003, 34, 293–307. [Google Scholar] [CrossRef]
- Wellmann, T.; Govindswamy, K.; Braun, E.; Wolff, K. Aspects of Driveline Integration for Optimized Vehicle NVH Characteristics. In Proceedings of the Noise and Vibration Conference and Exhibition, St. Charles, IL, USA, 15–17 May 2007. SAE Technical Paper. [Google Scholar]
- Park, T.; Song, J.; Jang, J.; Joo, I. Dynamic Analysis of Damper System in Torque Converter. In Proceedings of the Asia Pacific Automotive Engineering Conference, California, CA, USA, 5–8 August 2007; SAE Technical Paper. pp. 1–7. [Google Scholar]
- Struggl, S.; Berbyuk, V.; Johansson, H. Review on wind turbines with focus on drive train system dynamics. Wind Energy 2015, 18, 567–590. [Google Scholar] [CrossRef]
- Habib, G.; Kerschen, G. A principle of similarity for nonlinear vibration absorbers. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, IDETC/CIE 2015, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Chaithanya, D.; Narayanasamy, A. Engine Flywheel Failure Avoidance through CAE Optimization. In Proceedings of the WCXTM 17: SAE World Congress Experience, Detroit, ML, USA, 4–6 April 2017; SAE Technical Paper. pp. 1–7. [Google Scholar]
- Gupta, K.; Choudhary, A.; Bidre, R. NVH Performance Improvement Study Using a Dual Mass Flywheel (DMF), Inertia Ring Type Tuned Torsional Vibration Damper (TVD) and Single Mass Flywheel (SMF) in a Front Engine and Rear Wheel Driveline Architecture. In Proceedings of the Noise and Vibration Conference and Exhibition, Monroe Village, NW, USA, 12–15 June 2017; SAE Technical Paper. pp. 1–8. [Google Scholar]
- Mall, P.; Fidlin, A.; Krüger, A.; Groß, H. Simulation based optimization of torsional vibration dampers in automotive powertrains. Mech. Mach. Theory 2017, 115, 244–266. [Google Scholar] [CrossRef]
- Wramner, L. Torsional vibrations in truck powertraines with dual mass flywheel having piecewise linear stiffness. In Proceedings of the 9th European Nonlinear Dynamics Conference, ENOC 2017, Budapest, Hungary, 25–30 June 2017; pp. 1–10. [Google Scholar]
- Wramner, L.; Berbyuk, V.; Johansson, H. Vibration dynamics in non-linear dual mass flywheels for heavy-duty trucks. In Proceedings of the 28th edition of the Biennial ISMA conference on Noise and Vibration Engineering, Leuven, Belgium, 17–19 September 2018; pp. 1863–1876. [Google Scholar]
- Haris, A.; Motato, E.; Theodossiades, S.; Rahnejat, H.; Kelly, P.; Vakakis, A.; Bergman, L.; McFarland, D.M. A study on torsional vibration attenuation in automotive drivetrains using absorbers with smooth and non-smooth nonlinearities. Appl. Math. Modelling 2017, 46, 674–690. [Google Scholar] [CrossRef]
- Shi, C.; Parker, R.G.; Shaw, S.W. Tuning of Centrifugal Pendulum Vibration Absorbers for Translational and Rotational Vibration Reduction. Mech. Mach. Theory 2013, 66, 56–65. [Google Scholar] [CrossRef]
- Shi, C.; Shaw, S.W.; Parker, R.G. Vibration Reduction in a Tilting Rotor Using Centrifugal Pendulum Vibration Absorbers. J. Sound Vib. 2016, 385, 55–68. [Google Scholar] [CrossRef]
- Keeney, C.S.; Shih, S. Prediction and Control of Heavy Duty Powertrain Torsional Vibration. J. Commer. Vehicles 1992, 101, 805–814. [Google Scholar]
- Tan, X.; Hua, L.; Lu, C.; Yang, C.; Wang, Y.; Wang, S. A new method for optimizing the parameters of torsional vibration dampers. J. Vibroeng. 2017, 19, 4155–4171. [Google Scholar]
- Song, L.Q.; Zeng, L.P.; Zhang, S.P.; Zhou, J.D.; Niu, H.E. Design and analysis of a dual mass flywheel with continuously variable stiffness based on compensation principle. Mech. Mach. Theory 2014, 79, 124–140. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, R.; Jiang, Z. Nonlinear dynamical model of an automotive dual mass flywheel. Adv. Mech. Eng. 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Fidlin, A.; Mall, P. On the effect of the distributed friction in the arc spring on the dynamic behavior of the automotive transmission. In Proceedings of the International Conference on Engineering Vibrations, ICoEV, Ljubljana, Slovenia, 7–10 September 2015; pp. 1099–1108. [Google Scholar]
- Faust, H. Powertrain systems of the future—engine, transmission and damper systems for downspeeding, downsizing and cylinder deactivation. In Proceedings of the Schaeffler Symposium, Baden-Baden, Germany, 3–4 April 2014; pp. 24–41. [Google Scholar]
- Wramner, L. Dual Mass Flywheels in Truck Powertrains: Modelling, Simulations and Validation. Licentiate Thesis, Department of Mechanics and Maritime Sciences, Chalmers University of Technology, Göteborg, Sweden, December 2018; p. 32. [Google Scholar]
- Wramner, L. Torsional vibrations in heavy-duty truck powertrains with dual mass flywheels. Int. J. of Heavy Vehicle Systems 2019. Submitted. [Google Scholar]
- Karimaei, H.; Mehrgou, M.; Chamani, H.R. Optimisation of torsional vibration system for a heavy-duty inline six-cylinder diesel engine. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2019, 1–15. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; Dover Publication, Inc.: New York, NY, USA, 1985. [Google Scholar]
- Lindell, H.; Berbyuk, V.; Josefsson, M.; Grétarsson, S. Nonlinear dynamic absorber for reduce vibration in hand-held impact machines. In Proceedings of the International Conference on Engineering Vibration, Ljubljana, Slovenia, 7–10 September 2015; pp. 1530–1539. [Google Scholar]
- Detroux, T.; Habib, G.; Masset, L.; Kerschen, G. Performance, robustness and sensitivity analysis of the nonlinear tuned vibration absorber. Mech. Syst. Signal Process. 2015, 60–61, 799–809. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthquake Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthquake Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar]
- De Domenico, D.; Impollonia, N.; Ricciardi, G. Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthquake Eng. 2018, 105, 37–53. [Google Scholar] [CrossRef]
- Fidlin, A.; Seebacher, R. DMF simulation techniques—Finding the needle in the haystack. In Proceedings of the LuK Symposium, Baden, Austria, 4–5 May 2006; pp. 55–70. [Google Scholar]
- Shaw, S. Designing Nonlinear Torsional Vibration Absorbers. In Exploiting Nonlinear Behavior in Structural Dynamics; Wagg, D., Virgin, L., Eds.; Springer: Wien, Austria, 2012; pp. 135–169. [Google Scholar]
- Mousavi Bideleh, S.M.; Berbyuk, V. A Computer Code for Sensitivity Analysis and Multiobjective Optimization: SAMO Tutorial; Department of Mechanics and Maritime Sciences, Chalmers University of Technology: Gothenburg, Sweden, 2017; Report No. 1; pp. 1–45. [Google Scholar]
- Mousavi Bideleh, S.M.; Berbyuk, V. Global sensitivity analysis of bogie dynamics with respect to suspension components. Multibody Syst. Dyn. 2016, 37, 145–174. [Google Scholar] [CrossRef]
- Mousavi Bideleh, S.M.; Berbyuk, V. Multiobjective optimisation of bogie suspension to boost speed on curves. Vehicle Syst. Dyn. 2016, 54, 58–85. [Google Scholar] [CrossRef]
- Mousavi Bideleh, S.M.; Berbyuk, V. Pareto Optimization of a Nonlinear Tuned Mass Damper to Control Vibrations in Hand Held Impact Machines. In Nonlinear Dynamics, Volume 1. Conference Proceedings of the Society for Experimental Mechanics Series; Kerschen, G., Ed.; Springer: Cham, Germany, 2018; pp. 27–44. [Google Scholar]
- Zhang, X.; Pandey, M.D. An effective approximation for variance-based global sensitivity analysis. Reliability Eng. Syst. Safety 2014, 121, 164–174. [Google Scholar] [CrossRef]
- Rabitz, H.; Alis, Ö. General foundations of high-dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method. Struct. Safety 2013, 43, 28–40. [Google Scholar]
- Zu, Q.-H.; Chen, Z.-Y.; Shi, W.-K.; Mao, Y.; Chen, Z.-Y. Torsional Vibration Semiactive Control of Drivetrain Based on Magnetorheological Fluid Dual Mass Flywheel. Math. Probl. Eng. Hindawi Publ. Corp. 2015, 608737. [Google Scholar] [CrossRef]
- Karlsson, J. Investigation of Dynamic Friction Properties of a Dual Mass Flywheel for Commercial Vehicles. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, June 2018. [Google Scholar]


















| Design Parameter, d | k1 Nm/rad | c1 Nms/rad | Jp kgm2 | Js kgm2 |
|---|---|---|---|---|
| Nominal value of d | 12,732 | 30 | 1.8 | 0.9 |
| Lower bound, d | 10,312 | 0 | 0.2 | 0.1 |
| Upper bound, d | 26,242 | 100 | 3.6 | 2 |
| ne Rpm | Nm/rad | Nms/rad | kgm2 | kgm2 | Min std(Tg[q(t),d]) Nm | Nom std(Tg[q(t), d]) Nm |
|---|---|---|---|---|---|---|
| 800 | 10,501 | 51 | 3.6 | 0.1 | 33 | 92 |
| 1000 | 10,503 | 50 | 3.5 | 0.1 | 28 | 126 |
| 1200 | 11,157 | 64 | 3.4 | 2.0 | 23 | 127 |
| 1400 | 10,854 | 85 | 3.4 | 1.9 | 19 | 38 |
| 1600 | 10,867 | 88 | 2.3 | 2.0 | 17 | 25 |
| 1800 | 11,228 | 94 | 2.1 | 1.7 | 16 | 22 |
| 2000 | 11,218 | 94 | 1.7 | 1.6 | 15 | 21 |
| Design Parameter, d | k1 Nm/rad | c1 Nms/rad | Jp kgm2 | Js kgm2 | k0 Nm/rad | J0 kgm2 | c0 Nms/rad |
|---|---|---|---|---|---|---|---|
| Initial value of d | 10,501 | 51 | 3.60 | 0.1 | 8000 | 0.1 | 0.02 |
| Lower bound, d | 10,312 | 0 | 0.2 | 0.1 | 5000 | 0.05 | 0.01 |
| Upper bound, d | 26,242 | 100 | 3.6 | 2 | 12,732 | 0.4 | 0.08 |
| ne Rpm | Nm/rad | Nms/rad | kgm2 | kgm2 | Nm/rad | kgm2 | Nms/rad | Min std(Tg[q(t), d]) Nm |
|---|---|---|---|---|---|---|---|---|
| 800 | 10,828 | 74 | 2.2 | 0.7 | 8898 | 0.14 | 0.03 | 16 |
| 1000 | 11,954 | 93 | 1.8 | 0.9 | 10,310 | 0.10 | 0.02 | 13 |
| 1200 | 11,876 | 92 | 2.8 | 0.8 | 7941 | 0.06 | 0.07 | 13 |
| 1400 | 10,969 | 71 | 3.3 | 1.7 | 10,247 | 0.11 | 0.7 | 20 |
| 1600 | 10,867 | 88 | 2.4 | 2.0 | 8000 | 0.06 | 0.04 | 16 |
| 1800 | 11,063 | 91 | 2.4 | 1.8 | 8795 | 0.05 | 0.05 | 15 |
| 2000 | 10,965 | 93 | 2.1 | 1.4 | 8841 | 0.07 | 0.04 | 15 |
| Design Parameter, d | k1 Nm/rad | c1 Nms/rad | Jp kgm2 | Js kgm2 |
|---|---|---|---|---|
| Nominal value of d | 12,732 | 30 | 1.8 | 0.9 |
| Lower bound, d | 10,312 | 0 | 0.9 | 0.45 |
| Upper bound, d | 26,242 | 100 | 2.7 | 1.35 |
| Design Parameter, d | k1 Nm/rad | c1 Nms/rad | Jp kgm2 | Js kgm2 | k0 Nm/rad | J0 kgm2 | C0 Nms/rad |
|---|---|---|---|---|---|---|---|
| Initial value, d | 12,732 | 30 | 1.8 | 0.9 | 7785 | 0.31 | 0.05 |
| Lower bound, d | 10,312 | 0 | 0.9 | 0.45 | 5000 | 0.05 | 0.01 |
| Upper bound, d | 26,242 | 100 | 2.7 | 1.35 | 12,732 | 0.9 | 0.2 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berbyuk, V. Design Optimization of Torsional Vibration Absorbers for Heavy-Duty Truck Drivetrain Systems. Vibration 2019, 2, 240-264. https://doi.org/10.3390/vibration2030015
Berbyuk V. Design Optimization of Torsional Vibration Absorbers for Heavy-Duty Truck Drivetrain Systems. Vibration. 2019; 2(3):240-264. https://doi.org/10.3390/vibration2030015
Chicago/Turabian StyleBerbyuk, Viktor. 2019. "Design Optimization of Torsional Vibration Absorbers for Heavy-Duty Truck Drivetrain Systems" Vibration 2, no. 3: 240-264. https://doi.org/10.3390/vibration2030015