Electroviscoelstic Stability Analysis of Cylindrical Structures in Walters B Conducting Fluids Streaming through Porous Medium

Abstract

In this research, the linear stability of a cylindrical interface between two viscoelstic Walters B conducting fluids moving through a porous medium is investigated theoretically and numerically. The fluids are influenced by a uniform axial electric field. The cylindrical structure preserves heat and mass transfer across the interface. The governing equations of motion and continuity are linearized, as are Maxwell’s equations in quasi-static approximation and the suitable boundary conditions at the interface. The method of normal modes has been used to obtain a quadratic characteristic equation in frequency with complex coefficients describing the interaction between viscoelstic Walters B conducting fluids and the electric field. In light of linear stability theory, the Routh–Hurwitz criteria are used to govern the structure’s stability. Several special cases are recoverd under suitable data choices. The stability analysis is conferred in detail via the behaviors of the applied electric field and the imaginary growth rate part with the wavenumbers. The effects of various parameters on the interfacial stability are theoretically presented and illustrated graphically through two sets of figures. Our results demonstrate that kinematic viscosities, kinematic viscoelasticities, and medium porosity improve stability, whereas medium permeability, heat and mass transfer coefficients, and fluid velocities decrease it. Finally, electrical conductivity has a critical influence on the structure’s stability.

1. Introduction

Kelvin–Helmholtz instability (KHI) is one of the most well known instabilities in geophysical, astrophysical, and laboratory areas [1]. KHI appears at the interface separating two superposed fluids streaming with different velocities and densities. As a result of its relationship with types of astrophysical phenomena, chemical engineering, and fluid dynamics involving a shear current, it has been examined by a great number of contributors. Linear KHI has been discussed in Chandrasekhar’s monograph [2]. The effect of flow is disturbed in linear KHI problems. The nonlinear KHI for packets of waves has been discussed before by Weissman [3]. The linear and nonlinar developments of KHI of cylindrical structures of dielectric and conducting fluids in different situations has been investigated in several studies. For instance, Choudhury [4] discussed the nonlinear evolution of the KHI of turbulent tangential velocity discontinuities. Funada et al. [5] analysed the stability of stratified gas–liquid flow in a horizontal rectangular channel under the effect of surface tension and viscosity on the normal stress using viscous potential flow. Chong et al. [6] studied the linear development rate for Kelvin–Helmholtz instability in a moving mixing layer. Asthana et al. [7] determined the Kelvin–Helmholtz instability of viscous potential flow in a cylindrical channel with heat and mass transfer. Hoshoudy et al. [8] analytically investigated the influence of density and velocity gradients on the Kelvin–Helmholtz instability (KHI) of two stacked finite-thickness fluid layers.

Electrohydrodynamics (EHD) can be seen as a class of fluid mechanics concerned with the effects of electric forces, or alternatively as the class of EHD concerned with the influence of fluid flow on electrical fields. As a result, the interactions (electric fields with polarized or free charges) in fluids are taken into account. A review of the EHD topic with an emphasis on several recent advancements has been presented by David [9]. In dielectric fluids, both gravity and surface tension are necessary, and surface waves arise when capillary waves and gravity combine to create a single wave that has both effects. By comparison, the effect of an applied electric field during conducting fluid flow has many characteristics, along with numerous engineering and physical applications. EHD surface waves arise when surface charges engage in the flow of fluids. Many authors have reviewed the role of interfacial stresses on EHD characteristics. Melcher and Taylor [10] considered the effect of electrohydrodynamic instability on interfacial shear stresses. Saville [11] examined the electrohydrodynamics instability of the Taylor–Melcher leaky dielectric model. The commencement of electrohydrodynamic motion caused by the application of an electric field over a thin layer of liquid has been studied by Baygents et al. [12] for a scenario in which the electrical conductivity changes linearly throughout the depth of the layer. Finally, Rudraiah and Chiu-On Ng [13] have reported on the significance of nano-sized smart materials in structural engineering, biological engineering, and military applications.

Several studies in linear EHD stability theory show a tendency to examine uncharged jets in a uniform axial field. Elhefnawy and Moatimid [14] explored the influence of an axial electric field on the stability of cylindrical flows in the presence of mass and heat transfer, and the absence of gravity. Through vertical cylindrical porous inclusions with permeable boundaries, three-dimensional viscous potential electrohydrodynamic Kelvin–Helmholtz instability was examined by Moatimid and Hassan [15]. Awasthi [16] performed a linear analysis of capillary instability in a cylindrical interface between two viscous and dielectric fluids when the fluids are exposed to a continuous axial electric field and there is heat and mass transfer across the contact. They observed that the axial electric field has a stabilizing effect, while the radial one has a dual rule (stabilizing and destabilizing) on the system’s stability. Awasthi and Agrawal [17] presented an analysis of the capillary instability of electroviscous potential flow. Then, they revisited the analysis in their study of [18] as they analysed the capillary instability with radial electric field of viscous potential flow. Li et al. [19] conducted a linear investigation of the axisymmetric and non-axisymmetric instability of a viscous coaxial jet in a radial electric field. In addition, they studied the temporal linear instability of a coaxial jet with two immiscible Newtonian liquids in both the axial and radial electric fields in [20]. The stability problem becomes more intriguing, although more challenging, if the uniform conductivity of fluids is taken into account. Surface charges are crucial in such cases, as conduction in the interface area plays a significant role in many electrical systems. El-Sayed et al. [21] investigated the influence of an applied electric field on the stability of an interface between two thin viscous leaky dielectric fluid layers in a porous medium within the long-wave limit. In addition, they performed a linear stability analysis of a two-dimensional incompressible leaky dielectric viscous liquid sheet surrounded by a hydrodynamically passive conducting medium when an electric field is applied parallel to the originally flat bounding fluid boundaries, admitting surface charges as well [22]. Mestel [23,24] analysed the electrohydrodynamic stability of a slightly and highly viscous jet, respectively, in his studies. Ganan-Calvo [25] investigated electrohydrodynamically-driven (EHD) capillary jets in the parametrical limit of negligible charge relaxation effects, i.e., when the electric relaxation time of the liquid is tiny compared to the hydrodynamic rates. Ozen et al. [26] examined the linear electrohydrodynamic stability of two immiscible fluids in channel flow. Many authors have recently investigated the EHD stability of the interface between conducting fluids in linear and nonlinear cylindrical structures. Keeping this in view, Gonzalez et al. [27] presented a temporal linear modal stability analysis for conducting viscous liquid jets moving with nonzero velocity relative to an ambient gas and exposed to an alternating radial electric field. Lopez-Herrera et al. [28] performed a temporal linear modal stability analysis on poorly-conducting viscous liquid jets flowing relative to a steady radial electric field. Only axisymmetric perturbations resulting in high-quality aerosols were considered. Elhefnawy et al. [29] analysed the nonlinear electrohydrodynamic stability of a finitely-conducting jet in an axial electric field. Elhefnawy et al. [30] investigated the weakly nonlinear streaming instability of two conducting fluids in a cylindrical circular cross-section interface.

When regarding two fluid flows separated by an interface, the interfacial stability problem is commonly examined with the assumption that the fluids are immiscible. A very extensive analysis of inviscid fluids with interfacial heat and mass transfer has been carried out by Hsieh [31,32]. The KHI problem of a liquid/vapor cylindrical interface with heat and mass transfer was formulated by Nayak and Chakraborty [33]. Kim et al. [34] investigated capillary instability in the context of heat and mass transmission and discovered that it resists the growth of disturbance waves. Awasthi et al. [35] investigated the nonlinear KHI of cylindrical flows using viscous potential flow theory. For recent reviews on the subject of EHD instability problems in a cylindrical interface between two fluids with mass and heat transfer see, e.g., El-Sayed et al. [36,37,38]. Tiwari et al. [39] studied electrohydrodynamic capillary instability with heat and mass transfer, which they then revisited in a later study [40] accounting for the effect of free surface charge.

The flow of fluids through porous media is of great interest, as it is quite common in nature. Such flows have many scientific, engineering, and geophysical applications [41,42,43]. Because of this wide interest in engineering and physical applications, KHI in flows in porous media has sparked a great deal of attention in the scientific literature. For current reviews on linear and nonlinear EHD flows in porous media in planar and cylindrical geometries. For instance, Moatimid and Hassan [44] considered the linear electrohydrodynamic KHI of a fully saturated porous interface between two dielectric fluids in the presence of a horizontal electric field with heat and mass transfer. El-Sayed et al. [45] performed a weakly nonlinear stability analysis of wave propagation in three dimensions in two superposed dielectric fluids streaming through porous media in the presence of a vertical electric field creating surface charges. Amer and Moatimid [46] studied the electrohydrodynamic instability of a flowing dielectric liquid jet in which an incompressible Newtonian viscous fluid occupies the inner medium, while the outer medium is simultaneously filled with an incompressible gas.

In addition, during the last few decades non-Newtonian viscous fluids have become increasingly essential in industry. Among these fluids are liquids of different types, including Walters B fluid. This fluid reflects the cumulative effects of many blood parameters, such as red blood cell deformation, plasma viscosity, agglutination, and hematocrits. Walters B fluid has great importance in many industrial applications. Plastic sheet extrusion, fabrication of adhesive tapes, and applying coatings to hard surfaces are a few examples. Studying this fluid in the context of fluid flow problems is both technologically important and a challenge for applied mathematicians and engineers who are interested in obtaining accurate exact solutions. Therefore, in Walters B viscoelastic fluid, the usual viscous term is replaced by the resistive term $-(\rho /k_1)[v-{\nu }^{\prime }\frac{\partial }{\partial t}]\mathbf{v}$, where $\rho$ is the fluid density, $k_1$ is the medium permeability, $\mathbf{v}$ is the Darcician filter velocity, and $\nu$ and ${\nu }^{\prime }$ are the kinematic viscosity and kinematic viscoelasticity, respectively [47]. Walters [48] reported that a mixture of polymethyl methacrylate and pyridine at 25 °C containing 30.5 g of polymer/litre with density 0.98 g/litre behaves very nearly the same as Walters B viscoelastic fluid. Polymers are used in the manufacture of spacecraft, aeroplanes, tyres, belt conveyers, ropes, cushions, seats, foams, plastics engineering equipment, contact lenses, and more. Walters B viscoelastic fluid forms the basis for the manufacture of many such important and useful products.

Due to the great industrial and technological importance of Walters B viscoelastic fluids, the interest in their study has increased in recent decades. Sharma et al. [47] investigated the instability of viscoelastic Walters B fluid flow in a porous medium. They found that in a particular two-dimensional case, the system could be either stable or unstable depending on the kinematic viscosity, medium permeability, and medium porosity. The Rayleigh–Taylor instability (RTI) of two stratified Walters B viscoelastic superposed fluids was investigated by Kumar and Singh [49]. In a stable stratification case, the system seems to be stable according to certain conditions. In addition, they found that the growth rates decrease and increase with increasing kinematic viscosity and kinematic viscoelasticity, respectively. El-Sayed et al. [50,51] studied the nonlinear KHI of two semi-infinite Walters B viscoelastic dielectric fluids streaming in porous media in three dimensions under varied (horizontal or vertical) electric fields with or without surface charges at their interface. Recently, Moatimid and Zekry [52] examined the nonlinear instability of two dielectric viscoelastic Walters B fluids streaming through a vertical cylinder under a uniform axial electric field, introducing multiple time scales in their analysis. A Ginzburg–Landau equation was derived to control the nonlinear behavior of the surface deflection. Moatimid et al. [53] investigated the effect of a uniform electric field on a cylindrical streaming sheet through a porous medium in the presence of uniform, homogeneous, and isotropic media using viscous potential theory.

Taking into account the great variety of physical and engineering applications of viscoelastic Walters B fluids in contemporary technology, the present paper aims to investigate the linear stability of two electrically conducting cylinderical Walters B viscoelastic fluids with rigid boundaries streaming through a porous medium under a uniform axial electric field. The uniform flow is investigated in the presence of heat and mass transfer. Using the normal modes technique and appropriate boundary conditions, analytical solutions for structure parameters are obtained. The effects of different physical parameters on the streaming fluids is plotted graphically. The stability analysis is discussed in detail via the behaviors of the applied electric field and the imaginary growth rate part with the wavenumbers. All of the results obtained herein are new and confirm the former results. The problem discussed here, to the best of our knowledge, has not been investigated yet for conducting fluids in presence of heat and mass transfer.

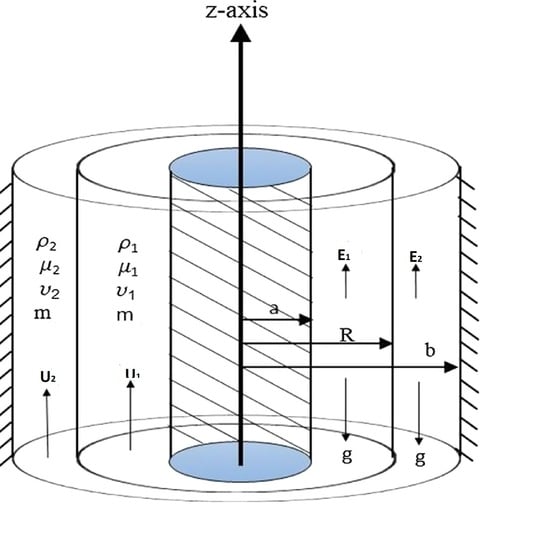
2. Flow Description

2.1. Basic Equations

Assume an undisturbed cylindrical interface $r=R$ separating two infinite Walters B viscoelastic conducting fluids confined between two concentric circular rigid cylinders. Applying the cylindrical coordinates $(r,\theta ,z)$, where the z-axis is the symmetry axis in the equilibrium case, the central solid core has a radius $R_1$ and the outer cylinder has a radius $R_2$, where $R_1<R<R_2$. Fluid (1) fills the inner cylinderical region $R_1<r<R,$ while fluid (2) fills the outer region $R<r<R_2$. The two fluids flow with vertical uniform velocities $U_1$ and $U_2$ along the z-axis through a porous medium, and are affected by a constant axial electric field $E_0$ acting along the z-direction. Keeping in mind the presence of surface tension T between the two fluids, we denote by ${\rho }_j,$${\epsilon }_j$, ${\sigma }_j$, ${\mathbf{E}}_j$, m and ${\lambda }_1$, $(j=1,2)$ the fluid densities, dielectric constants, electrical conductivities, electric field elements, and the porosity and permeability of the medium, respectively. The temperatures at $r=R_1$, $r=R$, and $r=R_2$ are taken as $T_1$, $T_0$, and $T_2$, respectively [14]. A sketch of the physical problem is shown in Figure 1.

Assuming the disturbances in the system are axisymmetric, the equations of motion and continuity for Walters B viscoelastic fluid flows through a porous medium are [50]

$$\frac{\rho }{m}\left[\frac{\partial \mathbf{v}}{\partial t}+\frac{1}{m}(\mathbf{v}·\nabla )\mathbf{v}\right]=-\nabla p-\rho \mathbf{g}-\frac{\rho }{{\lambda }_1}[\nu -{\nu }^{\prime }\frac{\partial }{\partial t}]\mathbf{v}$$

(1)

$$\nabla .\mathbf{v}=0,$$

(2)

where $p,\nu ,$${\nu }^{\prime }$, and $\mathbf{g}$ respectively denote the hydrostatic pressure, kinematic viscosity, kinematic viscoelasticity, and acceleration due to gravity acting in the negative z-direction. Assuming the motion of the two fluids is irrotational, the velocities can be written as the gradient of the potential functions ${\mathrm{\Phi }}_j(r,z,t)$ such that ${\mathbf{v}}_j=U_j+\nabla {\mathrm{\Phi }}_j$, $j=1,2$, where $\mathbf{v}$ is the fluid velocity, t is the time, and $\nabla =\left(\partial /\partial r,r^{-1}\partial /\partial \theta ,\partial /\partial z\right)$. The potentials ${\mathrm{\Phi }}_j$ and $j=1,2$ satisfy Laplace’s equation [14]

$${\nabla }^2{\mathrm{\Phi }}_1=0\mathrm{for}{R}_1<r<R+\eta ,-\infty <z<\infty$$

(3)

$${\nabla }^2{\mathrm{\Phi }}_2=0\mathrm{for}R+\eta <r<R_2,-\infty <z<\infty$$

(4)

where $\nabla {\mathrm{\Phi }}_j\to 0$ as $z\to \pm \infty ,$${\nabla }^2=\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{{\partial }^2}{\partial z^2}$ and $\eta =\eta (z,t)$ is the disturbance in the radius of the interface from its equilibrium value R,

$$r=R+\eta (z,t)$$

(5)

In EHD, the magnetic effects are very small; thus, the quasi-static electric field is assumed. Hence, the electrical Maxwell’s equations are

$$\nabla \times \mathbf{E}=\mathbf{0},\nabla .\left(\epsilon \mathbf{E}\right)=q$$

(6)

The charge conservation equation [10] is

$$\nabla ·\mathbf{J}+\frac{\partial q}{\partial t}=0$$

(7)

where $\mathbf{J}=\sigma \mathbf{E}+q$$\mathbf{v}$, is the free current density, q is the free charge density, and $\sigma$ is the electrical conductivity. Therefore, the electric field can be represented as the gradient of the electrostatic potentials ${\mathrm{\Psi }}_j(r,z,t)$:

$${\mathbf{E}}_j=E_0{\mathbf{e}}_z-\nabla {\mathrm{\Psi }}_j,(\mathrm{j}=1,2)$$

(8)

From Equations (6) and (8), the scalar electric potentials ${\mathrm{\Psi }}_j$, $j=1,2$ satisfy Laplace’s equation:

$${\nabla }^2{\mathrm{\Psi }}_1=0\mathrm{in}{R}_1<r<R+\eta ,-\infty <z<\infty$$

(9)

$${\nabla }^2{\mathrm{\Psi }}_2=0\mathrm{in}R+\eta <r<R_2,-\infty <z<\infty$$

(10)

where $\nabla {\mathrm{\Psi }}_j\to 0$, as $z\to \pm \infty .$ The solutions of ${\mathrm{\Phi }}_j$ and ${\mathrm{\Psi }}_j$, ($j=1,2)$, should satisfy the boundary conditions below.

2.2. Boundary Conditions

• On a rigid cylindrical surface, the velocity potentials ${\mathrm{\Phi }}_j$ and the electric potentials ${\mathrm{\Psi }}_j$$(j=1,2)$ must satisfy the following conditions [14]:

  $$\frac{\partial {\mathrm{\Phi }}_1}{\partial r}=\frac{\partial {\mathrm{\Psi }}_1}{\partial z}=0\mathrm{on}r=R_1$$

  (11)

  $$\frac{\partial {\mathrm{\Phi }}_2}{\partial r}=\frac{\partial {\mathrm{\Psi }}_2}{\partial z}=0\mathrm{on}r=R_2$$

  (12)
• At the interface $r=R+\eta (z,t)$, the tangential electric field component is assumed to be continuous [14]:

  $$∥{\mathrm{\Psi }}_z∥+{\eta }_z∥{\mathrm{\Psi }}_r∥=0,$$

  (13)

  where $∥f∥=f_2-f_1$ define the jump of the quantity f over the interface $S=r-R-\eta (z,t)$ between the two fluids.
• When the uniform conductivity of fluids is taken into account, the problem becomes more attractive, though more challenging as well. In many electrical structures, surface charges and conduction in the interface region play a crucial role. The continuity of stationary current normal to the interface $r=R+\eta (z,t)$ should lead to charge accumulation on the interface [10,23]. At steady state, we obtain the following condition:

$${\eta }_z∥\sigma {\mathrm{\Psi }}_z∥-∥\sigma {\mathrm{\Psi }}_r∥-{\eta }_z{E}_0∥\sigma ∥=0.$$

(14)

4.

The interfacial condition for the mass transfer across the interface, that is, the kinematic condition, is provided by [14,15].

$$m{\eta }_t∥\rho ∥+{\eta }_z∥\rho ({\mathrm{\Phi }}_z+\mathbf{U})∥-∥\rho {\mathrm{\Phi }}_r∥=0$$

(15)

5.

The conservation of energy transfer condition [14,15] is:

$${\rho }_1\left[{\mathrm{\Phi }}_{1r}-m{\eta }_t-{\eta }_z({\mathrm{\Phi }}_{1z}+U_1)\right]=\alpha m\eta$$

(16)

where $\alpha$ is the coefficient of heat and mass transfer

6

The remaining dynamical boundary condition regarding the mass transport across the interface, as shown by many authors [14,15], is the conservation of momentum balance:

$$∥\rho \left(\mathbf{v}.\nabla S\right)\left(\frac{\partial S}{\partial t}+\mathbf{v}.\nabla S\right)∥+\frac{1}{2}∥\epsilon \left(E_t^2-E_n^2\right)∥+∥P∥+T\nabla .\mathbf{n}=0$$

(17)

where P is the pressure and $E_t$ and $E_n$ are the tangential and normal components of the electric field, respectively. Integrating the linear equation of motion (1) results in Bernoulli’s formula; eliminating the pressure using Bernoulli equation, condition (17) can be rewritten in linearized form as

$$\begin{array}{cc}\hfill & \frac{1}{m^2}∥\rho U{\mathrm{\Phi }}_z∥+\frac{1}{m}∥\rho {\mathrm{\Phi }}_t∥+\frac{1}{{\lambda }_1}∥\rho \nu \mathrm{\Phi }∥-\frac{1}{{\lambda }_1}∥\rho {\nu }^{\prime }{\mathrm{\Phi }}_t∥+E_0∥\epsilon {\mathrm{\Psi }}_z∥\hfill \\ \hfill & +g\eta ∥\rho ∥-T({\eta }_{zz}+R^{-2}\eta )=0,\hfill \end{array}$$

(18)

3. Stability Analysis

3.1. Derivation of Characteristic Equation

Obtaining the solutions for the deformed interface $\eta (z,t)$ requires the velocity potentials ${\mathrm{\Phi }}_j(r,z,t)$ and electrostatic ptentials ${\mathrm{\Psi }}_j(r,z,t)$, as shown by many previous authors [15]. We use the well-known normal mode technique. Hence, all previous quantities will henceforth take the form

$$f\left(r\right).expi(kz-\omega t),$$

(19)

where $f\left(r\right)$ is a function of r, k is the wavenumber component along the z-direction, $\omega$ denotes the complex growth rate, and $i=\sqrt{-1}$ is the imaginary unit. Here, we can use Equation (19) together with Equations (3), (4), (9), and (10) along with the suitable boundary conditions (11)–(16) to represent the first order solutions of the potential functions as

$$\eta =A.expi(kz-\omega t).$$

(20)

$${\mathrm{\Phi }}_j=\pm \frac{1}{k{\rho }_j}\left[m\alpha +i(k{U}_1-m\omega ){\rho }_j\right]{\gamma }_j\left(kr\right)A.expi(kz-\omega t),j=1,2$$

(21)

$${\mathrm{\Psi }}_j=\left[\frac{i{E}_0({\sigma }_2-{\sigma }_1)}{N_j\left(kR\right)({\sigma }_1{\beta }_1\left(kR\right)+{\sigma }_2{\beta }_2\left(kR\right))}\right]N_j\left(kr\right)A.expi(kz-\omega t),j=1,2$$

(22)

where

$${\gamma }_j\left(kr\right)=\pm \frac{K_1\left(k{R}_j\right)I_0\left(kr\right)+I_1\left(k{R}_j\right)K_0\left(kr\right)}{K_1\left(k{R}_j\right)I_1\left(kR\right)-I_1\left(k{R}_j\right)K_1\left(kR\right)}$$

(23)

$${\beta }_j\left(kr\right)=\pm \frac{K_0\left(k{R}_j\right)I_1\left(kr\right)+I_0\left(k{R}_j\right)K_1\left(kr\right)}{K_0\left(k{R}_j\right)I_0\left(kR\right)-I_0\left(k{R}_j\right)K_0\left(kR\right)}$$

(24)

$$N_j\left(kr\right)=K_0\left(k{R}_j\right)I_0\left(kr\right)-I_0\left(k{R}_j\right)K_0\left(kr\right)$$

(25)

where A is the complex amplitude of the surface elevation and $I_m$ and $K_m$, ($m=0$, 1) are the modified Bessel functions of the first and second kinds, respectively. By substituting the previous solutions (20)–(22) in condition (18), the frequency $\omega$ and the wavenumber k in the view of the previous solutions for $\eta ,{\mathrm{\Phi }}_j$ and ${\mathrm{\Psi }}_j$, $(j=1,2)$ should satisfy the characteristic equation

$$\begin{array}{cc}\hfill S\left(\omega ,k\right)& =\frac{1}{m^{2}k}\left[{\rho }_1{\gamma }_1\left(kR\right){(k{U}_1-m\omega )}^2+{\rho }_2{\gamma }_2\left(kR\right){(k{U}_2-m\omega )}^2\right]\hfill \\ \hfill & +\frac{1}{{\lambda }_{1}k}\left[{\rho }_1{\nu }_1^{\prime }{\gamma }_1\left(kR\right)(k{U}_1-m\omega )+{\rho }_2{\nu }_2^{\prime }{\gamma }_2\left(kR\right)(k{U}_2-m\omega )\right]\omega \hfill \\ \hfill & -\frac{i}{{\lambda }_{1}k}\left[{\rho }_1{\nu }_1{\gamma }_1\left(kR\right)(k{U}_1-m\omega )+{\rho }_2{\nu }_2{\gamma }_2\left(kR\right)(k{U}_2-m\omega )\right]\hfill \\ \hfill & -\frac{i\alpha }{mk}\left[{\gamma }_1\left(kR\right)(k{U}_1-m\omega )+{\gamma }_2\left(kR\right)(k{U}_2-m\omega )\right]\hfill \\ \hfill & -\frac{m\alpha }{{\lambda }_{1}k}\left[\left({\nu }_1{\gamma }_1\left(kR\right)+{\nu }_2{\gamma }_2\left(kR\right)\right)+i\omega \left({\nu }_1^{\prime }{\gamma }_1\left(kR\right)+{\nu }_2^{\prime }{\gamma }_2\left(kR\right)\right)\right]\hfill \\ \hfill & -\frac{k{E}_0^2({\epsilon }_2-{\epsilon }_1)({\sigma }_2-{\sigma }_1)}{\left[{\sigma }_1{\beta }_1\left(kR\right)+{\sigma }_2{\beta }_2\left(kR\right)\right]}+\frac{T}{R^2}\left(1-k^2{R}^2\right)=0\hfill \end{array}$$

(26)

Equation (26) is simplified in the dispersion relation

$$a_0{\omega }^2+(a_1+i{b}_1)\omega +(a_2+i{b}_2)=0$$

(27)

where

$$\begin{array}{cc}\hfill a_0& =\frac{1}{k}\left[{\rho }_1{\gamma }_1\left(kR\right)+{\rho }_2{\gamma }_2\left(kR\right)-\frac{m}{{\lambda }_1}\left[{\rho }_1{\nu }_1^{\prime }{\gamma }_1\left(kR\right)+{\rho }_2{\nu }_2^{\prime }{\gamma }_2\left(kR\right)\right]\right]\hfill \\ \hfill a_1& =\frac{1}{{\lambda }_1}\left[{\rho }_1{\nu }_1^{\prime }{U}_1{\gamma }_1\left(kR\right)+{\rho }_2{\nu }_2^{\prime }{U}_2{\gamma }_2\left(kR\right)\right]-\frac{2}{m}\left[{\rho }_1{U}_1{\gamma }_1\left(kR\right)+{\rho }_2{U}_2{\gamma }_2\left(kR\right)\right]\hfill \\ \hfill b_1& =\frac{\alpha }{k}\left[{\gamma }_1\left(kR\right)+{\gamma }_2\left(kR\right)\right]+\frac{m}{{\lambda }_{1}k}\left[{\rho }_1{\nu }_1{\gamma }_1\left(kR\right)+{\rho }_2{\nu }_2{\gamma }_2\left(kR\right)\right]\hfill \\ \hfill & -\frac{m\alpha }{{\lambda }_{1}k}\left[{\nu }_1^{\prime }{\gamma }_1\left(kR\right)+{\nu }_2^{\prime }{\gamma }_2\left(kR\right)\right]\hfill \\ \hfill a_2& =\frac{k}{m^2}\left[{\rho }_1{U}_1^2{\gamma }_1\left(kR\right)+{\rho }_2{U}_2^2{\gamma }_2\left(kR\right)\right]-\frac{m\alpha }{{\lambda }_{1}k}\left[{\nu }_1{\gamma }_1\left(kR\right)+{\nu }_2{\gamma }_2\left(kR\right)\right]\hfill \\ \hfill & -\frac{k{E}_0^2({\epsilon }_2-{\epsilon }_1)({\sigma }_2-{\sigma }_1)}{\left[{\sigma }_1{\beta }_1\left(kR\right)+{\sigma }_2{\beta }_2\left(kR\right)\right]}+\frac{T}{R^2}\left(1-k^2{R}^2\right)\hfill \\ \hfill b_2& =-\frac{\alpha }{m}\left[U_1{\gamma }_1\left(kR\right)+U_2{\gamma }_2\left(kR\right)\right]-\frac{1}{{\lambda }_1}\left[{\rho }_1{\nu }_1{U}_1{\gamma }_1\left(kR\right)+{\rho }_2{\nu }_2{U}_2{\gamma }_2\left(kR\right)\right]\hfill \end{array}$$

(28)

In addition, we consider the following three special cases.

• In the presence of heat and mass transfer $\alpha$, inviscid Kelvin–Helmholtz instability, i.e., (${\nu }_1={\nu }_2=0$), pure flow with no elasticity, i.e., (${\nu }_1^{\prime }={\nu }_2^{\prime }=0$), non porous medium, i.e., ($m=1$), and absence of applied electric field ($E_0=0$), the dispersion relation (27) reduces to the same equation as established by Nayak and Chakraborty [33].
• In the presence of an applied electric field ($E_0)$ without heat and mass transfer, i.e., ($\alpha =0)$, inviscid Rayleigh–Taylor instability, i.e., ($U_1=U_2=0$), pure flow with no elasticity, i.e., (${\nu }_1^{\prime }={\nu }_2^{\prime }=0$), and a non-porous medium, i.e., ($m=1$), relation (27) reduces to the same equation as was derived by Elhefnawy et al. [29].
• Finally, in a case with inviscid Rayleigh–Taylor instability, the absence of an electric field, porosity, and heat and mass transfer for a pure hydrodynamic jet, Equation (27) reduces to the same relation first presented by Rayleigh [54].

3.2. Growth Rate and Stability Criteria

Let $\omega ={\omega }_r+i{\omega }_i$; then, separating Equation (27) into real and imaginary components, we have

$$a_0({\omega }_r^2-{\omega }_i^2)+(a_1{\omega }_r-b_1{\omega }_i)+a_2=0$$

(29)

and

$${\omega }_r=-\frac{\left(a_1{\omega }_i+b_2\right)}{2(a_0{\omega }_i+b_1)}$$

(30)

Eliminating ${\omega }_r$ between (29) and (30), we obtain

$$c_4{\omega }_i^4+c_3{\omega }_i^3+c_2{\omega }_i^2+c_1{\omega }_i+c_0=0$$

(31)

where

$$\begin{array}{cc}\hfill c_0& =a_2{b}_1^2-a_1{b}_1{b}_2+a_0{b}_2^2\hfill \\ \hfill c_1& =4a_0{a}_2{b}_1-b_1^3-a_1^2{b}_1\hfill \\ \hfill c_2& =4a_0^2{a}_2-5a_0{b}_1^2-a_0{a}_1^2\hfill \\ \hfill c_3& =-8a_0^2{b}_1\hfill \\ \hfill c_4& =-4a_0^3\hfill \end{array}$$

(32)

The maximum growth rate can be obtained by solving $\partial {\omega }_i/\partial k=0$, as discussed earlier in Awasthi [55]. Neutral curves are obtained by using ${\omega }_i\left(k\right)=0$ in (31); then, we obtain the neutral state by $c_0=0.$ Here, we can apply the Routh–Hurwitz stability criterion [56] to the dispersion relation (27); then, the structure will be linearly stable according to

$$b_1>0$$

(33)

and

$$a_2{b}_1^2-a_1{b}_1{b}_2+a_0{b}_2^2\le 0,$$

(34)

Therefore, the structure will be stable if conditions (33) and (34) are simultaneously satisfied; otherwise, it will be unstable. It is worth noting that if no kinematic viscosity or kinematic viscoelasticity exist, the structure’s stability will be determined solely by Equation (34). Because $b_1$ in (27) is independent of the electric field $E_0^2$ while being a necessary condition for the stability analysis, the condition (34) must be considered here. In the early calculations, which have been verified by many authors [50,51], it appears that the parameter $b_1$ is always of positive significance. The coefficient $b_1$ depends on the values of the structure parameters. Thus, we can choose the parameters $\alpha ,m,{\nu }_1,{\nu }_2,$${\nu }_1^{\prime },$ and ${\nu }_2^{\prime }$ such that the first condition $b_1>0$ is automatically achieved. Now, we examine the effect of the electric field intensity, $E_0^2$, on the structure’s stability. Therefore, the second condition (34) is written in the form

$$E_0^2\ge E_c^2$$

(35)

and

$$E_c^2=\frac{1}{B_2{b}_1^2}\left(A_2{b}_1^2-a_1{b}_1{b}_2+a_0{b}_2^2\right)$$

(36)

where

$$\begin{array}{cc}\hfill A_2& =\frac{k}{m^2}\left[{\rho }_1{U}_1^2{\gamma }_1\left(kR\right)+{\rho }_2{U}_2^2{\gamma }_2\left(kR\right)\right]-\frac{m\alpha }{{\lambda }_{1}k}\left[{\nu }_1{\gamma }_1\left(kR\right)+{\nu }_2{\gamma }_2\left(kR\right)\right]\hfill \\ \hfill & +\frac{T}{R^2}\left(1-k^2{R}^2\right)\hfill \\ \hfill B_2& =\frac{k({\epsilon }_2-{\epsilon }_1)({\sigma }_2-{\sigma }_1)}{\left[{\sigma }_1{\beta }_1\left(kR\right)+{\sigma }_2{\beta }_2\left(kR\right)\right]}\hfill \end{array}$$

(37)

4. Numerical Results and Discussion

Before proceeding with the numerical analysis of linear stability, it is useful to express the stability criteria, (33) and (34), in appropriate non-dimensional forms. This can happen in a variety of ways, mainly depending on the characteristic length, time, and mass chosen. For this, we investigate the non-dimensional forms based on the the characteristic time $1/\widehat{\omega },$ characteristic length $R,$ and characteristic mass $T/{\widehat{\omega }}^2$, where $\widehat{\omega }$ is a characteristic value of $\omega$. The remaining non-dimensional quantities can be written as

$$\begin{array}{c}k=\frac{k^{\ast }}{R},\rho ={\rho }^{\ast }\frac{T}{R^3{\widehat{\omega }}^2},U=U^{\ast }\widehat{\omega }R,E_0^2=E_0^{2\ast }\frac{T}{R},\hfill \\ \nu ={\nu }^{\ast }\frac{T}{R^3\widehat{\omega }},\alpha ={\alpha }^{\ast }\frac{T}{R^3\widehat{\omega }},r=r^{\ast }R,{\lambda }_1={\lambda }_1^{\ast }{R}^2,\omega =\widehat{\omega }{\omega }^{\ast }\hfill \end{array}$$

(38)

The superscript asterisks refer to non-dimensionl quantities, and are omitted for simplicity. As mentioned above, we focus on the effect of the electric field intensity on the structure of cylindrical fluids. In addition, the domain of the parameters that satisfies condition (33) is considered. The next step is to investigate the structure’s stability; keeping in mind the considered non-dimensional procedure, we can draw two groups of figures. The first group is obtained using Equation (36) to illustrate the behavior of the electric field intensity $log{E}_0^2$ against the wavennumber k for different values of the parameters included in the study. The second group of figures is obtained by using Equation (31) to clarify the variation of the growth rate ${\omega }_i$ with the wavennumber k for different values of the other physical parameters.

In the first group of figures, we carry out a numerical analysis in order to determine the structure’s stability by plotting the neutral curves described by Equation (36) in the $log{E}_0^2-k$ plane when $E_0^2=E_c^2$. The upper stable regions, S, are separated from the lower unstable ones, U, by these curves. These transition curves are plotted for a structure having ${\rho }_1=0.9$, ${\rho }_2=0.2$, ${\epsilon }_1=1.5$, ${\epsilon }_2=0.7$, ${\nu }_1=0.8$, ${\nu }_2=0.9,$${\sigma }_1=0.6$, ${\sigma }_2=0.1$, ${\nu }_1^{\prime }=0.5,$${\nu }_2^{\prime }=$$0.6,$$R_1=0.1,R=0.2,$$R_2=0.3$, $U_1=1$, $U_2=10$, $\alpha =0.5,m=0.05,$ and ${\lambda }_1=0.5$. In Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, the first dimension represents the wave number, k, and the second represents the electric field, $log{E}_0^2$, with the latter one of the previous parameters.

Figure 2 and Figure 3 introduce a detailed discussion for the influence of the electrical conductivities ${\sigma }_1$, ${\sigma }_2$ on the stability of the fluid cylindrical structure. Figure 2 shows the variation of the electric field $log{E}_0^2$ versus k for the different electrical conductivity values ${\sigma }_1$(${\sigma }_1>$${\sigma }_2$), with ${\sigma }_2$ fixed (${\sigma }_2=0.1$). It can be seen that when the inner fluid conductivity is increased from ${\sigma }_1=0.2$ to ${\sigma }_1=0.25$ and then to ${\sigma }_1=10,$ the instability region U increaseds for a small wavenumber range ($k\le 2.5$), after which the stability does not depend on ${\sigma }_1$, as the curves are coincident. Then, the increase of the inner fluid conductivity ${\sigma }_1$ with fixed outer fluid conductivity ${\sigma }_2$ increases the instability of the structure, which shows the destabilizing effect of the inner fluid conductivity, ${\sigma }_1$, on the structure. It should be noted that the effect of the electrical conductivity values ${\sigma }_2$(${\sigma }_2>$ ${\sigma }_1$), with ${\sigma }_1$ fixed (${\sigma }_1=0.1$) on the stability of the structure, are found to be opposite to the effect of the previous case shown in Figure 2. While the figure is not shown here to save space, it indicates that the increase in the outer fluid conductivity, ${\sigma }_2$, with fixed inner fluid conductivity ${\sigma }_1$ increases the stability of the structure, which shows the stabilizing effect of the outer fluid conductivity ${\sigma }_2$ on the structure. On the other hand, Figure 3 shows the the influence of increasing the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_1>$ ${\sigma }_2$); it can be seen that by increasing ${\sigma }_1,{\sigma }_2$, the stability region S increases for a small wavenumber range ($k\le 2.5$), which shows the stabilizing effect of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_1>$ ${\sigma }_2$) on the considered structure. It should be noted that the effect of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_2>$ ${\sigma }_1$) on the stability of the structure is opposite to the effect of the previous case shown in Figure 3. While the figure is not shown here in order to save space, it indicates that an increase in the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_2>$ ${\sigma }_1$) increases the instability of the structure, showing the destabilizing effect of electrical conductivity values ${\sigma }_1,{\sigma }_2.$ Hence, we conclude that electrical conductivity has a dual role on the stability of the cylindrical structure, which is in agreement with the previous results acheived by Elhefnawy [30] and Elsayed [36].

Figure 4, Figure 5 and Figure 6 show the variations of the electric field $log{E}_0^2$ with the wavenumber k for various values of the kinematic viscosities ${\nu }_1$, ${\nu }_2,$ (${\nu }_2>{\nu }_1$), the kinematic viscoelasticities ${\nu }_1^{\prime },{\nu }_2^{\prime },$ (${\nu }_2^{\prime }>{\nu }_1^{\prime }$), and the porosity of the medium m, respectively. It is shown that by increasing the parameter values for each of ${\nu }_1$, ${\nu }_2,$ (${\nu }_2>{\nu }_1)$ in Figure 4, ${\nu }_1^{\prime },{\nu }_2^{\prime },$ (${\nu }_2^{\prime }>{\nu }_1^{\prime })$ in Figure 5, and the porosity value m in Figure 6, respectively, the stability region S in Figure 4, Figure 5 and Figure 6 increases. Thus, we can conclude that each of the kinematic viscosities ${\nu }_1$, ${\nu }_2,$ (${\nu }_2>{\nu }_1),$ kinematic viscoelasticities ${\nu }_1^{\prime },{\nu }_2^{\prime },$ (${\nu }_2^{\prime }>{\nu }_1^{\prime })$, and the porosity of the medium m, has stabilizing effects on the stability of the structure. These results are in agreement with previous results for two semi-infinite viscoelastic dielectric fluids acheived by El-Sayed [50].

By contrast, Figure 7, Figure 8 and Figure 9 show the variations of the electric field $log{E}_0^2$ with the wavenumber k for various values of the fluid velocities $U_1$, $U_2$, ($U_2$$>U_1),$ the mass and heat transfer coefficient values $\alpha$, and the permeability of the medium ${\lambda }_1$, respectively. It can be seen that by increasing the parameter values for each of the fluid velocities $U_1$, $U_2$, ($U_2$$>U_1)$ in Figure 7, the mass and heat transfer coefficient values $\alpha$ in Figure 8 and the permeability of the medium ${\lambda }_1$ in Figure 9, respectively, the instability region U in Figure 7, Figure 8 and Figure 9 has increased. Hence, we can conclude that each of the fluid velocities $U_1$, $U_2$, ($U_2$$>U_1),$ the mass and heat transfer coefficient values $\alpha$, and the permeability of the medium ${\lambda }_1$, respectively, have destabilizing effects on the stability of the structure. These results are in agreement with the previous results obtained by Elhefnawy [30] and Moatimid [52,53].

In the second group of figures, we investigated the influence of various physical elements included in the analysis of growth rate instability. We utilized Mathematica Software to perform numerical calculations of the dispersion relation (31) in order to determine the roots of the growth rate ${\omega }_i$ versus the wavenumber k. These computations are depicted in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, illustrating the variation of the growth rate ${\omega }_i$ with the wavenumber k for different values of the investigated structural characteristics. Figure 10, Figure 11 and Figure 12 show the variations of the imaginary growth rate ${\omega }_i$ with the wavenumber k for different values of the fluid velocities $U_1$, $U_2$, ($U_2$$>U_1)$, the permeability of the medium ${\lambda }_1$, and the mass and heat transfer coefficient values $\alpha$, respectively. It is obvious from these figures that the growth rate, ${\omega }_i$, increases with increasing k until a maximum growth rate is reached at a critical wavenumber value, after which ${\omega }_i$ decreases, as seen in Figure 10, Figure 11 and Figure 12, respectively. By increasing the values of the fluid velocities $U_1$, $U_2$, ($U_2$$>U_1)$, the permeability of the medium ${\lambda }_1$, and the mass and heat transfer coefficient values $\alpha$, the maximum imaginary part of the growth rate ${\omega }_i$ increases when increasing the values of $U_1$, $U_2$, ${\lambda }_1$, and $\alpha$ in the wavenumber ranges, showing the destabilizing effects of these parameters on the stability of the structure. It is clear from these figures that the instability arising due to the effect of the fluid velocities $U_1$, $U_2$ is stronger than the instability arising due to the permeability of the medium ${\lambda }_1$, and the later one is in turn stronger than the effect of the mass and heat transfer coefficient values $\alpha$.

Figure 13 and Figure 14 show the variations in the imaginary part of the growt rate ${\omega }_i$ against the wavenumber k for different values of the kinematic viscosities ${\nu }_1$, ${\nu }_2,$ (${\nu }_2>{\nu }_1),$ and kinematic viscoelasticities ${\nu }_1^{\prime },{\nu }_2^{\prime },$ (${\nu }_2^{\prime }>{\nu }_1^{\prime })$, respectively. It is clear from these figures that the kinematic viscosities ${\nu }_1$, ${\nu }_2$ and kinematic viscoelasticities ${\nu }_1^{\prime },{\nu }_2^{\prime }$ have no effect on the stability of the structure for the small wavenumber range k < 0.06, because the imaginary part of growth rate ${\omega }_i$ curves are coincident for different values of ${\nu }_1$, ${\nu }_2$ and ${\nu }_1^{\prime },{\nu }_2^{\prime }$. In addition, we note that ${\omega }_i$ increases with increasing k until a maximum growth rate of ${\omega }_i$ is reached at a critical wavenumber value, after which ${\omega }_i$ decreases, as can be seen in Figure 13 and Figure 14. By increasing the values of the parameters ${\nu }_1$, ${\nu }_2,$ (${\nu }_2>{\nu }_1)$ and ${\nu }_1^{\prime },{\nu }_2^{\prime },$ (${\nu }_2^{\prime }>{\nu }_1^{\prime })$, we found that the maximum imaginary part of the growth rate ${\omega }_i$ decreases by increasing their values in the same wavenumber range, showing the stabilizing effects of these parameters on the considered structure. Figure 15, Figure 16 and Figure 17 show the variations in the imaginary part of the growth rate ${\omega }_i$ with the wavenumber k for the different values of electrical conductivity ${\sigma }_1$, ${\sigma }_2$, (${\sigma }_1>$${\sigma }_2)$, the axial electric field $E_0$, and the porosity of the medium m, respectively. It is clear from these figures that for the small wavenumber range k < 0.06, both of electrical conductivites values ${\sigma }_1$, ${\sigma }_2$, (${\sigma }_1>$${\sigma }_2)$ and the axial electric field $E_0$ have no effect on the stability of the structure, as the imaginary part of the growth rate ${\omega }_i$ curves are coincident for the different values of the electrical conductivity values ${\sigma }_1$, ${\sigma }_2$, (${\sigma }_1>$${\sigma }_2)$ and axial electric field $E_0$ in Figure 15 and Figure 16. In addition, for any value of ${\sigma }_1$, ${\sigma }_2$ or $E_0$, or m, we note that ${\omega }_i$ increases with increasing k until a maximum growth rate at a critical wavenumber value, after which ${\omega }_i$ decreases, as can be seen in Figure 15, Figure 16 and Figure 17. By increasing the values of the parameters ${\sigma }_1$, ${\sigma }_2$, (${\sigma }_1>$${\sigma }_2)$, $E_0$ and m, we found that the maximum imaginary part of growth rate ${\omega }_i$ decreases when increasing their values in the same wavenumber range, showing the stabilizing effects of the parameters ${\sigma }_1$, ${\sigma }_2$, (${\sigma }_1>$${\sigma }_2)$, $E_0$ and m on the considered structure. Finally, It is obvious from Figure 15, Figure 16 and Figure 17 that the stability arises due to the effect of the electrical conductivity values ${\sigma }_1$, ${\sigma }_2$ takes hold faster than the stability arises due to the effect of the electric field $E_0$, and the latter takes hold faster than the stability rises due to the effect of the porosity of the medium m. It should be noted that the effects of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_2>$${\sigma }_1$) and the axial electric field $E_0$(${\sigma }_2>$ ${\sigma }_1$) on the stability of the structure are opposite to the effect of the previous cases shown in Figure 15 and Figure 16; however, these figures are not shown here in order to save space. They indicate that the increase of electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_2>$${\sigma }_1$) increase the instability of the structure, which shows the destabilizing effect of the electrical conductivity values ${\sigma }_1{\sigma }_2({\sigma }_2>{\sigma }_1)$ and the axial electric field $E_0$(${\sigma }_2>$ ${\sigma }_1$). Thus, we conclude that electrical conductivity has a dual role in the stability of the cylindrical structure, which is in agreement with previous results.

5. Conclusions

In this article, novel results for Walters B viscoelastic fluid flows through a cylindrical structure in a porous medium are provided and investigated for weakly electrically conducting fluids. Accurate analytical solutions are presented for all parameters. A series of parametric analyses were used to study the relationship between electrical forces, viscoelastic stresses, and hydrodynamic interaction. Using the usual normal mode procedure, a second-order dispersion equation of complex coefficients characterizing the behavior of the perturbed structure was obtained and stability discussion was carried out via the critical value of the applied electric field of the two fluids, along with the imaginary part of the growth rate. The obtained results are outlined as follows:

• The electrical conductivities ${\sigma }_1,{\sigma }_2$ play a critical role in the cylindrical structure’s mechanism. The axial electric field $E_0,$ according to its value, has a dual role on the structure’s stability. From this, the following new results can be summarized.
• The increase of the inner fluid conductivity ${\sigma }_1$ with fixed outer fluid conductivity ${\sigma }_2$ increases the instability of the structure, showing the destabilizing effect of the inner fluid conductivity ${\sigma }_1$, while the increase in the outer fluid conductivity ${\sigma }_2$ with fixed inner fluid conductivity ${\sigma }_1$ decreases, showing the stabilizing effect of the outer fluid conductivity ${\sigma }_2$.
• The increase of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_1>$${\sigma }_2$) increases the stability of the structure for a small wavenumber range ($k\le 2.5$), showing the stabilizing effect of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_1>$${\sigma }_2$). The increase of the electrical conductivity values ${\sigma }_1,{\sigma }_2$(${\sigma }_2>$${\sigma }_1$) increases the instability of the structure, showing the destabilizing effect of these electrical conductivity values. These results are in agreement with the previous results achieved by Elhefnawy [30] and Elsayed [36].

  –

  The kinematic viscosities ${\nu }_1$, ${\nu }_2$, kinematic viscoelasticities ${\nu }_1^{\prime },{\nu }_2^{\prime }$, and porosity of the medium m have stabilizing effects on the structure.

  –

  The permeability of the medium ${\lambda }_1$, the mass and heat transfer coefficient $\alpha$, and the fluid velocities $U_1$, $U_2$ have destabilizing effects on the structure.

  –

  The second group of figures (${\omega }_i$, k) for different values of the parameters confirm the same results obtained in the first group of figures ($log{E}_0^2$, k); through these groups, the previous limiting case can be recovered. Nonlinear effects in EHD phenomena will be discussed in a future study.