2.1. Deriving Stage Variation–Discharge Relationship for the Non-Linear Water Reservoir
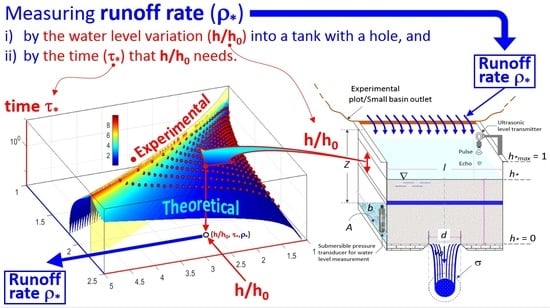
Consider an open rectangular tank, with sides
l (m) and
b (m), base area,
A (m
2), and height
Z (m), as displayed in
Figure 3. A circular sharp-crested orifice with diameter
d (m) and cross-sectional area, σ (m
2), is made at the bottom of the tank. A stationary and uniformly distributed runoff intensity,
r (m s
−1) corresponding to a runoff discharge
R (m
3 s
−1), is applied over the tank (
Figure 3).
The tank water level is denoted as
h (m) and can be measured either by a submersible pressure transducer or by an ultrasonic probe, coupled with a data logger (
Figure 3). The latter can be installed at the top of a wide piezometer connected to the water tank, in order to measure the height to which a column of the water rises against gravity, without the disturbance effects at the open water surface caused by the incoming runoff discharge into the tank.
The water level is also expressed in dimensionless terms as
h∗ =
h/
Z. Thus,
h∗ = 0 and
h∗ = 1 (
Figure 3) indicate that the water tank is completely empty or full, respectively. Furthermore, the outflow rate from the hole of the water tank is denoted as
v0 (m/s) and the corresponding discharge as
Q0 (m
3 s
−1). The one-dimensional differential continuity equation applied to the infinitesimal volume,
dh height (
Figure 3), can be written as:
where
t (s) is the time and μ is the discharge coefficient (usually assumed as 0.6 for a perfectly crested orifice) that takes into account the reduction of the discharge velocity due to the viscous behavior of the water (coefficient of velocity) and the reduction of the effective outflow cross-section due to the
vena contracta (coefficient of contraction) [
36]. Values of the discharge coefficient, μ, which slightly differ from 0.6 could also be taken into account, by considering the unified equation developed by Swamee and Swamee [
37] that provides a smooth transition between viscous and potential flows.
Equation (1) states that during a runoff event with constant discharge,
R, the water volume exiting the jet by the outlet, in time
dt, is equal to the water volume removed from the tank added to that stored in the tank, in the same time
dt. In Equation (1), the outflow rate,
v0, can be expressed by the well-known Torricelli law, which derives by the conservation of energy [
21]:
where
g (m s
−2) is the acceleration due to gravity. The water level gradient can be derived by Equation (1):
For the continuity condition of the flow,
v0 (Equation (2)) can also be expressed as a function of the outflow rate,
v, as referred to the tank base area,
A (
Figure 3):
Substituting Equation (4) into Equation (1) allows rewriting the water level rate:
Now, define a characteristic time for the emptying tank process,
tc, as the time that the water particle starting from the top water tank needs to cross the entire tank height
Z, under steady state conditions and with velocity
v =
vmax:
where
vmax is the maximum value of
v associated with
v0 (Equation (4)). Equation (6) shows that, of course,
tc also corresponds to the minimum travel time required for the water particle to cross the entire tank height.
The maximum velocity of the water tank level,
vmax, can be derived by Equation (4) and by placing
h =
Z in Equation (2):
As expected, Equations (6) and (7) show that the more
vmax increases the less the travel time,
tc, will be. Dividing the numerator and the denominator on the left side of Equation (5) by the characteristic time
tc (Equation (6)), provides:
where τ is the time normalized with respect to
tc, while
h∗ is the water level,
h, normalized with respect to the tank height,
Z. Equation (8), which is consistent in regard to a dimensional point of view, can be further simplified as:
where ρ is the runoff excess intensity,
r (m s
−1), i.e.,
R/
A, normalized with respect to
vmax:
and where √
h∗ was obtained by substituting into Equation (8) the following ratio:
Equation (9) is a more compacted form of the differential flow equation than Equation (1), and it can be usefully considered for the purposes of this study, in order to derive a purely theoretical stage–discharge relationship for measuring input runoff discharges to be directly used in field and in experimental applications, requiring limited calibration, as will be shown. Equation (8) can be integrated, by fixing the initial condition
h =
h0 for
t =
t0, or in dimensionless terms:
under the reasonable assumption that during the close interval [τ
0, τ], which could also fit the normalized time step of water level measurements (τ
m = τ − τ
0), the runoff discharge
R (Equation (1)) and the corresponding ρ are time-invariant:
Equation (13) shows that for ρ = √h∗ a limiting condition occurs, so that the normalized water content asymptotically attains an equilibrium value, which can be derived by imposing h∗ = ρ2.
Two different cases can be distinguished:
(i) ρ ≠ 0. In this case, the integral of Equation (13) can be solved by
u-substitution or the reverse chain rule, by putting
u = √
h∗ and
dh∗ = 2
u du, giving:
Adding and subtracting ρ in the numerator yields:
By substituting back again into Equation (15)
u = √
h∗, an explicit τ solution can be derived:
(ii) ρ = 0. This case describes the recession of the emptying tank process, starting at the end of the runoff process, τ
r, i.e., τ
0 = τ
r and
h*0 =
h*r, with
h*r denoting the normalized water level at the end of the runoff process, when ρ = 0. Thus, Equation (13) can be rewritten as:
which, once integrated, provides the following explicit solution in τ or in
h∗, respectively:
According to the dimensionless variables introduced, Equation (18) makes it possible to derive the time required for the zero flux condition, τ
zf, i.e., for
h∗ = 0, when the tank is completely empty:
that can be expressed dimensionally by using Equations (6) and (7) and assuming τ
r = 0, yielding the well-known formula:
Equations (20) and (21) are not strictly useful towards the objectives of this work since they can be applied at the end of the runoff process, when the runoff intensity, r, equals zero. However, they can be used to test how well the runoff measurement device performs, since it makes it possible to check that when the water level is h = h∗ = 0, the time that passes from the initial water level, i.e., hr, to the zero flux condition would be tzf = τzf tc.
It should be noted that Equation (9) differs from the well-known linear reservoir model, commonly used in catchment hydrology, which assimilates the catchment to a reservoir. In fact, in that case, it is assumed that the water volume stored in the reservoir linearly varies with the output discharge, according to a constant
k(
t), which is also related to the response time of the catchment [
38,
39]. This assumption would provide a different form of the differential equation and its solution, which are reported in a dimensional form here, by assuming as initial condition
v = 0, for
t = 0:
The linearity assumption in Equations (22) and (23) is an approximation. This is equivalent to assuming that the superposition principle could be applied to both the runoff generation process in the catchment hydrology, and to the water tank behavior, if referring to this study. Actually, both the runoff generation process, especially at the hillslope scale [
40,
41], and the water reservoir (the latter because of introducing Torricelli’s law), are non-linear. Therefore, in both cases, the superposition principle is not satisfied and thus cannot be applied. With reference to the non-linear water tank considered in this study, by using the Laplace transform, Equation (9) could be linearized; however, this issue is beyond the objective of this work and does not further contribute to the results that will be shown.
In order to derive the normalized runoff discharge, ρ, i.e., the runoff intensity (Equation (10)), Equation (16) needs to be rewritten as follows:
that provides an implicit ρ solution for a fixed normalized time τ
m spent from the initial condition
h*0 to the actual condition
h∗. Thus, the time
tm = (
t −
t0) = τ
m tc represents the time step of water level measurements, i.e., the time that the water level
h0, at
t =
t0, needs to achieve the current value
h, at
t =
t0 +
tm. Of course,
tm, i.e., τ
m, needs to be established according to the desired resolution of the indirect water level measurement device (
Figure 3).
Equation (24) shows that the output variable ρ, depends on three parameters τ
m,
h∗, and
h*0, which complicate a graphical illustration of the non-linear water tank performance. However, in Equation (24), the ρ dependence can be reduced to two parameters by dividing the left and right side by √
h*0:
By introducing the following three dimensionless groups:
Equation (25) can be rewritten, showing a ρ∗ dependence on only two dimensionless groups,
H∗ and τ∗:
thus making a better graphical parametrization than Equation (24) possible. It should also be noted that Equation (29) differs from the stage–discharge relationships mentioned in the introduction section, where relationships between water level and runoff discharge were found. Indeed, in Equation (29) no calibration coefficients appear, and the runoff discharge is related to the water level variation,
H∗, rather than the water level. Therefore, it could be more appropriate denoting Equation (29) as a stage variation–discharge relationship, as in this subsection title.
The present approach is similar to that recently applied to the soil [
42], which was also treated as a non-linear reservoir in order to derive an analytical solution for the Richards equation, under gravity-driven infiltration and constant rainfall intensity. Here, such a similar approach has been reformulated, according to a different characteristic time of the water tank and to different input and output dimensionless groups. In fact, for the soil, the known input was the rainfall intensity and the soil water content, miming the water tank level, needed to be determined; whereas in the present methodology, the input is the water level variation, and the output (i.e., the unknown) is the runoff input discharge at the outlet.
2.2. Range of Values of the Involved Parameters and Stage–Discharge Plot
In order to set a reliable range of variability of the involved dimensionless groups
H∗, ρ∗, and τ∗,
Table 1 and
Table 2 report examples of the ranges of variability of the geometric and hydraulic original variables, respectively, by fixing their assumed extremes (see min and max values). Of course, the lower the range of the input discharge, the cheaper the tank size and cost will be.
For example, a high value of the maximum height
Z of the tank was fixed (
Z = 4 m). This could make measuring runoff costly, because of the high excavation costs and the large size of the water tank. However, it would be reliable once installed downstream from a check dam where a drop in elevation occurs or more properly at the experimental plots’ outlet (
Figure 1).
Table 1 shows that the outlet hole diameter also varied in a wide range (0.02–0.3 m), in order to extend the range of variability of runoff measurements.
Once the range of variability of the involved original variables was established, those of the corresponding output dimensionless groups were determined and reported in
Table 3, which also includes those rounded ranges considered in the application of Equation (29).
According to these rounded ranges (
Table 3) and by using Equation (29), the output variable, ρ∗, which makes it possible to estimate the runoff intensity, was plotted in
Figure 4, versus
H∗, with τ∗ as a parameter, which also varied according to its range of variability (
Table 3).
Figure 4 shows that all of the curves pass from
H∗ = ρ∗ = 1, according to the fact that when no difference between
h*0 and
h∗ is measured (
H∗ = 1), the outlet process is steady state and the corresponding runoff intensity can be calculated by the well-known equation,
r = μ σ/
A √(2
g h0). Thus, under this condition, ρ∗ equals the unity (Equations (10) and (26)).
Figure 4 also shows that for any τ∗, the ρ∗(
H∗) curves monotonically increase, indicating, as expected, that for a fixed time step measurement,
tm, i.e., τ∗, at increasing
H∗ the runoff intensity also increases. Moreover, for a fixed
H∗, (i.e., for a fixed antecedent and actual water levels), runoff intensity becomes higher and higher, as the time step measurement, τ∗, decreases. This latter behavior also agrees with what is expected.
It should be noted that the tank design has to be performed according to the runoff regime of the studied plot/basin. In fact, as previously observed, tank volumes and hole diameters that are too small would not make it possible to measure the runoff intensity by the water level ratio,
H∗, since the tank would get full too quickly. On the contrary, tank volumes and hole diameters that are too large would not make it possible to measure the runoff intensity by Equation (29), because the variation of the water level ratio,
H∗, would be too small. These two latter extreme behaviors are described in
Figure 4, by the vertical and almost horizontal branches of the plotted curves, respectively.
2.3. Water Reservoir Design
Some considerations can help detect the optimal water tank design according to the suggested procedure, for different runoff regimes. In fact, for an assigned tank dimension, it is easy to derive the minimum and maximum runoff rate, and the derived relationships that can be used in regard to the tank design. In particular, the maximum outlet discharge from the tank hole,
Q0,max, and the maximum storage discharge,
Q0,st, and their sum,
Rmax, can respectively be expressed as:
whereas, by assuming a minimum water level equal to a very low fraction of
Z, α
Z, with α = 1%–2%, the corresponding minimum values,
Q0,min,
Qst,min, and
Rmin, can be derived:
By using Equations (32) and (35), and by imposing the time step measurement,
tm, derived from them as equal, the following relationship of the outlet cross-sectional area, σ, can be obtained:
Equation (36) can also be rewritten by considering the much more useful hole diameter,
d (mm), rather than the hole cross-sectional area, σ:
Table 4 reports the minimum and maximum values of the runoff discharge,
Rmax and
Rmin, respectively, for three considered study cases, run #1, run #2, and run #3, within which the runoff discharge must be measured according to its temporal variability.
For these
Rmax and
Rmin values, and by assuming a fraction of the tank height α = 0.01,
Figure 5 graphs the hole’s cross sectional area, σ, and the corresponding hole diameter,
d, according to Equation (36) (
Figure 5a) and Equation (37) (
Figure 5b), respectively.
Figure 5 shows that a water tank satisfying the
R range of variability can be designed by a multitude of pairs (
d,
Z). However, most of their values are out of the reasonable assumed ranges and can correspond to time step water level measurements,
tm, which do not necessarily match those that can be assumed in practice. In the following section, applications of the suggested procedure to measure the runoff discharge are performed and
tm values for the three runs are first calculated.