A Generalized State-Space Aeroservoelastic Model Based on Tangential Interpolation
Abstract
:1. Introduction
- There is no need for poles selection (lag states). On the one hand, the classical selection of real poles for the RFA techniques does not allow for describing phenomena which present resonance behaviour or peaks in the frequency-domain description at frequencies higher than zero. On the other hand, the set of real poles causes the RFA least-squares fit to be ill-conditioned, and care must be taken when increasing the number of poles. To overcome these limitations, within the present approach, neither a pole selection is required nor the transfer function is limited to a set of rational functions with real poles (see Section 3.1).
- It provides a small-size generalized state-space representation. The term generalized refers here to the fact that the theory of linear descriptor systems is needed for the present approach (see Section 2.1). This term should not be confused with the term generalized of the aeroelastic equation, where the physical equation is projected onto the set of generalized coordinates corresponding to the modes of the structure in vacuum. The proposed approach can be a regarded as providing a reduced order model (ROM) in the time domain, as it enables solving the aeroservoelastic system in a very efficient way. This is achieved by the condition of minimality of the rational interpolant within the Loewner framework theory [25].
- It is applicable to (input) delay systems, in particular when the excitation is due to gust disturbances. As described above, RFA techniques based on a least-squares fit of the frequency-domain data are not suited for a gust disturbance input. Two practical solutions in order to avoid this limitation of the RFA techniques, namely dividing the gust excitation in zones or applying a least-squares fit to the distributed aerodynamic nodal loads, may dramatically increase the size of the aeroelastic model in the time domain.
- It includes rigid-body modes, explicitly dealing with the singularity caused by the translational aircraft motion at zero frequency. This problem has been considered by Karpel et al. [26] in the frequency domain. In this work, the aerodynamic transfer function matrix is modified to include the derivatives of the translational motion previous to the time-domain realization.
- It is computationally efficient when generating the state-space. Unlike classical approaches where the precision is increased at the cost of an iterative approach [14], the current approach does not require any iterative process. In addition, the computational effort is drastically reduced compared to the ERA method by the consideration of tangential interpolation data within the Loewner pencil [25], avoiding the use of the dense and large-size Hankel matrix.
- It recovers the cut loads by means of the FSM. In order to achieve this, the unsteady aerodynamic loads distribution over the aircraft must be represented in the time domain. As described above, the FSM method is known to have a superior convergence for the cut loads prediction compared to the MDM method commonly used in applications for gust load alleviation (GLA) design [27].
2. Generalized Realization Problem
2.1. Tangential Interpolation
2.2. Optimal Approximation
2.3. Application to Unsteady Incompressible Flow
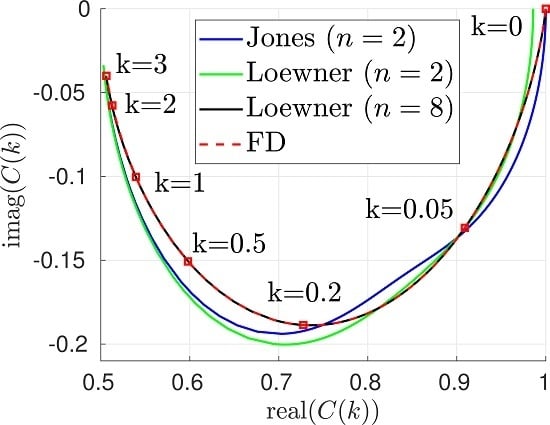
Application to the Theodorsen Function
3. Aeroservoelastic System for Loads Analysis
3.1. Generalized Realization of the Aerodynamic System
3.2. Aeroservoelastic System
- Mode displacement method (MDM), where the cut loads are given by:where the matrix corresponds to the physical stiffness matrix, includes the columns corresponding to the flexible modes and their generalized coordinates. The matrix is a summation matrix which considers the nodal loads adding up to a particular location in order to obtain the resulting (incremental with respect to a steady-state reference) cut loads such as the shear forces together with the bending and torsional moments.
- Force summation method (FSM), where the cut loads are recovered by the equilibrium of forces:where the matrix represents the physical mass matrix. For the FSM method, not only the generalized aerodynamic forces but also the aerodynamic distribution is required.
4. Application to the FERMAT Configuration
4.1. Open Loop
4.2. Closed Loop
5. Conclusions
- Different GLA control law strategies. Within the presented method, the complete aerodynamic distribution together with the cut loads and combinations thereof can be chosen as objective functions.
- Consideration of different aerodynamic theories in the frequency domain which are appropriate for the transonic flow, such as the correction of the AIC matrices or linearized CFD solvers in the frequency domain. In particular, the piston theory as limit of the DLM method for high reduced frequency values may also be considered. In this case, the residualization could be eliminated by substracting the values predicted by the piston theory from the aerodynamic transfer function matrix.
- Inclusion of parametric generalized state-space aeroservoelastic models as an alternative to the classical gain scheduling approach.
- Extension to a nonlinear generalized state-space formulation for nonlinear aeroservoelastic systems. In this case, the Loewner framework in connection with a functional or Volterra series expansion theory can be followed.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Theodorsen Function Realization
References
- European Aviation Safety Agency. Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes; Technical Report CS-25, Amendment 16; European Aviation Safety Agency: Cologne, Germany, 2015. [Google Scholar]
- Federal Aviation Regulations Part 25: Airworthiness Standards: Transport Category Airplanes. Web Resource for Research. 2015. Available online: http://www.risingup.com/fars/info/25-index.shtml (accessed on 15 March 2012).
- Eversman, W.; Tewari, A. Consistent rational-function approximation for unsteady aerodynamics. J. Aircr. 1991, 28, 545–552. [Google Scholar] [CrossRef]
- Roger, K.L. Airplane Math Modeling Methods for Active Control Design. In Proceedings of the 44th AGARD Structures and Material Panel (AGARD-CP-228), Lisbon, Portugal, 21 April 1977. [Google Scholar]
- Abel, I. An Analytical Technique for Predicting the Characteristics of a Flexible Wing Equipped with an Active Flutter-Suppression System and Comparison with Wind-Tunnel Data; Technical Report, NASA Technical Paper 1367; NASA Langley Research Center: Hampton, VA, USA, 1979.
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. A robust approach for system identification in the frequency domain. IEEE Trans. Power Deliv. 2004, 19, 1167–1173. [Google Scholar] [CrossRef]
- Karpel, M.; Moulin, B.; Chen, P. Dynamic response of aeroservoelastic systems to gust excitation. J. Aircr. 2005, 42, 1264–1272. [Google Scholar] [CrossRef]
- Mor, M.; Livne, E. Sensitivities and approximations for aeroservoelastic shape optimization with gust response constraints. J. Aircr. 2006, 43, 1516–1527. [Google Scholar] [CrossRef]
- Pusch, M.; Knoblach, A.; Kier, T. Integrated optimization of ailerons for active gust load alleviation. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD), St. Petersburg, Russia, 28 June–2 July 2015. [Google Scholar]
- Castrichini, A.; Cooper, J.; Benoit, T.; Lemmens, Y. Gust and Ground Loads Integration for Aircraft Landing Loads Prediction. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Dunn, H. An Analytical Technique for Approximating Unsteady Aerodynamics in the Time Domain; Technical Report, NASA Technical Paper 1738; NASA Langley Research Center: Hampton, VA, USA, 1980.
- Tiffany, S.; Adams, W., Jr. Nonlinear programming extensions to rational function approximations of unsteady aerodynamics. In Proceedings of the 28th Structures, Structural Dynamics and Materials Conference, Monterey, CA, USA, 6–8 April 1987. [Google Scholar]
- Karpel, M. Design for Active Flutter Suppression and Gust Alleviation Using State-Space Aeroelastic Modeling. J. Aircr. 1982, 19, 221–227. [Google Scholar] [CrossRef]
- Pototzky, A.; Perry, B., III. New and existing techniques for dynamic loads analyses of flexible airplanes. J. Aircr. 1986, 23, 340–347. [Google Scholar] [CrossRef]
- Karpel, M.; Presente, E. Structural dynamic loads in response to impulsive excitation. J. Aircr. 1995, 32, 853–861. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Cooper, J. LQG based model predictive control for gust load alleviation. Aerosp. Sci. Technol. 2017, 71, 499–509. [Google Scholar] [CrossRef]
- Juang, J.; Pappa, R. An Eigensystem Realization Algorithm for Modal Parameter Identification and Model Reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Silva, W.; Bartels, R. Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code. J. Fluids Struct. 2004, 19, 729–745. [Google Scholar] [CrossRef]
- Gaitonde, A.; Jones, D. Reduced order state-space models from the pulse responses of a linearized CFD scheme. Int. J. Numer. Methods Fluids 2003, 42, 581–606. [Google Scholar] [CrossRef]
- Ma, Z.; Ahuja, S.; Rowley, C. Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 2011, 25, 233–247. [Google Scholar] [CrossRef]
- Rowley, C. Model reduction for fluids using balanced proper orthogonal decomposition. Int. J. Bifurc. Chaos 2005, 15, 997–1013. [Google Scholar] [CrossRef]
- Kramer, B.; Gugercin, S. Tangential interpolation-based eigensystem realization algorithm for MIMO systems. Math. Comput. Model. Dyn. Syst. 2016, 22, 282–306. [Google Scholar] [CrossRef]
- Antoulas, A. Approximation of Large-Scale Dynamical Systems; SIAM: Philadelphia, PA, USA, 2005; Volume 6. [Google Scholar]
- Mayo, A.; Antoulas, A. A framework for the solution of the generalized realization problem. Linear Algebra Its Appl. 2007, 425, 634–662. [Google Scholar] [CrossRef] [Green Version]
- Karpel, M.; Shousterman, A.; Mindelis, Y. Rigid-Body Issues in FFT-Based Dynamic Loads Analysis with Aeroservoelastic Nonlinearities. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Moulin, B.; Karpel, M. Gust Loads Alleviation Using Special Control Surfaces. J. Aircr. 2007, 44, 17–25. [Google Scholar] [CrossRef]
- Sokolov, V. Contributions to the Minimal Realization Problem for Descriptor Systems. Ph.D. Thesis, Technical University Chemnitz, Chemnitz, Germany, 2006. [Google Scholar]
- Lefteriu, S.; Antoulas, A. A new approach to modeling multiport systems from frequency-domain data. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2010, 29, 14–27. [Google Scholar] [CrossRef]
- Köhler, M. On the closest stable descriptor system in the respective spaces RH2 and RH∞. Linear Algebra Appl. 2014, 443, 34–49. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NACA Technical Report 496; National Advisory Committee for Aeronautics, Langley Aeronautical Lab.: Langley Field, VA, USA, 1935.
- Brunton, S. Unsteady Aerodynamic Models for Agile Flight at Low Reynolds Numbers. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2012. [Google Scholar]
- Peters, D. Two-dimensional incompressible unsteady airfoil theory—An overview. J. Fluids Struct. 2008, 24, 295–312. [Google Scholar] [CrossRef]
- Hodges, D.; Pierce, G. Introduction to Structural Dynamics and Aeroelasticity, 2nd ed.; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Gear, C. An introduction to numerical methods for ODEs and DAEs. In Real-Time Integration Methods for Mechanical System Simulation; Springer: Berlin/Heidelberg, Germany, 1991; pp. 115–126. [Google Scholar] [CrossRef]
- Roberts, A. Differential Algebraic Equation Solvers. 1998. Available online: https://de.mathworks.com/matlabcentral/fileexchange/28-differential-algebraic-equation-solvers (accessed on 6 April 2018).
- Petzold, L. Description of DASSL: A Differential/Algebraic System Solver; Technical Report; Sandia National Labs.: Livermore, CA, USA, 1982.
- Mazelsky, B. On the Noncirculatory Flow about a Two-Dimensional Airfoil at Subsonic Speeds. J. Aeronaut. Sci. 1952, 19, 848–849. [Google Scholar] [CrossRef]
- Miles, J. On virtual mass and transient motion in subsonic compressible flow. Q. J. Mech. Appl. Math. 1951, 4, 388–400. [Google Scholar] [CrossRef]
- Vepa, R. Finite State Modeling of Aeroelastic Systems; Technical Report; NASA Contractor Report 2779; NASA: Washington, DC, USA, 1977.
- Fonte, F.; Ricci, S.; Mantegazza, P. Gust load alleviation for a regional aircraft through a static output feedback. J. Aircr. 2015, 52, 1559–1574. [Google Scholar] [CrossRef]
- Eversman, W.; Tewari, A. Modified exponential series approximation for the Theodorsen function. J. Aircr. 1991, 28, 553–557. [Google Scholar] [CrossRef]
- Quero, D. An Aeroelastic Reduced Order Model for Dynamic Response Prediction to Gust Encounters. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Kaiser, C.; Freidewald, D.; Quero, D.; Nitzsche, J. Aeroelastic Gust Load Prediction based on Time-Linearized RANS Solutions. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Braunschweig, Germany, 13–15 September 2016. [Google Scholar]
- Poussot-Vassal, C.; Quero, D.; Vuillemin, P. Data-driven approximation of a high fidelity gust-oriented flexible aircraft dynamical model. In Proceedings of the 9th International Conference on Mathematical Modelling, Vienna, Austria, 21–23 February 2018. [Google Scholar] [CrossRef]
- Blair, M. A Compilation of the Mathematics Leading to the Doublet Lattice Method; Technical Report; Air Force Wright Laboratory: Dayton, OH, USA, 1992. [Google Scholar]
- Rodden, W.; Farkas, W.; Heathera, M.; Kliszewski, A. Aerodynamic Influence Coefficients From Piston Theory: Analytical Development and Computational Procedure; TDR-169-(3230-11)-TN-2; Aerospace Corp.: El Segundo, CA, USA, 1962. [Google Scholar]
- Sears, W. A Systematic Presentation of the Theory of Thin Airfoils in Non-Uniform Motion. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1938. [Google Scholar]
- Friedewald, D.; Thormann, R.; Kaiser, C.; Nitzsche, J. Quasi-steady doublet-lattice correction for aerodynamic gust response prediction in attached and separated transonic flow. CEAS Aeronaut. J. 2018, 9, 53–66. [Google Scholar] [CrossRef]
- Smith, T.A.; Hakanson, J.; Nair, S.; Yurkovich, R. State-space model generation for flexible aircraft. J. Aircr. 2004, 41, 1473–1481. [Google Scholar] [CrossRef]
- Beckert, A.; Wendland, H. Multivariate interpolation for fluid-structure-interaction problems using radial basis functions. Aerosp. Sci. Technol. 2001, 5, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Reschke, C. Integrated Flight Loads Modelling and Analysis for Flexible Transport Aircraft. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2006. [Google Scholar]
- Klimmek, T. Parametric set-up of a structural model for FERMAT configuration aeroelastic and loads analysis. J. Aeroelasticity Struct. Dyn. 2014, 3. [Google Scholar] [CrossRef]
- MSC Software Corporation (Ed.) Aeroelastic Analysis User’s Guide, version 68; MSC Software Corporation: Santa Ana, CA, USA, 2004. [Google Scholar]

















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quero, D.; Vuillemin, P.; Poussot-Vassal, C. A Generalized State-Space Aeroservoelastic Model Based on Tangential Interpolation. Aerospace 2019, 6, 9. https://doi.org/10.3390/aerospace6010009
Quero D, Vuillemin P, Poussot-Vassal C. A Generalized State-Space Aeroservoelastic Model Based on Tangential Interpolation. Aerospace. 2019; 6(1):9. https://doi.org/10.3390/aerospace6010009
Chicago/Turabian StyleQuero, David, Pierre Vuillemin, and Charles Poussot-Vassal. 2019. "A Generalized State-Space Aeroservoelastic Model Based on Tangential Interpolation" Aerospace 6, no. 1: 9. https://doi.org/10.3390/aerospace6010009