3.1. Wearable Antenna Optimization
The wearable antenna was optimized with Pareto–Estra algorithm that was tuned basing on the dipole benchmark problem. For this purpose, we set parameters values to
p = 0.25 and
q = 0.7 because this specific combination allowed to obtain very good impedance matching and antenna gain for a small number of objective function calls, which was equal to 34 (according to line 19 in
Table 3).
We started our numerical experiment with optimization of the antenna that has one circle only; this is the classical design of UWB circular monopole antenna. There were 3 design parameters: a, b and r1. The ground rectangle can be integrated with a printed circuit board that contains electronic circuits. The dimensions of the ground plane (a, b parameters) were limited to 5 cm because we wanted to keep the antenna as small as possible, which is crucial for a wearable application. The maximum radius of the circle allowed in optimization procedure was equal to 25 mm.
The initial set of design parameter values was selected by trial and error. This provided the starting point for antenna optimization using the P-EStra algorithm. The initial values of design parameters were the following:
r1start = 0.0228,
astart = 0.033,
bstart = 0.033. For this starting point the
VSWR component of the objective function was
VSWRstart = 3.64 and the Gain component was G
start = 0.28 dBi. The constraints in the optimization process were geometry oriented, allowing only for sets of design variable values that preserved the assumed geometry of the antenna without self-intersections or overlapping sections. The optimization process required 56 iterations to satisfy the automatic stopping condition. The condition relies on the ratios of the standard deviation within the current iteration
to the initial standard deviation iteration
d0k for each
k-th optimization variable. The deviation is normalized across all the variables. The process stops when
. where s << 1 is a prescribed search tolerance. This corresponds to the situation when the current search region is sufficiently small for all variables. In this study, basing on experience gathered on optimization of benchmark problem, we assumed
. Final set of parameters was identified with 56 iterations
r1stop = 0.02366.
astop = 0.02241.
bstop = 0.04619 and the final objective function components were the following:
Gstop = 2.08.
VSWRstop = 2.36. The final geometry of antenna and its radiation pattern is presented in
Figure 10.
Table 4 presents the parameters of optimized antenna:
VSWR, gain G and realized gain (RG) for all 4 bands.
The optimization of single circle antenna improved it performance, but its impedance matching is still insufficient. To find the geometry that would have better performance we optimized antenna that consisted of 2 circles. Initial values of design parameters r1start. astart and bstart were the same as final parameter*rs of single circle antenna. The set of initial parameters had the following values: r1start = 0.02366. r2start = 0.02. x2start = 0.025 y2start = 0. astart = 0.02241. bstart = 0.04619 For this starting point the VSWR component of the objective function was VSWRstart = 2.26 and the Gain component was Gstart = 1.33 dBi.
The final set of parameters of two circle antenna was identified with 54 iterations. The final values of design parameters are the following:
r1stop = 0.0209.
r2stop = 0.016.
x2stop = 0.0216.
y2stop = 0.0225.
astop = 0.02388.
bstop = 0.02217. The final values of objective function components were and
Gstop = 1.98.
VSWRstop = 2.26. The final geometry of antenna and its radiation pattern is presented in
Figure 11.
Table 5 presents the parameters of optimized antenna:
VSWR. gain G and realized gain (RG) for all 4 bands.
The double circle antenna exhibits a performance slightly better than the one of the single circle antennae. In this case, VSWR was reduced from 2.36 to 2.26. The gain was similar in both cases: 2.08 dBi for single circle and 1.98 dBi for two circles and is comparable to half-wave dipole antenna.
Since we design wearable antenna, we wanted to obtain better impedance matching because the presence of clothes can detune the antenna. Having better impedance matching, there would be some tolerance to this effect even for antenna covered with other materials. For this reason, we have investigated a more complex antenna geometry, that consists of 3 circles. Adding another circle brings 3 more design variables, which in turn increases the number of iterations and overall computational cost of optimization procedure. In our opinion, 3 circle antennae that are controlled by 9 design variables implies a feasible number of parameters to handle by P-EStra algorithm. Initial values of design parameters were inspired by the geometry of optimized two circle antenna and had following values: r1start = 0.0209, r2start = 0.016, x2start = 0.0216, y2start = 0.0225, r3start = 0.00279, x3start = 0.02793, y3start = −0.01242, astart = 0.02388, bstart = 0.02217. For this starting point, the VSWR component of the objective function was VSWRstart = 2.21 and the Gain component was Gstart = 2.0 dBi.
The history of the optimization process from the initial point in the objective function space is shown in
Figure 12. The final set of parameters of two circle antenna was identified after 87 iterations. The final values of design parameters are the following:
r1stop = 0.02195,
r2stop = 0.01852,
x2stop = 0.02552,
y2stop = 0.01648,
r3stop = 0.00266,
x3stop = 0.02725,
y3stop = −0.02574,
astop = 0.02384,
bstop = 0.0226. The final values of objective function components were
Gstop = 2.08,
VSWRstop = 1.76. The final geometry of the antenna and its radiation pattern is shown in
Figure 13.
Table 6 presents the parameters of optimized antenna:
VSWR, gain G and realized gain (RG) for all four bands.
The antenna with 3 circles has the best impedance matching compared to single circle antenna and two circle antennae. The maximum value of
VSWR is 1.76. At the same time the minimum value of Gain is 2.08. The smallest value of realized gain was for 1.8 GHz and was equal to 2.05 dBi. Current distribution for antenna with 3 circles is presented in
Table 7 for all 4 considered frequencies.
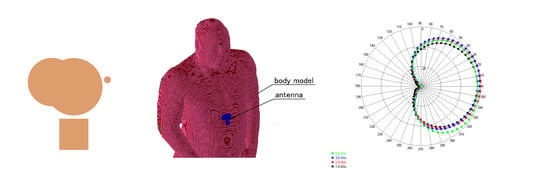
Wearable antenna was optimized with simplified model of human body that represents only its part with cylindrical structure. To verify the radiation pattern of three circle antenna in more realistic scenario, we have used heterogenous model of entire body that is available in Remcom Xfdtd program. It has 3mm voxel size and models not only the shape of human body, but also the inner tissues. We assumed that the antenna is located in the front of the torso, at the distance of 10 mm from the surface of the model.
Figure 14 presents the position of antenna on heterogenous model and obtained radiation pattern in horizontal plane. The results are very similar to those obtained with simplified model. The maximum gain varies in this case form 2.5 dBi for 1.8 GHz to 4.5 dBi for 2.5 GHz.
In
Figure 15 the impedance matching of three optimized antennas is presented for on-body position. It is evident that optimized 3 circle antennae have the best impedance matching for all considered bands from 1.8 GHz to 5.8 GHz.
Wearable antenna is the source of electromagnetic wave that is partially absorbed by the human body. This effect can be illustrated with Specific Absorption Rate (SAR) parameter that presents the amount of energy dissipated by the mass of human tissues. For the optimized antenna with three circular elements, we have simulated the SAR parameter using heterogenous model of human body that is available in Remcom Xfdtd software. The possible application of this antenna could be the portable, battery operated device with limited power resources. Thus, for SAR simulations we have assumed that the power of transmitter connected to the antenna is 200 mW, which corresponds to the power class 2 of LTE and 5 G portable terminals. The distribution of the SAR parameter on the cross-section of the body is presented in
Figure 16. It shows that the body region that is close to the antenna absorbs the most of energy. The maximum values of SAR (SAR
max) and average values for the whole body (SAR
AVG) averaged for 10 g of tissue are presented in
Table 8 for all considered bands. The SAR values are below the limits for mobile phones that for Europe are 2 W/kg.
3.2. Assessment of Antenna Prototype
The impedance matching of the optimized antenna was experimentally assessed using a prototype. We used DuPont Pyralux
® material that is a polymer foil with one side of coper metallization. The thickness of the base material is only 25 μm and the thickness of metallization is 35 μm. This makes the antenna flexible and lightweight what is beneficial in wearable applications. The dielectric constant of base material given by the manufacturer is ε
r = 3.4 and the dielectric loss tg(δ) = 0.005; however, in our previous research we have found that its effective value that can be used for numerical simulation with voxels that are thicker than the substrate (0.1 mm in our case) is ε
r = 1.7 and the dielectric loss tg(δ) = 0.001 [
20] Due to the small thickness of substrate and its flexibility we used laser printer to put the mask on the substrate. To make it solid, we printed 4 layers of mask and then etched the metallization. The prototype is presented in
Figure 17. The impedance matching of the prototype antenna located on human subject was measured using a Rohde & Schwarz ZVB 14 vector network analyzer. To avoid reflections that may influence the results of measurements they were conducted in anechoic chamber. The antenna was attached to the torso of human subject. To control the distance between antenna and human body we have used the Styrofoam spacer that is presented in
Figure 18. The prototype antenna was fed by a coaxial probe and the calibration plane was moved to the end of the coaxial cable.
The impedance matching of the prototype for antenna located 10 mm, 20 mm and 30 mm from body are presented in
Figure 19,
Figure 20,
Figure 21. The results of measurements are compared with results of simulations obtained with NMR human body model. The results of measurements are similar to the results of simulations. The impedance matching of the prototype antenna is satisfactory in all assumed bands, with
VSWR < 2.2. For the antenna located 10 mm from body, the
VSWR value for 5.8 GHz is 2.2, which may result from a difference between a numerical model of the body and a human subject.
The radiation pattern of the prototype antenna was measured in anechoic setup presented in
Figure 22. The measurement antenna was a Rohde & Schwarz HF 907. It was connected to a Rohde & Schwarz SMB 100A signal generator. The prototype antenna was attached to human subject that was standing on the turntable. For each angle of rotation (with 5 degrees step), the power of signal was measured with Rohde & Schwarz FSC 6 spectrum analyzer. The antenna gain was measured using gain comparison method [
21]. After the experiment, the human subject and prototype antenna were replaced with second Rohde & Schwarz HF 907 that we used as standard gain antenna, for which the received power was measured. Knowing the gain of HF 907 antenna, we then recalculated received power level into antenna gain. The results of radiation pattern and antenna gain measurements are presented in
Table 9.
Results of radiation pattern measurements correspond with results of simulations. Some difference may result with antenna placement on the body that could be slightly different in the case of simulations and measurements. The antenna gain obtained from measurements was slightly lower than obtained from simulations. This could be caused by losses introduced by feeding cable.