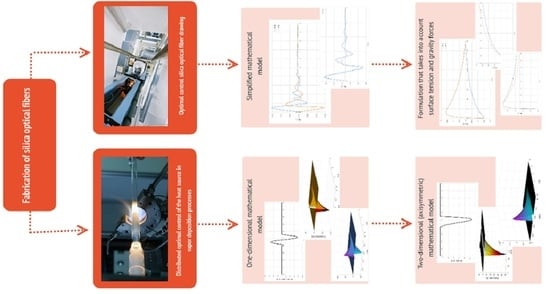
Fabrication of Silica Optical Fibers: Optimal Control Problem Solution
Abstract
:1. Introduction
- MCVD is the modified chemical vapor deposition;
- OVD is the outside vapor deposition;
- VAD is the vapor axial deposition;
- plasma-chemical methods (PMCVD, PCVD, etc.).
Motivation
- (a)
- To control and manage the allowing processes by the MCVD method and the drawing of optical fibers not by measuring the temperature and fiber diameter at only one point, as it is done now, but by measuring these parameters over extended sections (by length). In other words, to conduct a distributed observation;
- (b)
- To control the process not with the help of PID controllers, as it is done now, but based on the theory of the optimal control of distributed systems.
2. Distributed Optimal Control of the Heat Source in Vapor Deposition Processes
2.1. One-Dimensional Mathematical Model of MCVD Process
2.2. Solution of the Distributed Optimal Control Problem
2.3. General Results
3. Boundary Optimal Control of the Heat Source in Vapor Deposition Processes
3.1. Two-Dimensional (Axisymmetric) Mathematical Model of MCVD Process
3.2. Solution of the Boundary Optimal Control Problem
3.3. Adjustment and Experimental Determination of the Parameters of a Moving Exposure Source
4. Optimal Control of Silica Optical Fiber Drawing
4.1. Optimal Control Problem: A Simplified Mathematical Model of Fiber Drawing
- Searching for a stationary solution of the system (34) (i.e., definition of functions and );
- Determination of a function depending on stationary states;
- Searching for a solution of the optimality system (47) and finding the optimal control function (the numerical solution of the optimality system (47) was implemented using the Comsol Multiphysics modeling package);
- Result analysis.
4.2. Optimal Control Problem for the Optical Fiber Drawing in a Formulation That Takes into Account Surface Tension and Gravity Forces
- Searching for a stationary solution. These functions were found using the solution of system, which describes the stationary state of drawing process [23];
- Finding the functions , , , and , depending on stationary states;
- Solving of the optimality system (52) and finding the optimal control function ;
- Result analysis.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J.; et al. Roadmap of optical communications. J. Opt. 2016, 18, 063002. [Google Scholar] [CrossRef]
- Ferreira, M.F.S. Optical Fibers: Technology, Communications and Recent Advances; Nova Science Publishers: New York, NY, USA, 2017; ISBN 9781536109917. [Google Scholar]
- Cordeiro, C.M.B.; Ng, A.K.L.; Ebendorff-Heidepriem, H. Ultra-simplified Single-Step Fabrication of Microstructured Optical Fiber. Sci. Rep. 2020, 10, 9678. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Guo, H. A review of SLMed magnesium alloys: Processing, properties, alloying elements and postprocessing. Metals 2020, 10, 1073. [Google Scholar] [CrossRef]
- Anuszkiewicz, A.; Kasztelanic, R.; Filipkowski, A.; Stepniewski, G.; Stefaniuk, T.; Siwicki, B.; Pysz, D.; Klimczak, M.; Buczynski, R. Fused silica optical fibers with graded index nanostructured core. Sci. Rep. 2018, 8, 12329. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; An, L. Abnormal behavior of silica doped with small amounts of aluminum. Sci. Rep. 2016, 6, 6–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hehlen, M.; Epstein, R.; Patterson, W.; Sheik-Bahae, M.; Seletskiy, D. Measurement of solid-state optical refrigeration by two-band differential luminescence thermometry. J. Opt. Soc. Am. B 2009, 27, 611–618. [Google Scholar]
- Orlov, L.K.; Vdovin, V.I.; Drozdov, Y.N.; Orlov, M.L.; Ivina, N.L.; Steinman, E.A. Characterization of Interface Layers of a Solid Solution Formed During the Growth of a Carbide Layer on Silicon from Hydrogen Containing Compounds. J. Struct. Chem. 2021, 62, 630–640. [Google Scholar] [CrossRef]
- Saadi, N.S.; Hassan, L.B.; Karabacak, T. Metal oxide nanostructures by a simple hot water treatment. Sci. Rep. 2017, 7, 7158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P. Modeling the fabrication of hollow fibers: Capillary drawing. J. Light. Technol. 2001, 19, 1924–1931. [Google Scholar] [CrossRef]
- Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P.; Richardson, D.J. The mathematical modelling of capillary drawing for holey fibre manufacture. J. Eng. Math. 2002, 43, 201–227. [Google Scholar] [CrossRef]
- Kostecki, R.; Ebendorff-Heidepriem, H.; Warren-Smith, S.C.; Monro, T.M. Predicting the drawing conditions for Microstructured Optical Fiber fabrication. Opt. Mater. Express 2014, 4, 29. [Google Scholar] [CrossRef] [Green Version]
- Kostecki, R.; Ebendorff-heidepriem, H.; Davis, C.; Mcadam, G.; Warren-smith, S.C.; Monro, T.M. Silica exposed-core microstructured optical fibers. Opt. Mater. Express 2012, 2, 5082–5087. [Google Scholar] [CrossRef]
- Monro, T.M.; Richardson, D.J. Holey optical fibres: Fundamental properties and device applications. Comptes Rendus Phys. 2003, 4, 175–186. [Google Scholar] [CrossRef]
- Badii, M. Periodic solutions for a class of degenerate evolution problems. Nonlinear Anal. Theory Methods Appl. 2001, 44, 499–508. [Google Scholar] [CrossRef]
- Kubyshkin, V.A.; Finyagina, V.I. Podvizhnoe Upravlenie v Sistemah s Raspredelennymi Parametrami; SINTEG: Moscow, Russia, 2005. [Google Scholar]
- Lienard, I.V.; John, H. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Rappoport, E.Y. Analiz i Sintez Sistem Avtomaticheskogo Upravleniya s Raspredelennymi Parametrami; Vysshaya Shkola: Moscow, Russia, 2005. [Google Scholar]
- Fursikov, A.V. Optimalnoe Upravlenie Raspredelennymi Sistemami. Teoriya i Prilozheniya; Nauchnaya Kniga: Moscow, Russia, 1999. [Google Scholar]
- Morgan, R. Linearization and Stability Analysis of Nonlinear Problems. Rose-Hulman Undergrad. Math. J. 2015, 16, 67–91. [Google Scholar]
- Rodríguez, R.S.; Avalos, G.G.; Gallegos, N.B.; Ayala-jaimes, G.; Garcia, A.P. SS symmetry Approximation of Linearized Systems to a Class of Nonlinear Systems Based on Dynamic Linearization. Symmetry 2021, 13, 854. [Google Scholar] [CrossRef]
- Pervadchuk, V.; Vladimirova, D.; Gordeeva, I. Optimal control of distributed systems in problems of quartz optical fiber production. In AIP Conference Proceedings; AIP Publishing LLC.: Huntington, NY, USA, 2018; p. 020036. [Google Scholar]
- Hallen, M.; Li, B.; Tanouchi, Y.; Tan, C.; West, M.; You, L. Computation of steady-state probability distributions in stochastic models of cellular networks. PLoS Comput. Biol. 2011, 7, e1002209. [Google Scholar] [CrossRef] [PubMed]
























Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pervadchuk, V.; Vladimirova, D.; Gordeeva, I.; Kuchumov, A.G.; Dektyarev, D. Fabrication of Silica Optical Fibers: Optimal Control Problem Solution. Fibers 2021, 9, 77. https://doi.org/10.3390/fib9120077
Pervadchuk V, Vladimirova D, Gordeeva I, Kuchumov AG, Dektyarev D. Fabrication of Silica Optical Fibers: Optimal Control Problem Solution. Fibers. 2021; 9(12):77. https://doi.org/10.3390/fib9120077
Chicago/Turabian StylePervadchuk, Vladimir, Daria Vladimirova, Irina Gordeeva, Alex G. Kuchumov, and Dmitrij Dektyarev. 2021. "Fabrication of Silica Optical Fibers: Optimal Control Problem Solution" Fibers 9, no. 12: 77. https://doi.org/10.3390/fib9120077