Bonding Strength Effects in Hydro-Mechanical Coupling Transport in Granular Porous Media by Pore-Scale Modeling
Abstract
:1. Introduction
2. Numerical Methods
2.1. Lattice Boltzmann Method (LBM)
2.2. Discrete Element Method (DEM)
2.3. Fluid and Solid Interaction
3. Benchmarks
3.1. Single Particle Sedimentation
3.2. Two-Particle Sedimentation
4. Numerical Results and Discussion
4.1. Biaxial Compression Simulation
4.2. Sand Production Simulation
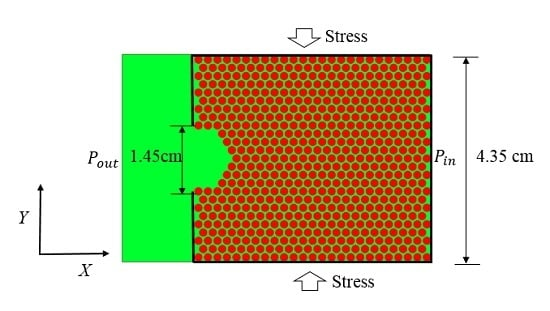
4.2.1. Physical Model
4.2.2. Damage Evolution
4.2.3. Effect of Bonding Strength
4.2.4. The Effect of Flow Rate
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ranjith, P.G.; Perera, M.S.A.; Perera, W.K.G.; Wu, B.; Choi, K.S. Effective parameters for sand production in unconsolidated formations: An experimentl study. J. Petrol. Sci. Eng. 2013, 105, 34–42. [Google Scholar] [CrossRef]
- Papamichos, E. Erosion and multiphase flow in porous media: Application to sand production. Eur. J. Environ. Civ. Eng. 2010, 14, 1129–1154. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Pereraa, M.S.A.; Pereraa, W.K.G.; Choib, S.K.; Yasarc, E. Sand production during the extrusion of hydrocarbons from geological formations: A review. J. Petrol. Sci. Eng. 2014, 124, 72–82. [Google Scholar] [CrossRef]
- Van den Hoek, P.; Hertogh, G.M.M.; Kooijman, A.P.; de Bree, P.; Kenter, C.J.; Papamichos, E. A new concept of sand production prediction: Theory and laboratory experiments. SPE Drill. Complet. 2000, 15, 261–273. [Google Scholar] [CrossRef]
- Tronvoll, J.; Skj, A.; Papamichos, E. Sand production: Mechanical failure or hydrodynamic erosion? Int. J. Rock Mech. Min. Sci. 1997, 34, 291. [Google Scholar] [CrossRef]
- Vardoulakis, I.; Stavropoulou, M.; Papanastasiou, P. Hydro-mechanical aspects of the sand production problem. Transp. Porous Med. 1996, 22, 225–244. [Google Scholar] [CrossRef]
- Boutt, D.F.; Cook, B.K.; Williams, J.R. A coupled fluid-solid model for problems in geomechanics: Application to sand production. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 997–1018. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- O’Connor, R.M.; Torczynski, J.R.; Preece, D.S.; Klosek, J.T.; Williams, J.R. Discrete element modeling of sand production. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1997, 34, 231. [Google Scholar] [CrossRef]
- Jensen, R.P.; Preece, D.S. Modeling Sand Production with Darcy-Flow Coupled with Discrete Elements; Sandia National Labs: Albuquerque, NM, USA; Livermore, CA, USA, 2000.
- Zhou, Z.Y.; Yu, A.B.; Choi, S.K. Numerical simulation of the liquid-induced erosion in a weakly bonded sand assembly. Powder Technol. 2011, 211, 237–249. [Google Scholar] [CrossRef]
- Climent, N.; Arroyoa, M.; O’Sullivanb, C.; Gensa, A. Sand production simulation coupling DEM with CFD. Eur. J. Environ. Civ. Eng. 2014, 18, 983–1008. [Google Scholar] [CrossRef]
- Li, L.; Papamichos, E.; Cerasi, P. Investigation of sand production mechanisms using DEM with fluid flow. In Proceedings of the International Symposium of the International Society for Rock Mechanics (Eurock’06), Liege, Belgium, 13–15 August 2014.
- Han, Y.; Cundall, P.A. LBM-DEM modeling of fluid-solid interaction in porous media. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1391–1407. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wang, M.; Chen, S. Electroosmosis in homogeneously charged micro- and nanoscale random porous media. J. Coll. Interface Sci. 2007, 314, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Rep. 2008, 63, 1–30. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Aidun, C.K.; Lu, Y.; Ding, E.J. Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 1998, 373, 287–311. [Google Scholar] [CrossRef]
- Chen, Y.; Kanga, Q.; Caia, Q.; Wanga, M.; Zhang, D. Lattice Boltzmann Simulation of Particle Motion in Binary Immiscible Fluids. Commun. Comput. Phys. 2015, 18, 757–786. [Google Scholar] [CrossRef]
- Ghassemi, A.; Pak, A. Numerical simulation of sand production experiment using a coupled Lattice Boltzmann-Discrete Element Method. J. Petrol. Sci. Eng. 2015, 135, 218–231. [Google Scholar] [CrossRef]
- Velloso, R.Q.; Vargas, E.A.; Goncalves, C.J.; Prestes, A. Analysis of sand production processes at the pore scale using the discrete element method and lattice Boltzman procedures. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010.
- Tronvoll, J.; Papamichos, E.; Skjaerstein, A.; Sanfilippo, F. Sand production in ultra-weak sandstones: Is sand control absolutely necessary? In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 30 August–3 September 1997.
- Jiang, M.; Yu, H.S.; Leroueil, S. A simple and efficient approach to capturing bonding effect in naturally microstructured sands by discrete element method. Int. J. Numer. Methods Eng. 2007, 69, 1158–1193. [Google Scholar] [CrossRef]
- Servant, G.; Marchina, P.; Nauroy, J.F. Near Wellbore Modeling: Sand Production Issues. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007.
- Wang, M.; Kang, Q.J.; Pan, N. Thermal conductivity enhancement of carbon fiber composites. Appl. Ther. Eng. 2009, 29, 418–421. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N.; Wang, J.; Chen, S. Lattice Poisson-Boltzmann simulations of electroosmotic flows in charged anisotropic porous media. Commun. Comput. Phys. 2007, 2, 1055–1070. [Google Scholar]
- Wang, M.; Kang, Q.; Viswanathan, H.; Robinson, B. Modeling of electro-osmosis of dilute electrolyte solutions in silica microporous media. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Wang, M.R.; Kang, Q.J. Electrokinetic Transport in Microchannels with Random Roughness. Anal. Chem. 2009, 81, 2953–2961. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, M.R. Modeling of electrokinetic reactive transport in micropore using a coupled lattice Boltzmann method. J. Geophys. Res. Solid Earth 2015, 120, 2877–2890. [Google Scholar] [CrossRef]
- Yang, X.; Mehmanib, Y.; Perkinsa, W.A.; Pasqualic, A.; Schönherrc, M.; Kimd, K.; Peregod, M.; Parksd, M.L.; Traske, N.; Balhoff, M.T. Intercomparison of 3D pore-scale flow and solute transport simulation methods. Adv. Water Resour. 2015. [Google Scholar] [CrossRef]
- Kang, Q.J.; Zhang, D.X.; Chen, S.Y. Displacement of a two-dimensional immiscible droplet in a channel. Phys. Fluids 2002, 14, 3203–3214. [Google Scholar] [CrossRef]
- Huang, H.B.; Lu, X.Y. Relative permeabilities and coupling effects in steady-state gas-liquid flow in porous media: A lattice Boltzmann study. Phys. Fluids 2009, 21, 092104. [Google Scholar] [CrossRef]
- Huang, H.B.; Wang, L.; Lu, X.Y. Evaluation of three lattice Boltzmann models for multiphase flows in porous media. Comput. Math. Appl. 2010, 61, 3606–3617. [Google Scholar] [CrossRef]
- Huang, H.B.; Huang, J.J.; Lu, X.Y. Study of immiscible displacements in porous media using a color-gradient-based multiphase lattice Boltzmann method. Comput. Fluids 2014, 93, 164–172. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.; Tao, W. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, Q.; Xia, Z.; Wang, M.; Chen, S. Momentum-exchange method in lattice Boltzmann simulations of particle-fluid interactions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 88, 013303. [Google Scholar] [CrossRef] [PubMed]
- De Rosis, A. On the dynamics of a tandem of asynchronous flapping wings: Lattice Boltzmann-immersed boundary simulations. Phys. A Stat. Mech. Appl. 2014, 410, 276–286. [Google Scholar] [CrossRef]
- Cao, C.; Chen, S.; Li, J.; Liu, Z.; Zha, L.; Bao, S.; Zheng, C. Simulating the interactions of two freely settling spherical particles in Newtonian fluid using lattice-Boltzmann method. Appl. Math. Comput. 2015, 250, 533–551. [Google Scholar] [CrossRef]
- Galindo-Torres, S. A coupled Discrete Element Lattice Boltzmann Method for the simulation of fluid-solid interaction with particles of general shapes. Comput. Methods Appl. Mech. Eng. 2013, 265, 107–119. [Google Scholar] [CrossRef]
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98. [Google Scholar] [CrossRef]
- Jiang, M.; Yan, H.B.; Zhu, H.H.; Utili, S. Modeling shear behavior and strain localization in cemented sands by two-dimensional distinct element method analyses. Comput. Geotech. 2011, 38, 14–29. [Google Scholar] [CrossRef]
- Wen, B.; Li, H.; Zhang, C.; Fang, H. Lattice-type-dependent momentum-exchange method for moving boundaries. Phys. Rev. E 2012, 85, 016704. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Hu, H.H.; Joseph, D.D. Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid Part 1. Sedimentation. J. Fluid Mech. 1994, 261, 95–134. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T.; Peng, Y. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows. Phys. Lett. Sect. A Gen. Atom. Solid State Phys. 2006, 354, 173–182. [Google Scholar] [CrossRef]
- Fortes, A.F.; Joseph, D.D.; Lundgren, T.S. Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 1987, 177, 467–483. [Google Scholar] [CrossRef]
- Galindo-Torres, S.; Pedroso, D.M.; Williams, D.J.; Mühlhaus, H.B. Strength of non-spherical particles with anisotropic geometries under triaxial and shearing loading configurations. Granul. Matter 2013, 15, 531–542. [Google Scholar] [CrossRef]
- Wang, Y.H.; Leung, S.C. A particulate-scale investigation of cemented sand behavior. Can. Geotech. J. 2008, 45, 29–44. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P.; Maxwell, S. Micromechanical modeling of cracking and failure in brittle rocks. J. Geophys. Res. Solid Earth 2000, 105, 16683–16697. [Google Scholar] [CrossRef]













| Parameter | Value |
|---|---|
| Number of particle | 600 |
| Diameter of particle | 2 mm |
| 2.5 × 104 N/m | |
| 1.0 × 104 N/m | |
| μ | 0.2 |
| Low bonding strength | 0.0078 N |
| Middle bonding strength | 0.039 N |
| High bonding strength | 0.078 N |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xie, C.; Chen, Y.; Wang, M. Bonding Strength Effects in Hydro-Mechanical Coupling Transport in Granular Porous Media by Pore-Scale Modeling. Computation 2016, 4, 15. https://doi.org/10.3390/computation4010015
Chen Z, Xie C, Chen Y, Wang M. Bonding Strength Effects in Hydro-Mechanical Coupling Transport in Granular Porous Media by Pore-Scale Modeling. Computation. 2016; 4(1):15. https://doi.org/10.3390/computation4010015
Chicago/Turabian StyleChen, Zhiqiang, Chiyu Xie, Yu Chen, and Moran Wang. 2016. "Bonding Strength Effects in Hydro-Mechanical Coupling Transport in Granular Porous Media by Pore-Scale Modeling" Computation 4, no. 1: 15. https://doi.org/10.3390/computation4010015