Debye-Hückel Free Energy of an Electric Double Layer with Discrete Charges Located at a Dielectric Interface
Abstract
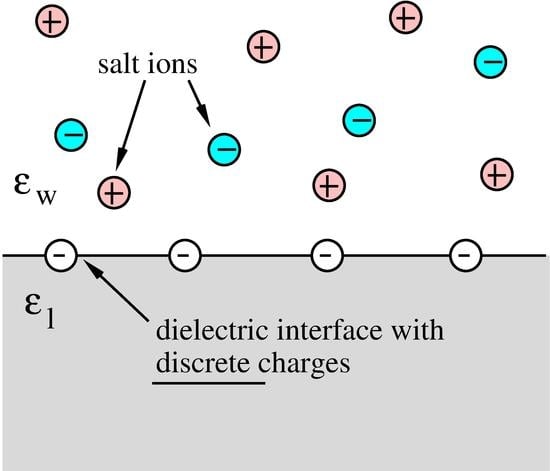
:1. Introduction
2. Theory and Discussion
2.1. Ensemble of Charged Disks
2.2. Single Isolated Charged Disk
2.3. Debye-Hückel Free Energy
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Attard, P. Electrolytes and the electric double layer. Adv. Chem. Phys. 1996, 92, 1–160. [Google Scholar]
- Andelman, D. Introduction to electrostatics in soft and biological matter. In Soft Condensed Matter Physics in Molecular and Cell Biology; Poon, W.C.K., Andelman, D., Eds.; Taylor & Francis: New York, NY, USA, 2006; Chapter 6. [Google Scholar]
- Langner, M.; Kubica, K. The electrostatics of lipid surfaces. Chem. Phys. Lipids 1999, 101, 3–35. [Google Scholar] [CrossRef]
- Marrink, S.J.; Corradi, V.; Souza, P.C.; Ingolfsson, H.I.; Tieleman, D.P.; Sansom, M.S. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, S. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 113–136. [Google Scholar] [CrossRef] [PubMed]
- Andelman, D. Electrostatic properties of membranes: The Poisson–Boltzmann theory. In Handbook of Biological Physics; Elsevier: Amsterdam, The Netherlands, 1995; Volume 1, pp. 603–642. [Google Scholar]
- Ben-Yaakov, D.; Andelman, D.; Harries, D.; Podgornik, R. Beyond standard Poisson–Boltzmann theory: Ion-specific interactions in aqueous solutions. J. Phys. Condens. Matter 2009, 21, 424106. [Google Scholar] [CrossRef] [PubMed]
- Bohinc, K.; Bossa, G.V.; May, S. Incorporation of ion and solvent structure into mean-field modeling of the electric double layer. Adv. Colloid Interface Sci. 2017, 249, 220–233. [Google Scholar] [CrossRef]
- Lukatsky, D.; Safran, S. Universal reduction of pressure between charged surfaces by long-wavelength surface charge modulation. EPL 2002, 60, 629. [Google Scholar] [CrossRef] [Green Version]
- Adar, R.M.; Andelman, D.; Diamant, H. Electrostatics of patchy surfaces. Adv. Colloid Interface Sci. 2017, 247, 198–207. [Google Scholar] [CrossRef] [Green Version]
- Ghosal, S.; Sherwood, J.D. Screened Coulomb interactions with non-uniform surface charge. Proc. R. Soc. A 2017, 473, 20160906. [Google Scholar] [CrossRef] [Green Version]
- Frydel, D. General theory of charge regulation within the Poisson–Boltzmann framework: Study of a sticky-charged wall model. J. Chem. Phys. 2019, 150, 194901. [Google Scholar] [CrossRef] [PubMed]
- Mbamala, E.C.; Ben-Shaul, A.; May, S. Domain formation induced by the adsorption of charged proteins on mixed lipid membranes. Biophys. J. 2005, 88, 1702–1714. [Google Scholar] [CrossRef] [Green Version]
- Himeno, H.; Shimokawa, N.; Komura, S.; Andelman, D.; Hamada, T.; Takagi, M. Charge-induced phase separation in lipid membranes. Soft Matter 2014, 10, 7959–7967. [Google Scholar] [CrossRef] [Green Version]
- Betterton, M.; Brenner, M.P. Electrostatic edge instability of lipid membranes. Phys. Rev. Lett. 1999, 82, 1598. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.H.; Kang, I.S.; Lee, C.M. Electrostatic contribution to line tension in a wedge-shaped contact region. Langmuir 2003, 19, 9334–9342. [Google Scholar] [CrossRef]
- Bossa, G.V.; Brown, M.A.; Bohinc, K.; May, S. Modeling the electrostatic contribution to the line tension between lipid membrane domains using Poisson–Boltzmann theory. Int. J. Adv. Eng. Sci. Appl. Math. 2016, 8, 101–110. [Google Scholar] [CrossRef]
- Bell, G.; Mingins, J.; Levine, S. Cell and hexagonal lattice models for adsorbed ions in electrical double layer theory. Trans. Faraday Soc. 1966, 62, 949–959. [Google Scholar] [CrossRef]
- Cole, K. Zeta potential and discrete vs. uniform surface charges. Biophys. J. 1969, 9, 465. [Google Scholar] [CrossRef] [Green Version]
- Nelson, A.P.; McQuarrie, D. The effect of discrete charges on the electrical properties of a membrane. I. J. Theor. Biol. 1975, 55, 13–27. [Google Scholar] [CrossRef]
- Stillinger Jr, F.H. Interfacial Solutions of the Poisson–Boltzmann Equation. J. Chem. Phys. 1961, 35, 1584–1589. [Google Scholar] [CrossRef] [Green Version]
- Mathias, R.T.; Baldo, G.J.; Manivannan, K.; Mclaughlin, S. Discrete charges on biological membranes. In Electrified Interfaces in Physics, Chemistry and Biology; Springer: Berlin/Heidelberg, Germany, 1992; pp. 473–490. [Google Scholar]
- Arakelian, V.; Walther, D.; Donath, E. Electric potential distributions around discrete charges in a dielectric membrane—Electrolyte solution system. Colloid Polym. Sci. 1993, 271, 268–276. [Google Scholar] [CrossRef]
- Messina, R. Effect of image forces on polyelectrolyte adsorption at a charged surface. Phys. Rev. E 2004, 70, 051802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enos, B.E.; McQuarrie, D.A. The effect of discrete charges on the electrical properties of membranes. II. J. Theor. Biol. 1981, 93, 499–522. [Google Scholar] [CrossRef]
- Stigter, D.; Dill, K.A. Interactions in dilute monolayers of long-chain ions at the interface between n-heptane and aqueous salt solutions. Langmuir 1986, 2, 791–796. [Google Scholar] [CrossRef]
- Khan, M.O.; Petris, S.; Chan, D.Y. The influence of discrete surface charges on the force between charged surfaces. J. Chem. Phys. 2005, 122, 104705. [Google Scholar] [CrossRef] [PubMed]
- Madurga, S.; Martín-Molina, A.; Vilaseca, E.; Mas, F.; Quesada-Pérez, M. Effect of the surface charge discretization on electric double layers: A Monte Carlo simulation study. J. Chem. Phys. 2007, 126, 234703. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Ma, Y. Monte Carlo determination of mixed electrolytes next to a planar dielectric interface with different surface charge distributions. J. Chem. Phys. 2009, 131, 244715. [Google Scholar] [CrossRef] [PubMed]
- Calero, C.; Faraudo, J. The interaction between electrolyte and surfaces decorated with charged groups: A molecular dynamics simulation study. J. Chem. Phys. 2010, 132, 024704. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y. Impact of head group charges, ionic sizes, and dielectric images on charge inversion: A Monte Carlo simulation study. J. Phys. Chem. B 2010, 114, 13386–13392. [Google Scholar] [CrossRef]
- Vangaveti, S.; Travesset, A. General solution to the electric double layer with discrete interfacial charges. J. Chem. Phys. 2012, 137, 064708. [Google Scholar] [CrossRef] [PubMed]
- Gan, Z.; Xing, X.; Xu, Z. Effects of image charges, interfacial charge discreteness, and surface roughness on the zeta potential of spherical electric double layers. J. Chem. Phys. 2012, 137, 034708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, S. Effects of discreteness of surface charges on the effective electrostatic interactions. J. Chem. Phys. 2014, 140, 234704. [Google Scholar] [CrossRef]
- Bakhshandeh, A.; Frydel, D.; Levin, Y. Charge regulation of colloidal particles in aqueous solutions. Phys. Chem. Chem. Phys. 2020, 22, 24712–24728. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, T.; Wang, X. Structural analysis of confined monovalent salts: Combined effects of steric hindrance, surface charge representation, and dielectric response. Electrochim. Acta 2020, 336, 135707. [Google Scholar] [CrossRef]
- Foret, L.; Kühn, R.; Würger, A. Disjoining pressure of discrete surface charges on thin aqueous films. Phys. Rev. Lett. 2002, 89, 156102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trizac, E.; Hansen, J.P. Wigner–Seitz model of charged lamellar colloidal dispersions. Phys. Rev. E 1997, 56, 3137. [Google Scholar] [CrossRef] [Green Version]
- Kittel, C.; McEuen, P.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1996; Volume 8. [Google Scholar]
- Bossa, G.V.; Bohinc, K.; Brown, M.A.; May, S. Dipole Moment of a Charged Particle Trapped at the Air–Water Interface. J. Phys. Chem. B 2016, 120, 6278–6285. [Google Scholar] [CrossRef] [PubMed]
- Bossa, G.V.; May, S. Integral Representation of Electrostatic Interactions inside a Lipid Membrane. Molecules 2020, 25, 3824. [Google Scholar] [CrossRef]
- Hurd, A.J. The electrostatic interaction between interfacial colloidal particles. J. Phys. A Math. Gen. 1985, 18, L1055. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, P.; Ma, Z. On the physics of both surface overcharging and charge reversal at heterophase interfaces. Phys. Chem. Chem. Phys. 2018, 20, 4118–4128. [Google Scholar] [CrossRef]
- Chang, H.; Ohno, P.E.; Liu, Y.; Lozier, E.H.; Dalchand, N.; Geiger, F.M. Direct Measurement of Charge Reversal on Lipid Bilayers Using Heterodyne-Detected Second Harmonic Generation Spectroscopy. J. Phys. Chem. B 2020, 124, 641–649. [Google Scholar] [CrossRef] [PubMed]
- Frydel, D.; Dietrich, S.; Oettel, M. Charge renormalization for effective interactions of colloids at water interfaces. Phys. Rev. Lett. 2007, 99, 118302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gschwend, G.C.; Girault, H.H. Discrete Helmholtz model: A single layer of correlated counter-ions. Metal oxides and silica interfaces, ion-exchange and biological membranes. Chem. Sci. 2020, 11, 10304–10312. [Google Scholar] [CrossRef]
- Bueno, P.R.; Hein, R.; Santos, A.; Davis, J.J. The nanoscopic principles of capacitive ion sensing interfaces. Phys. Chem. Chem. Phys. 2020, 22, 3770–3774. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bossa, G.V.; May, S. Debye-Hückel Free Energy of an Electric Double Layer with Discrete Charges Located at a Dielectric Interface. Membranes 2021, 11, 129. https://doi.org/10.3390/membranes11020129
Bossa GV, May S. Debye-Hückel Free Energy of an Electric Double Layer with Discrete Charges Located at a Dielectric Interface. Membranes. 2021; 11(2):129. https://doi.org/10.3390/membranes11020129
Chicago/Turabian StyleBossa, Guilherme Volpe, and Sylvio May. 2021. "Debye-Hückel Free Energy of an Electric Double Layer with Discrete Charges Located at a Dielectric Interface" Membranes 11, no. 2: 129. https://doi.org/10.3390/membranes11020129