Trace Metal Modelling of a Complex River Basin Using the Suite of Models Integrated in the OpenMI Platform
Abstract
:1. Introduction
2. Material and Methods
2.1. Trace Metal Dynamics in a Riverine System
2.2. The Study Area
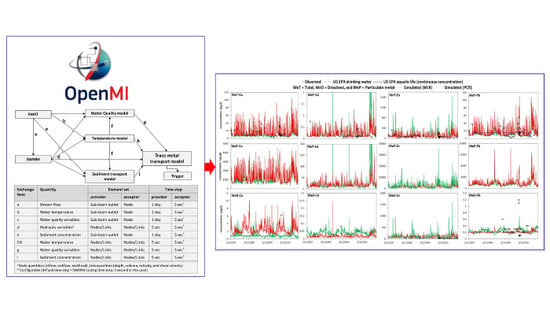
2.3. The Trace Metal Simulator
2.4. Model Inputs, Build up, Calibration and Validation
2.5. Performance Evaluation of the Model
3. Results and Discussion
3.1. The Total Metal Concentrations at The Outlets of Rural Catchment
3.2. The Distribution Coefficients
3.3. The Results of the Integrated Trace Metal Model
3.4. Ecological Status of River Zenne Based on Long Term Simulation Results
3.5. Limitations of the Study
3.6. Usefulness of the OpenMI Platform for Integrated Modelling of a Complex River Basin
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- EU. Directive 2000/60/EC of the European Parliament and of the council of 23 October 2000 establishing a framework for community action in the field of water policy. Off. J. Eur. Communities 2000, L327, 1–72. [Google Scholar]
- EU. Directive 2008/105/EC of the European parliament and of the council of 16 December 2008 on environmental quality standards in the field of water policy, amending and subsequently repealing Council Directives 82/176/EEC, 83/513/EEC, 84/156/EEC, 84/491/EEC, 86/280/EEC and amending Directive 2000/60/EC of the European Parliament and of the Council. Off. J. Eur. Union 2008, L348, 84–97. [Google Scholar]
- Garnier, J.; Brion, N.; Callens, J.; Passy, P.; Deligne, C.; Billen, G.; Servais, P.; Billen, C. Modeling historical changes in nutrient delivery and water quality of the Zenne River (1790s–2010): The role of land use, waterscape and urban wastewater management. J. Mar. Syst. 2012, 128, 62–76. [Google Scholar] [CrossRef]
- Argent, R.M. An overview of model integration for environmental applications—Components, frameworks and semantics. Environ. Model. Softw. 2004, 19, 219–234. [Google Scholar] [CrossRef]
- Mason, A.Z.; Jenkins, K.D. Metal Detoxification in Aquatic Organisms. In Metal Speciation and Bioavailability in Aquatic Systems; Tessier, A., Turner, D.R., Eds.; Wiley & Sons: Chichester, UK, 1995; pp. 469–608. [Google Scholar]
- EU. Directive 2006/44/EC of the European parliament and of the Council of 6 September 2006 on the quality of fresh waters needing protection or improvement in order to support fish life. Off. J. Eur. Union 2006, L264, 20–31. [Google Scholar]
- US-EPA. National Primary Drinking Water Regulations; US EPA: Washington, DC, USA, 2009.
- US-EPA. National Recommended Water Quality Criteria—Aquatic Life Criteria Table. 2017. Available online: https://www.epa.gov/wqc/national-recommended-water-quality-criteria-aquatic-life-criteria-table#table (accessed on 28 February 2018).
- VLAREM. Besluit Milieukwaliteitsnormen Voor Oppervlaktewateren, Waterbodems en Grondwater van 21 mei 2010; Vlaams Reglement betreffende de Milieuvergunning: Brussels, Belgium, 2010.
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2010.
- Gregersen, J.B.; Gijsbers, P.J.A.; Westen, S.J.P. OpenMI: Open modelling interface. J. Hydroinform. 2007, 9, 175–191. [Google Scholar] [CrossRef]
- Moore, R.V.; Tindall, C.I. An overview of the open modelling interface and environment (the OpenMI). Environ. Sci. Policy 2005, 8, 279–286. [Google Scholar] [CrossRef]
- Zhu, Z.; Oberg, N.; Morales, V.M.; Quijano, J.C.; Landry, B.J.; Garcia, M.H. Integrated urban hydrologic and hydraulic modelling in Chicago, Illinois. Environ. Model. Softw. 2016, 77, 63–70. [Google Scholar] [CrossRef]
- Leta, O.T.; Shrestha, N.K.; De Fraine, B.; Bauwens, W. Accessible linking of hydrological and hydraulic models through OpenMI for integrated river basin management. In Water 2011: Integrated Water Resources Management in Tropical and Subtropical Drylands; ILRI: Mekelle, Ethiopia, 2011. [Google Scholar]
- Betrie, G.D.; van Griensven, A.; Mohamed, Y.A.; Popescu, I.; Mynett, A.E.; Hummel, S. Linking SWAT and SOBEK using open modeling interface (OpenMI) for sediment transport simulation in the Blue Nile river basin. Trans. Am. Soc. Agric. Biol. Eng. 2011, 54, 1749–1757. [Google Scholar]
- Shrestha, N.K.; Leta, O.T.; Bauwens, W. Development of RWQM1-based Integrated water quality model in OpenMI with application to the River Zenne, Belgium. Hydrol. Sci. J. 2017, 62, 774–799. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Leta, O.T.; De Fraine, B.; Garcia-Armisen, T.; Ouattara, N.K.; Servais, P.; Van Griensven, A.; Bauwens, W. Modelling Escherichia coli dynamics in the river Zenne (Belgium) using an OpenMI based integrated model. J. Hydroinform. 2014, 16, 354–374. [Google Scholar] [CrossRef]
- Harpham, Q.; Cleverley, P.; Kelly, D. The FluidEarth 2 implementation of OpenMI 2.0. J. Hydroinform. 2014, 16, 890–906. [Google Scholar] [CrossRef]
- Harpham, Q.; Danovaro, E. Towards standard metadata to support models and interfaces in a hydro-meteorological model chain. J. Hydroinform. 2015, 17, 260–274. [Google Scholar] [CrossRef]
- OpenMI. OpenMI Association. 2016. Available online: http://www.openmi.org/ (accessed on 28 February 2018).
- Argent, R.M.; Voinov, A.; Maxwell, T.; Cuddy, S.M.; Rahman, J.M.; Seaton, S.; Vertessy, R.A.; Braddock, R.D. Comparing modelling frameworks—A workshop approach. Environ. Model. Softw. 2006, 21, 895–910. [Google Scholar] [CrossRef]
- Laniak, G.F.; Olchin, G.; Goodall, J.; Voinov, A.; Hill, M.; Glynn, P.; Whelan, G.; Geller, G.; Quinn, N.; Blind, M.; et al. Integrated environmental modeling: A vision and roadmap for the future. Environ. Model. Softw. 2013, 39, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, N.K.; de Fraine, B.; Bauwens, W. SWMM has become OpenMI compliant. In Proceedings of the 9th International Conference on Urban Drainage Modelling; Prodanovic, D., Plavsic, J., Eds.; University of Belgrade: Belgrade, Serbia, 2012. [Google Scholar]
- Tercier-Waeber, M.L.; Taillefert, M. Remote in situ voltammetric techniques to characterize the biogeochemical cycling of trace metals in aquatic systems. J. Environ. Monit. 2008, 10, 30–54. [Google Scholar] [CrossRef] [PubMed]
- Baeyens, W.; van Eck, B.; Lambert, C.; Wollast, R.; Goeyens, L. General description of the Scheldt estuary. Hydrobiologia 1997, 366, 1–14. [Google Scholar] [CrossRef]
- Baeyens, W.; Elskens, M.; Gillain, G.; Goeyens, L. Biogeochemical behaviour of Cd, Cu, Pb and Zn in the Scheldt estuary during the period 1981–1983. Hydrobiologia 1998, 366, 15–44. [Google Scholar] [CrossRef]
- Forstner, U.; Wittman, G.T.W. Metal Pollution in the Aquatic Environment, 2nd ed.; Springer-Verlag: Berlin, Germany, 1981. [Google Scholar]
- Huang, S.L.; Huiwan, Z.; Smith, P. Numerical modeling of heavy metal pollutant transport-transformation in fluvial rivers. J. Hydraul. Res. 2007, 45, 451–461. [Google Scholar] [CrossRef]
- Gao, Y.; Leermakers, M.; Elskens, M.; Billon, G.; Ouddane, B.; Fischer, J.C.; Baeyens, W. High resolution profiles of thallium, manganese and iron assessed by DET and DGT techniques in riverine sediment pore waters. Sci. Total Environ. 2007, 373, 526–533. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Leermakers, M.; Gabelle, C.; Divis, P.; Billon, G.; Ouddane, B.; Fischer, J.C.; Wartel, M.; Baeyens, W. High-resolution profiles of trace metals in the pore waters of riverine sediment assessed by DET and DGT. Sci. Total Environ. 2006, 362, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Lesven, L.; Gillan, D.; Sabbe, K.; Billon, G.; De Galan, S.; Elskens, M.; Baeyens, W.; Leermakers, M. Geochemical behavior of trace elements in sub-tidal marine sediments of the Belgian coast. Mar. Chem. 2009, 117, 88–96. [Google Scholar] [CrossRef]
- Turner, A.; Millward, G.E. Suspended Particles: Their Role in Estuarine Biogeochemical Cycles. Estuar. Coast. Shelf Sci. 2002, 55, 857–883. [Google Scholar] [CrossRef]
- Boyle, J.F.; Birks, H.J.B. Predicting Heavy Metal Concentrations in the Surface Sediments of Norwegian Headwater Lakes from Atmospheric Deposition: An Application of a Simple Sediment-Water Partitioning Model. Water Air Soil Pollut. 1999, 114, 27–51. [Google Scholar] [CrossRef]
- Radovanovic, H.; Koelmans, A.A. Prediction of In Situ Trace Metal Distribution Coefficients for Suspended Solids in Natural Waters. Environ. Sci. Technol. 1998, 32, 753–759. [Google Scholar] [CrossRef]
- US-EPA. Understanding Variation in Partition Coefficients, Kd, Values. In Volume I: The Kd Model, Methods, Measurement and Application of Chemical Reaction Codes; United States Environmental Protection Agency: Washington, DC, USA, 1999; p. 212. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Freundlich, H. Colloid and Cappillary Chemistry; Methuen and Co. Ltd.: London, UK, 1926. [Google Scholar]
- Dubinin, M.M.; Radushkevich, L.V. Equation of the characteristic curve of activated charcoal. Chem. Zentralbl. 1947, 1, 875–890. [Google Scholar]
- Sauve, S.; Hendershot, W.; Allen, H.E. Solid-Solution Partitioning of Metals in Contaminated Soils: Dependence on pH, Total Metal Burden and Organic Matter. Environ. Sci. Technol. 2000, 34, 1125–1131. [Google Scholar] [CrossRef]
- Somlyody, L.; van Straten, G. Modeling and Managing Shallow Lake Eutrophication—With Application to Lake Balaton; Springer-Verlag: Dutch, The Netherlands, 1986. [Google Scholar]
- Reichert, P.; Borchardt, D.; Henze, M.; Rauch, W.; Shanahan, P.; Somlyody, L.; Vanrolleghem, P. River Water Quality Model No. 1, IWA Task Group on River Water Quality Modelling; Scientific & Technical Report No. 12; IWA Publishing: Tokyo, Japan, 2001. [Google Scholar]
- Van Griensven, A. Developments towards integrated water quality modelling for river basins. In Department of Hydrology and Hydraulic Engineering; Vrije Universiteit Brussel: Brussels, Belgium, 2002. [Google Scholar]
- Deligne, C. The rivers of Brussels, 1770–1880: Transformations of an urban landscape. In History of the Urban Environment; Castonguay, S., Ed.; Pittsburgh University Press: Pittsburgh, PA, USA, 2012; pp. 1–15. [Google Scholar]
- Billen, C.; Duvosquel, J.M. Bruxelles; Fonds Mercator: Brussels, Belgium, 2000. [Google Scholar]
- Deligne, C. Bruxelles et sa Rivière: Genèse d'un Territoire Urbain (12e–18e Siècle); Brepols Publishers: Tylenhout, Belgium, 2003. [Google Scholar]
- EU. Directive 91/271/EC. Council directive of 21 May 1991 concening urban waste water treatment. Off. J. Eur. Communities 1991, L135, 40–52. [Google Scholar]
- O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Schawrz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Allen, D.M. The Relationship between Variable Selection and Data Augmentation and a Method for Prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. 1964, 26, 211–243. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Leta, O.T.; De Fraine, B.; Van Griensven, A.; Bauwens, W. OpenMI-based integrated sediment transport modelling of the river Zenne, Belgium. Environ. Model. Softw. 2013, 47, 193–206. [Google Scholar] [CrossRef]
- Mohseni, O.; Stefan, H.G.; Erickson, T.R. A nonlinear regression model for weekly stream temperatures. Water Resour. Res. 1998, 34, 2685–2692. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Leta, O.T.; Nossent, J.; van Griensven, A.; Bauwens, W. Development of a stream water temperature model as a component model for OpenMI based integrated modelling of river Zenne, Belgium. In Proceedings of the 2nd OpenWater Symposium and Workshops, Brussels, Belgium, 16–17 September 2013. [Google Scholar]
- Leta, O.T.; van Griensven, A.; Bauwens, W. Effect of Single and Multisite Calibration Techniques on the Parameter Estimation, Performance and Output of a SWAT Model of a Spatially Heterogeneous Catchment. J. Hydrol. Eng. 2016, 22, 05016036. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nkiaka, E.; Shrestha, N.K.; Leta, O.T.; Bauwens, W. Use of continuous simulation model (COSIMAT) as a complementary tool to model sewer systems: A case study on the Paruck collector, Brussels, Belgium. Water Environ. J. 2016, 30, 310–320. [Google Scholar] [CrossRef]
- Van Griensven, A.; Vandenberghe, V.; Bols, J.; De Pauw, N.; Goethals, P.; Meirlaen, J.; Vanrolleghem, P.A.; Van Vooren, L.; Bauwens, W. Experience and Organisation of Automated Measuring Stations for River Water Quality Monitoring. In Proceedings of the 1st World Congress of the International Water Association, Paris, France, 3–7 July 2000. [Google Scholar]
- Lee, J.Y.; Kim, H.; Kim, Y.; Han, M.Y. Characteristics of the event mean concentration (EMC) from rainfall runoff on an urban highway. Environ. Pollut. 2011, 159, 884–888. [Google Scholar] [CrossRef] [PubMed]
- Birch, G.F.; Richards, R. An integrated source-fate-effects model for sedimentary metals in Sydney estuary and catchment (Australia). In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013. [Google Scholar]
- Rahman, J.M.; Seaton, S.P.; Perraud, J.M.; Hotham, H.; Verrelli, D.I.; Coleman, J.R. It’s TIME for a new environmental modelling framework. In MODSIM 2003: International Congress on Modelling and Simulation; Post, D.A., Ed.; Modelling and Simulation Society of Australia and New Zealand Inc.: Townsville, Australia, 2003; pp. 1727–1732. [Google Scholar]
- Whelan, G.; Castleton, K.J.; Buck, J.W.; Hoopes, B.L.; Pelton, M.A.; Strenge, D.L.; Gelston, G.M.; Kickert, R.N. Concepts of a Framework for Risk Analysis in Multimedia Environmental Systems; Pacific Northwest National Laboratory: Richland, WA, USA, 1997.
- David, O.; Markstrom, S.L.; Rojas, K.W.; Ahuja, L.R.; Schneider, I.W. The object modeling system. In Agricultural Systems Models in Field Research and Technology Transfer; Ahuja, L., Ma, L., Howell, T.A., Eds.; Lewis Publishers, CRC Press LLC: Boca Raton, FL, USA, 2002; pp. 317–331. [Google Scholar]
- Van Ittersum, M.K.; Ewert, F.; Heckelei, T.; Wery, J.; Olsson, J.A.; Andersen, E.; Bezlepkina, I.; Brouwer, F.; Donatelli, M.; Flichman, G.; et al. Integrated assessment of agricultural systems—A component-based framework for the European Union (SEAMLESS). Agric. Syst. 2008, 96, 150–165. [Google Scholar] [CrossRef]
- OpenMI. OpenMI Life Project Website. 2009. Available online: http://www.openmi-life.org/ (accessed on 28 February 2018).
- Helming, K.; Pérez-Soba, M.; Tabbush, P.E. Sustainability Impact Assessment of Land Use Changes; Springer: Berlin, Germany; New York, NY, USA, 2008. [Google Scholar]
- Sutton, M.A.; Reis, S.; Bahl, K.B. Reactive nitrogen in agroecosystems: Integration with greenhouse gas interactions. Agric. Ecosyst. Environ. 2009, 133, 135–138. [Google Scholar] [CrossRef]
- Lindner, M.; Suominen, T.; Palosuo, T.; Garcia-Gonzalo, J.; Verweij, P.; Zudin, S.; Päivinen, R. ToSIA—A tool for sustainability impact assessment of forest-wood-chains. Ecol. Model. 2010, 221, 2197–2205. [Google Scholar] [CrossRef]
- Luoma, S.N. Bioavailability of trace metals to aquatic organisms—A review. Sci. Total Environ. 1983, 28, 1–22. [Google Scholar] [CrossRef]
- Adriano, D.C. Bioavailability of Trace Metals. In Trace Elements in Terrestrial Environments: Biogeochemistry, Bioavailability and Risks of Metals; Adriano, D.C., Ed.; Springer: New York, NY, USA, 2001; pp. 61–89. [Google Scholar]
- Worms, I.A.M.; Slaveykova, V.I.; Wilkinson, K.J. Lead Bioavailability to Freshwater Microalgae in the Presence of Dissolved Organic Matter: Contrasting Effect of Model Humic Substances and Marsh Water Fractions Obtained by Ultrafiltration. Aquat. Geochem. 2015, 21, 217–230. [Google Scholar] [CrossRef]
- Worms, I.A.M.; Adenmatten, D.; Miéville, P.; Traber, J.; Slaveykova, V.I. Photo-transformation of pedogenic humic acid and consequences for Cd(II), Cu(II) and Pb(II) speciation and bioavailability to green microalga. Chemosphere 2015, 138, 908–915. [Google Scholar] [CrossRef] [PubMed]
- Slaveykova, V.I.; Karadjova, I.B.; Karadjov, M.; Tsalev, D.L. Trace Metal Speciation and Bioavailability in Surface Waters of the Black Sea Coastal Area Evaluated by HF-PLM and DGT. Environ. Sci. Technol. 2009, 43, 1798–1803. [Google Scholar] [CrossRef] [PubMed]
- Slaveykova, V.I.; Wilkinson, K.J. Predicting the Bioavailability of Metals and Metal Complexes: Critical Review of the Biotic Ligand Model. Environ. Chem. 2005, 2, 9–24. [Google Scholar] [CrossRef]
- Dedieu, K.; Iuranova, T.; Slaveykova, V.I. Do Exudates Affect Cadmium Speciation and Bioavailability to the Rhizobacterium Sinorhizobium meliloti? Environ. Chem. 2006, 3, 424–427. [Google Scholar] [CrossRef]
- Buahin, C.A.; Horsburgh, J.S. Evaluating the simulation times and mass balance errors of component-based models: An application of OpenMI 2.0 to an urban stormwater system. Environ. Model. Softw. 2015, 72, 92–109. [Google Scholar] [CrossRef]





| Species | Unit | EU WFD | US EPA | Flemish Level # | |
|---|---|---|---|---|---|
| Cd * | total | µg/L | - | 5 c | 8 |
| dissolved | 0.08–0.25 a,† | 0.72 d (1.8 $) | 0.08–0.25 † | ||
| Cu | total | µg/L | - | 1300 c | 30 |
| dissolved | 5–112 b,† | - | 7 | ||
| Pb ** | total | µg/L | - | 15 c | 50 |
| dissolved | 7.2 a | 2.5 d (65 $) | 7.2 | ||
| Zn | total | µg/L | 30–500 b,^, 300–2000 b,^^ | 5000 c | 200 |
| dissolved | - | 120 d,$ | 20 | ||
| Input | Value/Resolution | Remarks/References |
|---|---|---|
| A. SWAT | ||
| Digital Elevation Model (DEM) | 30 × 30 m | ASTER GDEM 1, DHM-OC GIS Vlaanderen |
| Soil map | 20 × 20 m | Carte Numérique des Sols de Wallonie (CNSW) 2, VLM-OC GIS Vlaanderen |
| Landuse map | 20 × 20 m | Corrine (Walloon region), VLM-OC GIS Vlaanderen |
| Hydro-meteorological data (Rainfall, relative humidity, wind speed, solar radiation, temperature) | daily | Royal Meteorological Institute of Belgium (RMI), Direction Générale opérationnelle de la mobilité et des Voies Hydrauliques (DGVH) 3, Vlaamse Milieumaatschappij (VMM) 4 |
| Fertilizer application | Seasonal 5 | Direction Générale Opérationnelle Agriculture, Ressources Naturelles et Environnement (DGARNE) 6, Vlaamse Landmaatschappij (VLM) 7 |
| Point sources | yearly/constant | Société Publique de la Gestion de l’Eau (SPGE) 8 |
| B. SWMM | ||
| River/Canal logitudinal profile and cross section geometry | ca. 100 m | Waterbouwkundig Laboratorium 9 |
| River logitudinal profile and cross section geometry | ca. 100 m | Waterbouwkundig Laboratorium 9 |
| WWTP-Brussels-North sewer system geometry | ca. 100 m | Translated from a hydraulic model HYSTEM-EXTRAN built by Department of Hydrology and Hydraulic Entgineering, Vrije Universiteit Brussel |
| Rainfall | hourly | Royal Meteorological Institute of Belgium (RMI) 10, Société Bruxelloise de Gestion de l’Eau-Brusselse Maatschappij voor Waterbeheer (SBGE/BMWB) 11 |
| Tide levels at outlet | 30 min | Waterbouwkundig Laboratorium 9 |
| Boundary flows at tributaries | daily | SWAT simulated |
| C. Temperature model | ||
| Air temperature | daily | Royal Meteorological Institute of Belgium (RMI) 10 |
| Temperature of WWTP effluent | 20 °C | Constant (Based on GESZ measurements) 12 |
| Temperature of CSO points | 15 °C | Constant (assumed) |
| D. Sediment transport model | ||
| Sediment concentration at tributaries | daily | SWAT simulated |
| Sediment concentration at WWTP outlets | daily | Observed series (Aquiris 13, Vivaqua 14, Aquafin 15) |
| Sediment concentration at CSO points | 207 mg/L | Constant (Based on GESZ measurements) 12 |
| Sediment concentration at outlet | 8.1 mg/L | Constant (Based on GESZ measurements) 12 |
| Particle size distributions, PSDs | - | Based on GESZ measurement 12, constant |
| E. Water Quality model | ||
| Water quality concentration at tributaries | daily | SWAT simulated |
| Water quality concentration at WWTP outlets | weekly | Observed series (Aquiris 13, Vivaqua 14, Aquafin 15) |
| Water quality concentration at CSO points | - | Constant (Based on GESZ measurements) 12 |
| Water quality concentration at river outlet | - | Constant (Based on GESZ measurements) 12 |
| F. Trace metal model | ||
| Trace metal concentration at tributaries | - | Based on MLR and PCA regression |
| Trace metal concentration at WWTP outlets | - | Constant (Based on GESZ measurements) 12 |
| Trace metal concentration at CSO points | - | Constant (Based on GESZ measurements) 12 |
| Trace metal concentration at river outlet | - | Constant (Based on GESZ measurements) 12 |
| Group | Date/Period | Locations | Samples | Remarks |
|---|---|---|---|---|
| Group 1 | 30 September–1 October 2009 | GESZ sampling stations (Z1–Z13), outlets of canals and tributaries, WWTP Brussels South and North. | 16 | During dry weather conditions (DWFs) |
| 26–27 April 2010 | 17 | |||
| 6–7 Jul 2010 | 17 | |||
| 26–27 October 2010 | 17 | |||
| 16–17 September 2010 | GESZ sampling stations (Z4, Z7 and Z9) | 46 | 24-hcampaign | |
| Group 2 | 15–16 December 2009 | Z4 to Z13 | 7 | During dry weather conditions (DWFs) |
| 16 June 2011 | Z9 | 22 | 30-min measurement at wet weather |
| Dependent Variable | Regression Type | Regression Equations | R2 | Press |
|---|---|---|---|---|
| MeT-Cd | MLR | 3 (EC, pH, SPM) 267.72 − 179.48 × EC − 1.35 × pH × SPM + 14.46 × SPM | 0.26 | 328 |
| PCR | 3 (3 components) 0.17 × F3 − 0.32 × F4 − 0.33 × F5 | 0.26 | 76 | |
| MeT-Cu | MLR | 2 (EC, SPM) −2.38 − 22.26 × EC × SPM + 36.61 × SPM | 0.42 | 24 |
| PCR | 9 (7 components) 0.15 × F1 + 0.03 × F1 × F2 − 0.09 × F1 ×F3 − 0.18 × F1 × F5 − 0.07 × F2 + 0.25 × F3 − 0.27 × F4 − 0.39 × F5 − 1.945 × F7 | 0.59 | 58 | |
| MeT-Pb | MLR | 4 (EC, SPM, Ts, pH) 266.7 − 173.2 × EC + 2.36 × SPM + 0.05 × Ts − 0.006 × Ts × pH | 0.42 | 42 |
| PCR | 5 (4 components) 0.1291 × F1 − 0.1698 ×F1 × F5 + 0.2224 × F3 − 0.1538 × F4 − 0.6083 × F5 | 0.46 | 62 | |
| MeT-Zn | MLR | 3 (EC, pH, SPM) 50.76 − 31.99 × EC − 0.31 × pH × SPM + 3.24 × SPM | 0.39 | 8 |
| PCR | 5 (4 components) −0.07031 × F2 × F3 − 0.7675 × F2 × F4 + 0.1849 × F3 − 0.4553 × F4 − 0.3606 × F5 | 0.41 | 68 | |
| LogKd-Cd | MLR | 5 (MeTCd, EC, SO2, SPM) 217.4 − 0.24 × MeTCd − 135.2 × EC + 0.05 × SO2 × MeTCd + 0.17 × SPM × MeTCd | 0.55 | 19 |
| PCR | 7 (5 components) 5.54 + 0.08 × F2 + 0.03 × F2 × F3 + 0.13 × F2 × F7 + 0.14 × F3 − 0.05 × F3 × F6 + 0.21 × F5 − 0.25 × F6 | 0.65 | 17 | |
| LogKd-Cu | MLR | 6 (MeTCu, SO2, pH, SPM) 10.15 − 1.187 × MeTCu + 0.36 × SO2 × SPM − 0.11 × pH × O2 − 2.7 × SPM + 0.91 × SPM × MeTCu | 0.52 | 14 |
| PCR | 11 (7 components) 5.43 − 0.056 × F1 + 0.0098F1 × F2 − 0.094 × F1 × F7 + 0.087 × F2 − 0.109 × F4 + 0.1189 × F5 − 0.0483 × F7 | 0.53 | 15 | |
| LogKd-Pb | MLR | 4 (MeTPb, pH, SPM) 8.46 + 0.26 × pH × SPM − 3.69 × SPM + 0.27 × SPM × MeTPb | 0.49 | 15 |
| PCR | 6 (5 components) 6.04 + 0.05 × F1 + 0.008 × F1 × F2 + 0.05 × F2 + 0.06 × F3-0.12 × F4 + 0.17 × F5 | 0.51 | 16 | |
| LogKd-Zn | MLR | 2 (EC, Ts) 177.62 − 110.9 × EC + 0.002 × Ts × EC | 0.19 | 27 |
| PCR | 11 (7 components) 4.93 + 0.149 × F5 − 0.333 × F6 − 0.368 × F7 − 0.11 × F5 × F6-0.143 × F5 × F7 + 0.176 × F6 × F7 | 0.28 | 25 |
| Variable | Station | Model | Period | Time Span | Obs. | RMSE | MAE | PBIAS (%) | RSR | NSE | Performance Rating # |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Stream flows | Tubize *,*** | SWAT standalone | Cal. | 1998–2008 | 4018 | 1.28 | 0.60 | −7.58 | 0.46 | 0.79 | Very good |
| Val. | 1994–1997 | 1461 | 1.68 | 0.87 | 3.00 | 0.59 | 0.65 | Good | |||
| Lot *** | Integrated | Cal. | 2007–2008 | 731 | 1.45 | 0.79 | −11.39 | 0.53 | 0.72 | Good | |
| Val. | 2009–2010 | 730 | 2.17 | 1.44 | 47.72 | 0.95 | 0.11 | Unsatisfactory | |||
| Vilvoorde *** | Cal. | 2007–2008 | 731 | 1.23 | 0.80 | 0.29 | 0.39 | 0.85 | Very good | ||
| Val. | 2009–2010 | 730 | 2.35 | 1.66 | −3.38 | 0.58 | 0.65 | Good | |||
| Eppegem *** | Cal. | 2007–2008 | 731 | 3.38 | 2.10 | 13.67 | 0.45 | 0.80 | Very good | ||
| Val. | 2009–2010 | 730 | 5.63 | 2.99 | 21.21 | 0.55 | 0.67 | Good | |||
| SPM † | Quenast | SWAT standalone | Cal. | 1998–2008 | 140 | 229.12 | 79.34 | −4.09 | 1.04 | −0.08 | Satisfactory |
| Val. | 1994–1997 | 49 | 121.92 | 52.93 | −11.99 | 1.54 | −1.38 | Satisfactory | |||
| Lot | Integrated | Cal. | 2007–2008 | 22 | 93.82 | 49.61 | 1.41 | 0.81 | 0.34 | Satisfactory | |
| Val. | 2009–2010 | 23 | 123.89 | 43.61 | 13.57 | 1.13 | −0.28 | Satisfactory | |||
| Vilvoorde | Cal. | 2007–2008 | 22 | 68.66 | 47.55 | −14.20 | 1.60 | −1.55 | Satisfactory | ||
| Val. | 2009-2010 | 36 | 87.77 | 45.83 | −6.06 | 1.03 | −0.05 | Satisfactory | |||
| Eppegem | Cal. | 2007–2008 | 22 | 63.28 | 45.09 | −27.31 | 2.31 | −4.32 | Satisfactory | ||
| Val. | 2009–2010 | 36 | 42.63 | 31.54 | −23.69 | 2.20 | −3.86 | Satisfactory | |||
| Ts † | U/S Brussels | Standalone | Cal. | 1990–2010 | 626 | 2.61 | 2.09 | −3.16 | 0.51 | 0.74 | Good |
| Lot | Integrated | Val. | 2007–2010 | 47 | 2.26 | 1.79 | 20.51 | 0.39 | 0.85 | Very good | |
| Vilvoorde | 72 | 1.74 | 1.47 | −10.53 | 0.35 | 0.88 | Very good | ||||
| Eppegem | 75 | 1.47 | 1.25 | −11.78 | 0.3 | 0.91 | Very good | ||||
| DO † | Quenast | SWAT standalone | Cal. | 1998–2008 | 171 | 0.90 | 0.66 | −15.27 | 0.97 | 0.06 | Satisfactory |
| Val. | 1994–1997 | 36 | 2.83 | 2.10 | −25.71 | 1.31 | −0.75 | Unsatisfactory | |||
| GESZ St. | Integrated | Cal. | ** | 13 | 0.86 | 0.72 | −11.46 | 0.86 | 0.26 | Satisfactory | |
| Lot | Val. | 2007–2010 | 45 | 1.44 | 1.20 | 10.63 | 0.61 | 0.63 | Good | ||
| Vilvoorde | 66 | 2.23 | 1.71 | −1.32 | 1.19 | −0.41 | Satisfactory | ||||
| Eppegem | 70 | 2.59 | 2.23 | 47.56 | 1.08 | −0.16 | Unsatisfactory | ||||
| pH † | GESZ St. | Integrated | Cal. | ** | 13 | 0.24 | 0.20 | −2.21 | 2.28 | −4.21 | Satisfactory |
| Lot | Val. | 2007–2010 | 45 | 0.60 | 0.58 | −9.16 | 3.72 | −12.87 | Satisfactory | ||
| Vilvoorde | 70 | 0.26 | 0.20 | −1.32 | 1.19 | −0.41 | Satisfactory | ||||
| Eppegem | 74 | 0.19 | 0.14 | −0.93 | 1.15 | −0.32 | Satisfactory | ||||
| EC † | GESZ St. | Integrated | Cal. | ** | 13 | 142.91 | 88.24 | −0.05 | 0.69 | 0.52 | Good |
| Lot | Val. | 2007–2010 | 46 | 171.05 | 133.20 | 0.17 | 1.32 | −0.74 | Satisfactory | ||
| Vilvoorde | 70 | 334.13 | 218.43 | 0.07 | 1.03 | −0.06 | Satisfactory | ||||
| Eppegem | 73 | 363.58 | 273.97 | −0.05 | 1.02 | −0.03 | Satisfactory | ||||
| MeT-Cu † | Lot | Int.-MLR | Val. | 2007–2010 | 13 | 7.29 | 6.02 | −14.78 | 1.31 | −0.70 | Satisfactory |
| Int.-PCR | 10.49 | 7.30 | −0.44 | 1.24 | −0.53 | Satisfactory | |||||
| Vilvoorde | Int.-MLR | 43 | 14.19 | 10.03 | −2.42 | 0.98 | 0.05 | Satisfactory | |||
| Int.-PCR | 14.42 | 10.17 | −2.38 | 0.94 | 0.11 | Satisfactory | |||||
| Eppegem | Int.-MLR | 41 | 17.49 | 11.61 | 12.41 | 1.28 | −0.65 | Satisfactory | |||
| Int.-PCR | 15.40 | 10.37 | 3.97 | 1.21 | −0.47 | Satisfactory | |||||
| MeT-Cd † | Vilvoorde | Int.-MLR | Val. | 2007–2010 | 23 | 0.31 | 0.25 | 6.19 | 1.20 | −0.45 | Satisfactory |
| Int.-PCR | 0.61 | 0.33 | 16.25 | 1.14 | −0.30 | Satisfactory | |||||
| Eppegem | Int.-MLR | 25 | 0.30 | 0.19 | 25.16 | 1.16 | −0.35 | Satisfactory | |||
| Int.-PCR | 0.28 | 0.18 | 18.94 | 1.21 | −0.45 | Satisfactory | |||||
| MeT-Zn † | Lot | Int.-MLR | Val. | 2007–2010 | 26 | 72.60 | 44.64 | 11.70 | 1.07 | −0.16 | Satisfactory |
| Int.-PCR | 111.05 | 70.38 | 17.81 | 1.69 | −1.86 | Satisfactory | |||||
| Vilvoorde | Int.-MLR | 55 | 78.10 | 50.94 | 3.25 | 0.88 | 0.23 | Satisfactory | |||
| Int.-PCR | 91.12 | 64.27 | 4.93 | 1.13 | −0.27 | Satisfactory | |||||
| Eppegem | Int.-MLR | 49 | 105.68 | 69.60 | 8.65 | 1.31 | −0.71 | Satisfactory | |||
| Int.-PCR | 123.31 | 86.53 | 12.14 | 1.85 | −2.43 | Satisfactory | |||||
| MeT-Pb † | Vilvoorde | Int.-MLR | Val. | 2007–2010 | 55 | 21.97 | 13.00 | 5.98 | 0.86 | 0.26 | Satisfactory |
| Int.-PCR | 21.29 | 12.00 | 2.71 | 0.84 | 0.29 | Satisfactory | |||||
| Eppegem | Int.-MLR | 40 | 20.74 | 15.62 | 9.00 | 1.33 | −0.77 | Satisfactory | |||
| Int.-PCR | 19.00 | 13.82 | 3.19 | 1.26 | −0.59 | Satisfactory | |||||
| MeD-Pb † | Eppegem | Int.-MLR | Val. | 2007–2010 | 24 | 0.28 | 0.16 | 12.57 | 1.01 | −0.01 | Satisfactory |
| Int.-PCR | 0.27 | 0.18 | −2.28 | 1.12 | −0.26 | Satisfactory | |||||
| MeD-Zn † | Vilvoorde | Int.-MLR | Val. | 2007–2010 | 49 | 56.71 | 40.23 | 16.40 | 2.74 | −6.51 | Satisfactory |
| Int.-PCR | 85.74 | 48.41 | 8.26 | 3.05 | −8.32 | Satisfactory | |||||
| Eppegem | Int.-MLR | 30 | 96.04 | 44.59 | 30.28 | 3.46 | −11.00 | Unsatisfactory | |||
| Int.-PCR | 87.59 | 65.43 | 32.67 | 3.98 | −14.82 | Unsatisfactory | |||||
| Performance rating | PBIAS (%) (Stream flow) | PBIAS (%) (Metal) | RSR | NSE | Color Scheme | ||||||
| Very good | <±10 | <±15 | 0 to 0.5 | 0.75 to 1 | |||||||
| Good | ±10 to ±15 | ±15 to ±30 | 0.5 to 0.6 | 0.65 to 0.75 | |||||||
| Satisfactory | ±15 to ±25 | ±30 to ±55 | 0.6 to 0.7 | 0.5 to 0.65 | |||||||
| Unsatisfactory | >±25 | >±55 | >0.7 | <0.5 | |||||||
| Lot | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Metal Species | Flemish 1 | EU WFD 1 | 2007 | 2008 | 2009 | 2010 | ||||
| MLR | PCR | MLR | PCR | MLR | PCR | MLR | PCR | |||
| CdT | 8 | - | 0.16 | 0.17 | 0.21 | 0.48 | 0.22 | 0.23 | 0.34 | 0.68 |
| CdD | 0.09 | 0.09 | 0.003 | 0.014 | 0.002 | 0.015 | 0.002 | 0.012 | 0.002 | 0.013 |
| CuT | 30 | 3.77 | 5.53 | 4.80 | 7.56 | 4.92 | 7.58 | 6.93 | 10.38 | |
| CuD | 7 | 40 | 0.39 | 0.40 | 0.36 | 0.36 | 0.35 | 0.34 | 0.32 | 0.34 |
| PbT | 50 | - | 8.98 | 6.44 | 11.44 | 8.36 | 11.60 | 8.34 | 19.32 | 14.39 |
| PbD | 7.2 | 7.2 | 0.34 | 0.25 | 0.34 | 0.25 | 0.34 | 0.24 | 0.32 | 0.23 |
| ZnT | 200 | 300 | 61.20 | 103.08 | 77.64 | 116.31 | 78.34 | 126.00 | 108.77 | 177.02 |
| ZnD | 20 | - | 22.74 | 47.13 | 19.86 | 21.26 | 19.54 | 27.70 | 20.74 | 23.25 |
| Vilvoorde | ||||||||||
| CdT | 8 | - | 0.15 | 0.14 | 0.17 | 0.26 | 0.18 | 0.18 | 0.24 | 0.33 |
| CdD | 0.09 | 0.09 | 0.008 | 0.023 | 0.009 | 0.027 | 0.009 | 0.027 | 0.010 | 0.030 |
| CuT | 30 | 9.91 | 9.75 | 9.42 | 9.74 | 11.00 | 11.04 | 12.55 | 12.49 | |
| CuD | 7 | 40 | 0.85 | 0.71 | 0.91 | 0.72 | 0.88 | 0.63 | 1.00 | 0.74 |
| PbT | 50 | - | 12.08 | 11.12 | 12.25 | 11.01 | 14.85 | 13.56 | 16.87 | 14.73 |
| PbD | 7.2 | 7.2 | 0.20 | 0.23 | 0.22 | 0.26 | 0.20 | 0.24 | 0.22 | 0.25 |
| ZnT | 200 | 300 | 90.66 | 104.07 | 92.70 | 105.27 | 98.07 | 114.81 | 114.81 | 137.68 |
| ZnD | 20 | - | 60.73 | 59.38 | 63.02 | 60.41 | 62.98 | 66.78 | 73.49 | 77.57 |
| Eppegem | ||||||||||
| CdT | 8 | - | 0.17 | 0.17 | 0.18 | 0.14 | 0.20 | 0.20 | 0.26 | 0.37 |
| CdD | 0.09 | 0.09 | 0.013 | 0.036 | 0.015 | 0.039 | 0.015 | 0.042 | 0.017 | 0.043 |
| CuT | 30 | 14.13 | 10.98 | 13.10 | 10.05 | 14.76 | 11.73 | 15.78 | 13.09 | |
| CuD | 7 | 40 | 2.29 | 1.02 | 2.63 | 0.93 | 2.67 | 0.87 | 2.63 | 1.01 |
| PbT | 50 | - | 15.48 | 13.34 | 14.80 | 11.95 | 16.70 | 14.50 | 18.61 | 15.79 |
| PbD | 7.2 | 7.2 | 0.21 | 0.22 | 0.21 | 0.23 | 0.22 | 0.24 | 0.22 | 0.25 |
| ZnT | 200 | 300 | 92.19 | 162.50 | 91.89 | 122.12 | 99.76 | 143.59 | 115.90 | 166.38 |
| ZnD | 20 | - | 73.52 | 133.15 | 75.27 | 98.91 | 80.52 | 114.44 | 90.39 | 127.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, N.K.; Punzal, C.; Leta, O.T.; Bauwens, W. Trace Metal Modelling of a Complex River Basin Using the Suite of Models Integrated in the OpenMI Platform. Environments 2018, 5, 48. https://doi.org/10.3390/environments5040048
Shrestha NK, Punzal C, Leta OT, Bauwens W. Trace Metal Modelling of a Complex River Basin Using the Suite of Models Integrated in the OpenMI Platform. Environments. 2018; 5(4):48. https://doi.org/10.3390/environments5040048
Chicago/Turabian StyleShrestha, Narayan Kumar, Chrismar Punzal, Olkeba Tolessa Leta, and Willy Bauwens. 2018. "Trace Metal Modelling of a Complex River Basin Using the Suite of Models Integrated in the OpenMI Platform" Environments 5, no. 4: 48. https://doi.org/10.3390/environments5040048