Micromechanical Modeling for Predicting Residual Stress–Strain State around Nodules in Ductile Cast Irons
Abstract
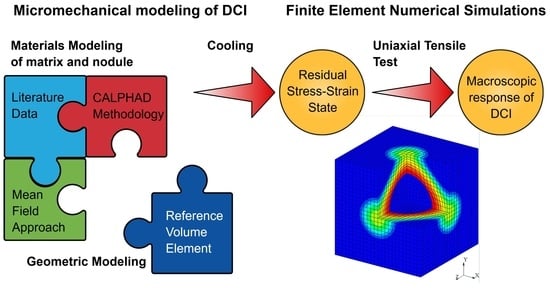
:1. Introduction
2. Material and Constitutive Modeling
2.1. DCI
2.2. Matrix
2.2.1. Microstructure
2.2.2. Mechanical Properties
2.3. Nodules
3. Numerical Modeling
4. Simulations and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A





References
- Zanardi, F.; Mapelli, C.; Barella, S. Reclassification of Spheroidal Graphite Ductile Cast Irons Grades According to Design Needs. Int. J. Met. 2020, 14, 622–655. [Google Scholar] [CrossRef]
- Bai, J.; Xu, H.; Wang, Y.; Chen, X.; Zhang, X.; Cao, W.; Xu, Y. Microstructures and Mechanical Properties of Ductile Cast Iron with Different Crystallizer Inner Diameters. Crystals 2022, 12, 413. [Google Scholar] [CrossRef]
- Riposan, I.; Anca, D.; Stan, I.; Chisamera, M.; Stan, S. Graphite Nodularity Evaluation in High-Si Ductile Cast Irons. Materials 2022, 15, 7685. [Google Scholar] [CrossRef] [PubMed]
- Stan, I.; Anca, D.; Stan, S.; Riposan, I. Solidification pattern of si-alloyed, inoculated ductile cast irons, evaluated by thermal analysis. Metals 2021, 11, 846. [Google Scholar] [CrossRef]
- Iacoviello, F.; Di Cocco, V.; Bellini, C. Overload effects on fatigue cracks in a ferritized ductile cast iron. Int. J. Fatigue 2019, 127, 376–381. [Google Scholar] [CrossRef]
- Iacoviello, F.; Di Cocco, V.; Bellini, C. Fatigue crack propagation and damaging micromechanisms in Ductile Cast Irons. Int. J. Fatigue 2019, 124, 48–54. [Google Scholar] [CrossRef]
- Chaus, A.S.; Čaplovič, Ľ.; Pokrovskii, A.I.; Sobota, R. Microstructure and Properties Evaluation of Ductile Cast Iron Subjected To Hot Plastic Deformation and Ambient Temperature Compression. Arch. Metall. Mater. 2023, 68, 639–648. [Google Scholar] [CrossRef]
- Galkin, V.; Kurkin, A.; Gavrilov, G.; Kulikov, I.; Bazhenov, E. Investigation of the Technological Possibility of Manufacturing Volumetric Shaped Ductile Cast Iron Products in Open Dies. Materials 2023, 16, 274. [Google Scholar] [CrossRef]
- Collini, L.; Pirondi, A. Micromechanical modeling of the effect of stress triaxiality on the strain to failure of ductile cast iron. Eng. Fract. Mech. 2020, 238, 107270. [Google Scholar] [CrossRef]
- Keough, J.R.; Hayrynen, K.L.; Pioszak, G.L. Designing with Austempered Ductile Iron (ADI). Proc. Trans. Am. Foundry Soc. 2010, 118, 503–517. [Google Scholar]
- Zanardi, F.; Bonollo, F.; Angella, G.; Bonora, N.; Iannitti, G.; Ruggiero, A. A contribution to new material standards for ductile irons and austempered ductile irons. Int. J. Met. 2017, 11, 136–147. [Google Scholar] [CrossRef]
- Brocks, W.; Hao, S.; Steglich, D. Micromechanical modelling of the damage and toughness behaviour of nodular cast iron materials. J. Phys. IV JP 1996, 6, C6-43–C6-52. [Google Scholar] [CrossRef]
- Steglich, D.; Brocks, W. Micromechanical modelling of the behaviour of ductile materials including particles. Comput. Mater. Sci. 1997, 9, 7–17. [Google Scholar] [CrossRef]
- Bonora, N.; Ruggiero, A. Micromechanical modeling of ductile cast iron incorporating damage. Part I: Ferritic ductile cast iron. Int. J. Solids Struct. 2005, 42, 1401–1424. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Hattel, J. Modeling the elastic behavior of ductile cast iron including anisotropy in the graphite nodules. Int. J. Solids Struct. 2016, 100–101, 523–535. [Google Scholar] [CrossRef]
- Pereira, A.; Costa, M.; Anflor, C.; Pardal, J.; Leiderman, R. Estimating the effective elastic parameters of nodular cast iron from micro-tomographic imaging and multiscale finite elements: Comparison between numerical and experimental results. Metals 2018, 8, 695. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Andriollo, T.; Fæster, S.; Liu, W.; Hattel, J.; Barabash, R.I. Three-dimensional local residual stress and orientation gradients near graphite nodules in ductile cast iron. Acta Mater. 2016, 121, 173–180. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Andriollo, T.; Fæster, S.; Barabash, R.; Xu, R.; Tiedje, N.; Thorborg, J.; Hattel, J.; Juul Jensen, D.; Hansen, N. Microstructure and residual elastic strain at graphite nodules in ductile cast iron analyzed by synchrotron X-ray microdiffraction. Acta Mater. 2019, 167, 221–230. [Google Scholar] [CrossRef]
- Krasowsky, A.J.; Kramarenko, I.V.; Kalaida, V.V. Fracture toughness of nodular graphite cast irons under static, impact and cyclic loading. Fatigue Fract. Eng. Mater. Struct. 1987, 10, 223–237. [Google Scholar] [CrossRef]
- Iannitti, G.; Ruggiero, A.; Bonora, N.; Masaggia, S.; Veneri, F. Micromechanical modelling of constitutive behavior of austempered ductile iron (ADI) at high strain rate. Theor. Appl. Fract. Mech. 2017, 92, 351–359. [Google Scholar] [CrossRef]
- Andriollo, T.; Zhang, Y.; Fæster, S.; Thorborg, J.; Hattel, J. Impact of micro-scale residual stress on in-situ tensile testing of ductile cast iron: Digital volume correlation vs. model with fully resolved microstructure vs. periodic unit cell. J. Mech. Phys. Solids 2019, 125, 714–735. [Google Scholar] [CrossRef]
- Andriollo, T.; Hellström, K.; Sonne, M.R.; Thorborg, J.; Tiedje, N.; Hattel, J. Uncovering the local inelastic interactions during manufacture of ductile cast iron: How the substructure of the graphite particles can induce residual stress concentrations in the matrix. J. Mech. Phys. Solids 2018, 111, 333–357. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams: With Special Reference to Refractory Metals; Academic Press Inc.: New York, NY, USA, 1970; Volume 4, p. 344. [Google Scholar]
- Saunders, N.; Guo, Z.; Li, X.; Miodownik, A.P.; Schillé, J.P. Using JMatPro to model materials properties and behavior. Jom 2003, 55, 60–65. [Google Scholar] [CrossRef]
- Ductile Iron Society. Ductile Iron Data for Design Engineers; Ductile Iron Society: Germantown, WI, USA, 1990. [Google Scholar]
- American Foundrymen’s Society. Ductile Iron Handbook; American Foundrymen’s Society: Des Plaines, IL, USA, 1993; p. 277. [Google Scholar]
- Andriollo, T.; Thorborg, J.; Tiedje, N.; Hattel, J. A micro-mechanical analysis of thermo-elastic properties and local residual stresses in ductile iron based on a new anisotropic model for the graphite nodules. Model. Simul. Mater. Sci. Eng. 2016, 24, 55012. [Google Scholar] [CrossRef]
- Kohout, J. A simple relation for deviation of grey and nodular cast irons from Hooke’s law. Mater. Sci. Eng. A 2001, 313, 16–23. [Google Scholar] [CrossRef]
- Angus, H.T. Cast Iron: Physical and Engineering Properties; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar] [CrossRef]
- Speich, G.R.; Schwoeble, A.J.; Kapadia, B.M. Elastic moduli of gray and nodular cast iron. J. Appl. Mech. Trans. ASME 1980, 47, 821–826. [Google Scholar] [CrossRef]
- Hervas, I. Contribution à l’Étude des Mécanismes d’Endommagement des Fontes Ferritiques à Graphite Sphéroïdal: Influence de la Température, du Trajet de Chargement et rôle des Interfaces Nodules/Matrice. Ph.D. Thesis, University of Caen Normandy, Caen, France, 2013. [Google Scholar]
- Kuna, M.; Sun, D.Z. Three-dimensional cell model analyses of void growth in ductile materials. Int. J. Fract. 1996, 81, 235–258. [Google Scholar] [CrossRef]
- Sherby, O.D.; Burke, P.M. Mechanical behavior of crystalline solids at elevated temperature. Prog. Mater. Sci. 1968, 13, 323–390. [Google Scholar] [CrossRef]
- Esposito, L.; Bonora, N. A primary creep model for Class M materials. Mater. Sci. Eng. A 2011, 528, 5496–5501. [Google Scholar] [CrossRef]
- Mukherjee, A.K.; Bird, J.E.; Dorn, J.E. Experimental Correlations for High-Temperature Creep; Technical Report; University of California, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1968. [Google Scholar]
- Bird, J.; Mukherjee, A.; Dorn, J.E. Correlations between High-Temperature Creep Behavior and Structure; Technical Report; University of California, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1969. [Google Scholar]
- Lagneborg, R.; Bergman, B. The stress/creep rate behaviour of precipitation-hardened alloys. Met. Sci. 1976, 10, 20–28. [Google Scholar] [CrossRef]
- Evans, W.J.; Harrison, G.F. The development of a universal equation for secondary creep rates in pure metals and engineering alloys. Met. Sci. 1976, 10, 307–313. [Google Scholar] [CrossRef]
- Davies, P.W.; Nelmes, G.; Williams, K.R.; Wilshire, B. Stress-change experiments during high-temperature creep of copper, iron, and zInc. Met. Sci. J. 1973, 7, 87–92. [Google Scholar] [CrossRef]
- Parker, J.D.; Wilshire, B. The Effect of a Dispersion of Cobalt Particles on High-Temperature Creep of Copper. Met. Sci. 1975, 9, 248–252. [Google Scholar] [CrossRef]
- Lund, R.W.; Nix, W.D. High temperature creep of Ni-20Cr-2ThO2 single crystals. Acta Metall. 1976, 24, 469–481. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Kazakulov, I. Deformation behavior of Fe - 3Si steel. Mater. Sci. Technol. 2004, 20, 221–228. [Google Scholar] [CrossRef]
- Barrett, C.R. The Influence of Grain Boundaries and Stacking Faults on High Temperature Plastic Deformation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1964. [Google Scholar]
- Stang, R.G.; Nix, W.D.; Barrett, C.R. High temperature creep in Fe-3 pct Si. Metall. Trans. 1973, 4, 1695–1699. [Google Scholar] [CrossRef]
- Stang, R.G.; Nix, W.D.; Barrett, C.R. The influence of subgrain boundaries on the rate controlling creep processes in Fe-3 Pct Si. Metall. Trans. A 1975, 6, 2065–2071. [Google Scholar] [CrossRef]
- Mohamed, F.A.; Park, K.T.; Lavernia, E.J. Creep behavior of discontinuous SiC-Al composites. Mater. Sci. Eng. A 1992, 150, 21–35. [Google Scholar] [CrossRef]
- Madelung, O. (Ed.) Diffusion in Solid Metals and Alloys; Springer: Berlin/Heidelberg, Germany, 1990; Volume 26. [Google Scholar] [CrossRef]
- Cottrell, A. An Introduction to Metallurgy; The Institute of Materials: London, UK, 1995; p. 548. [Google Scholar]
- Frost, H.J.; Ashby, M.F. Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, 1st ed.; Pergamon Press: Oxford, UK; New York, NY, USA, 1982; p. 166. [Google Scholar]
- Cadek, J. Creep in Metallic Materials; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1988; Volume 48. [Google Scholar]
- Hervas, I.; Bettaieb, M.B.; Thuault, A.; Hug, E. Graphite nodule morphology as an indicator of the local complex strain state in ductile cast iron. Mater. Des. 2013, 52, 524–532. [Google Scholar] [CrossRef]
- Colonna, F.; Los, J.H.; Fasolino, A.; Meijer, E.J. Properties of graphite at melting from multilayer thermodynamic integration. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 80, 1–8. [Google Scholar] [CrossRef]
- Delprete, C.; Sesana, R. Experimental characterization of a Si-Mo-Cr ductile cast iron. Mater. Des. 2014, 57, 528–537. [Google Scholar] [CrossRef]
- Tsang, D.K.; Marsden, B.J.; Fok, S.L.; Hall, G. Graphite thermal expansion relationship for different temperature ranges. Carbon 2005, 43, 2902–2906. [Google Scholar] [CrossRef]
- Riley, D. The thermal expansion of graphite: Part II. Theoretical. Proc. Phys. Soc. 1945, 57, 486. [Google Scholar] [CrossRef]
- Monchoux, J.P.; Verdu, C.; Thollet, G.; Fougères, R.; Reynaud, A. Morphological changes of graphite spheroids during heat treatment of ductile cast irons. Acta Mater. 2001, 49, 4355–4362. [Google Scholar] [CrossRef]
- MSC Software Corporation. MSC Marc Volume A: Theory and User Information; MSC Software Corporation: Newport Beach, CA, USA, 2019. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Andriollo, T.; Fæster, S.; Winther, G. Probing the structure and mechanical properties of the graphite nodules in ductile cast irons via nano-indentation. Mech. Mater. 2018, 122, 85–95. [Google Scholar] [CrossRef]
- Levine, L.E.; Okoro, C.; Xu, R. Full elastic strain and stress tensor measurements from individual dislocation cells in copper through-Si vias. IUCrJ 2015, 2, 635–642. [Google Scholar] [CrossRef]






















| C | Si | Mn | P | S | Cr | Ni | Co | Cu | Ti | V | Mg | Ce | Se |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.68 | 2.30 | 0.22 | 0.015 | 0.011 | 0.027 | 0.048 | 0.024 | 0.016 | 0.017 | 0.014 | 0.11 | 0.042 | 0.043 |
| Vol.% | Wt.% | |
|---|---|---|
| Graphite | 11.207 | 3.591 |
| Ferrite | 87.827 | 95.362 |
| Cementite | 0.966 | 1.048 |
| C | Si | Mn | P | S | Cr | Ni | Co | Cu | Ti | V | Mg | Ce | Se |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.058 | 2.386 | 0.228 | 0.016 | 0.011 | 0.028 | 0.05 | 0.025 | 0.017 | 0.018 | 0.015 | 0.114 | 0.044 | 0.045 |
| wt.% | Vol.% | |
|---|---|---|
| Ferrite | 99.217 | 99.165 |
| Cementite | 0.71308 | 0.717 |
| M6C | 0.03939 | 0.06003 |
| MNS | 0.03093 | 0.05863 |
| B | (KJ/mol) | (m2/s) | Q (KJ/mol) | n | A | ||
|---|---|---|---|---|---|---|---|
| 5.69 × 10 | 46.1 | 2 × | 280 | 4.75 | 7.9090 × | 8.16 | 3.3390 × |
(mm/mm) | (MPa) | m3/mole | m3/mole | (MPa) |
|---|---|---|---|---|
| 2.2515 × | 4.7957 × | × | × | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruggiero, A.; Khademi, E. Micromechanical Modeling for Predicting Residual Stress–Strain State around Nodules in Ductile Cast Irons. Metals 2023, 13, 1874. https://doi.org/10.3390/met13111874
Ruggiero A, Khademi E. Micromechanical Modeling for Predicting Residual Stress–Strain State around Nodules in Ductile Cast Irons. Metals. 2023; 13(11):1874. https://doi.org/10.3390/met13111874
Chicago/Turabian StyleRuggiero, Andrew, and Ehsan Khademi. 2023. "Micromechanical Modeling for Predicting Residual Stress–Strain State around Nodules in Ductile Cast Irons" Metals 13, no. 11: 1874. https://doi.org/10.3390/met13111874