Predicting Cyanide Consumption in Gold Leaching: A Kinetic and Thermodynamic Modeling Approach
Abstract
:1. Introduction
2. Theory
3. Methodology
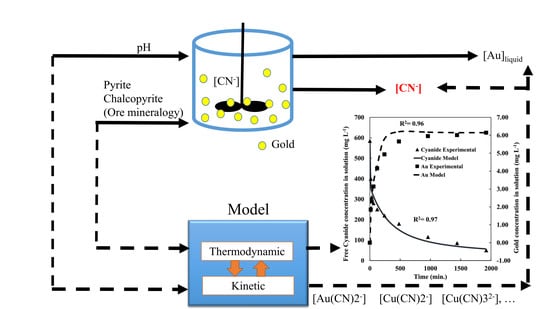
3.1. Leaching Modeling
3.2. Speciation Modeling
3.3. Integrated Modeling of Leaching Kinetics and Chemical Speciation with MATLAB
3.4. Experimental
3.5. Model Calibration
4. Results and Discussion
4.1. Pyrite Leaching
4.2. Chalcopyrite Leaching
4.3. Pyrite + Chalcopyrite Leaching
4.4. Gold + Pyrite + Chalcopyrite Leaching
4.5. Gold + Pyrite + Chalcopyrite + Quartz Leaching
4.6. Cross Validation: Effect of pH
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marsden, J.; House, I. The Chemistry of Gold Extraction, 2nd ed.; SME: Littleton, CO, USA, 2006. [Google Scholar]
- Riveros, P.A. Selectivity aspects of the extraction of gold from cyanide solutions with ion exchange resins. Hydrometallurgy 1993, 33, 43–58. [Google Scholar] [CrossRef]
- Anderson, C.G. Alkaline sulfide gold leaching kinetics. Miner. Eng. 2016, 92, 248–256. [Google Scholar] [CrossRef]
- Muir, D. A review of the selective leaching of gold from oxidised copper-old ores with ammonia-cyanide and new insights for plant control and operation. Miner. Eng. 2011, 24, 576–582. [Google Scholar] [CrossRef]
- Khodadadi, A.; Teimoury, P.; Abdollahy, M.; Samiee, A. Detoxification of cyanide in a gold processing plant tailings water using calcium and sodium hypochlorite. Mine Water Environ. 2008, 27, 52–55. [Google Scholar] [CrossRef]
- Kuyucak, N.; Akcil, A. Cyanide and removal options from effluents in gold mining and metallurgical processes. Miner. Eng. 2013, 50, 13–29. [Google Scholar] [CrossRef]
- Deschenes, G.; Wallingford, G. Effect of oxygen and lead nitrate on the cyanidation of a sulphide bearing gold ore. Miner. Eng. 1995, 8, 923–931. [Google Scholar] [CrossRef]
- De Andrade Lima, L.; Hodouin, D. A lumped kinetic model for gold ore cyanidation. Hydrometallurgy 2005, 79, 121–137. [Google Scholar] [CrossRef]
- Adams, M. The chemical behaviour of cyanide in the extraction of gold. 1. Kinetics of cyanide loss in the presence and absence of activated carbon. J. S. Afr. Inst. Min. Metall. 1990, 90, 37–44. [Google Scholar]
- Adams, M. The chemical behaviour of cyanide in the extraction of gold. 2. Mechanisms of cyanide loss in the carbon-in-pulp process. J. S. Afr. Inst. Min. Metall. 1990, 90, 67–73. [Google Scholar]
- Bellec, S.; Hodouin, D.; Bazin, C.; Khalesi, M.; Duchesne, C. Modelling and simulation of gold ore leaching. In Proceedings of the World Gold Conference, Gauteng, South Africa, 26–30 October 2009; pp. 51–60. [Google Scholar]
- Adams, M. A methodology for determining the deportment of cyanide losses in gold plants. Miner. Eng. 2001, 14, 383–390. [Google Scholar] [CrossRef]
- Lotz, P.; Janse van Rensburg, S.; Swarts, A. Kinetic gold leach monitoring including cyanide speciation. J. S. Afr. Inst. Min. Metall. 2009, 109, 635–639. [Google Scholar]
- Zhang, Y.; Fang, Z.; Muhammed, M. On the solution chemistry of cyanidation of gold and silver bearing sulphide ores. A critical evaluation of thermodynamic calculations. Hydrometallurgy 1997, 46, 251–269. [Google Scholar] [CrossRef]
- Lu, J.; Dreisinger, D.; Cooper, W. Thermodynamics of the aqueous copper-cyanide system. Hydrometallurgy 2002, 66, 23–36. [Google Scholar] [CrossRef]
- Luthy, R.G.; Bruce, S.G., Jr. Kinetics of reaction of cyanide and reduced sulfur species in aqueous solution. Environ. Sci. Technol. 1979, 13, 1481–1487. [Google Scholar] [CrossRef]
- Oraby, E.; Eksteen, J. Gold dissolution and copper suppression during leaching of copper-gold gravity concentrates in caustic soda-low free cyanide solutions. Miner. Eng. 2016, 87, 10–17. [Google Scholar] [CrossRef]
- Breuer, P.; Dai, X.; Jeffrey, M. Leaching of gold and copper minerals in cyanide deficient copper solutions. Hydrometallurgy 2005, 78, 156–165. [Google Scholar] [CrossRef]
- Kyle, J.H.; Hefter, G. A critical review of the thermodynamics of hydrogen cyanide and copper(I)-cyanide complexes in aqueous solution. Hydrometallurgy 2015, 154, 78–87. [Google Scholar] [CrossRef]
- Lukey, G.; Van Deventer, J.; Chowdhury, R.; Shallcross, D. The effect of salinity on the capacity and selectivity of ion exchange resins for gold cyanide. Miner. Eng. 1999, 12, 769–785. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C. User’s Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey: Reston, VA, USA, 1999.
- Vítková, M.; Ettler, V.; Šebek, O.; Mihaljevič, M.; Grygar, T.; Rohovec, J. The pH-dependent leaching of inorganic contaminants from secondary lead smelter fly ash. J. Hazard. Mater. 2009, 167, 427–433. [Google Scholar] [CrossRef] [PubMed]
- Martens, E.; Jacques, D.; Van Gerven, T.; Wang, L.; Mallants, D. PHREEQC modelling of leaching of major elements and heavy metals from cementitious waste forms. In Materials Research Society Symposia Proceedings; Cambridge University Press: Cambridge, UK, 2008; p. 475. [Google Scholar]
- Halim, C.E.; Short, S.A.; Scott, J.A.; Amal, R.; Low, G. Modelling the leaching of Pb, Cd, As, and Cr from cementitious waste using PHREEQC. J. Hazard. Mater. 2005, 125, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Tiruta-Barna, L. Using PHREEQC for modelling and simulation of dynamic leaching tests and scenarios. J. Hazard. Mater. 2008, 157, 525–533. [Google Scholar] [CrossRef] [PubMed]
- Peterson, S.; Hostetler, C.; Deutsch, W.; Cowan, C. MINTEQ User’s Manual; Pacific Northwest Lab.: Richland, WA, USA; Division of Waste Management, Nuclear Regulatory Commission: Washington, DC, USA, 1987.
- Smith, R.M.; Martell, A.E. Critical Stability Constants; Plenum Press: New York, NY, USA, 1976; Volume 4. [Google Scholar]
- Schweitzer, G.K.; Pesterfield, L.L. The Aqueous Chemistry of the Elements; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Akilan, C.; Königsberger, E.; Solis, J.S.; May, P.M.; Kyle, J.H.; Hefter, G. Investigation of complexation and solubility equilibria in the copper(I)/cyanide system at 25 °C. Hydrometallurgy 2016, 164, 202–207. [Google Scholar] [CrossRef]
- Paz-García, J.M.; Johannesson, B.; Ottosen, L.M.; Ribeiro, A.B.; Rodríguez-Maroto, J.M. Computing multi-species chemical equilibrium with an algorithm based on the reaction extents. Comput. Chem. Eng. 2013, 58, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Strong, B.; Murray-Smith, R. Determination of gold in copper-bearing sulphide ores and metallurgical flotation products by atomic-absorption spectrometry. Talanta 1974, 21, 1253–1258. [Google Scholar] [CrossRef]
- Breuer, P.; Sutcliffe, C.; Meakin, R. Cyanide measurement by silver nitrate titration: Comparison of rhodanine and potentiometric end-points. Hydrometallurgy 2011, 106, 135–140. [Google Scholar] [CrossRef]
- Adams, M. The removal of cyanide from aqueous solution by the use of ferrous sulphate. J. S. Afr. Inst. Min. Metall. 1992, 92, 17–25. [Google Scholar]
- Xie, F.; Dreisinger, D.B. Use of ferricyanide for gold and silver cyanidation. Trans. Nonferr. Met. Soc. China 2009, 19, 714–718. [Google Scholar] [CrossRef]
- Xie, F.; Dreisinger, D.; Lu, J. The novel application of ferricyanide as an oxidant in the cyanidation of gold and silver. Miner. Eng. 2008, 21, 1109–1114. [Google Scholar] [CrossRef]
- Khalesi, M.; Bazin, C.; Hodouin, D.; Bellec, S. Modelling of the gold content within the size intervals of a grinding mill product. In Proceedings of the World Gold Conference, Montreal, QC, Canada, 2–5 October 2011; pp. 437–450. [Google Scholar]
- Khalesi, M.; Bazin, C.; Hodouin, D.; Bellec, S. A liberation model for the integrated simulation of grinding and leaching of gold ore. In Proceedings of the World Gold Conference, Gauteng, South Africa, 26–30 October 2009; pp. 61–73. [Google Scholar]
- Kianinia, Y.; Khalesi, M.; Abdollahy, M.; Darban, A.K. Modeling the cyanide consumption in leaching of gold ores based on the amount and liberation degree of cyanicides. Can. Metall. Q. 2017, in press. [Google Scholar]
- Kondos, P.D.; Deschênes, G.; Morrison, R.M. Process optimization studies in gold cyanidation. Hydrometallurgy 1995, 39, 235–250. [Google Scholar] [CrossRef]










| Equilibrium | log K | Ref. |
|---|---|---|
| CN− + H+ = HCN | 9.21 | [14,19] |
| Au+ + 2CN− = Au(CN)2− | 39.3 | [2,27] |
| H2O = H+ + OH− | −13.98 | [14] |
| Au+ + CN− = AuCN(s) | 38.9 | [14] |
| Fe2+ + 6CN− = Fe(CN)64− | 35.4 | [14] |
| S + CN− = SCN− | 0.9 | [28] |
| ½O2 + CN− = OCN− | 3.5 | [28] |
| Cu+ + 2CN− = Cu(CN)2− | 23.7 | [29] |
| Cu+ + 3CN− = Cu(CN)32− | 28.5 | [29] |
| Cu+ + 4CN− = Cu(CN)43− | 30.6 | [29] |
| Cu2+ + 2H2O = Cu(OH)2 + 2H+ | −16.24 | [14] |
| Fe2+ + 3H2O = Fe(OH)3− + 3H+ | −32 | [14] |
| Fe3+ + 2H2O = FeOOH + 3H+ | −0.5 | [14] |
| Cu(CN)2− = CuCN(s) + CN− | −4.91 | [14] |
| Mineral | Elemental Composition (wt %) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zn | Si | Sb | S | Pb | Fe | Cu | Ca | As | Al | |
| Chalcopyrite | 0.26 | 2.86 | 0.02 | 33.44 | 0.01 | 29.26 | 33.18 | 0.01 | 0.012 | 0.01 |
| Pyrite | 0.01 | 0.19 | 0.02 | 52.71 | 0.02 | 46.13 | 0.02 | 0.01 | 0.01 | 0.19 |
| System * | Mineral | k ** | α | β |
|---|---|---|---|---|
| Py. | Py. | 6.8 | 1.01 | 1.1 |
| Ch. | Ch. | 0.58 | 0.86 | 1.15 |
| Py. + Ch. | Py. | 4.71 | 0.31 | 1.82 |
| Ch. | 0.62 | 0.61 | 1.16 | |
| Au + Py. + Ch. (±Qtz.) | Py. | 5.96 | 0.28 | 2.14 |
| Ch. | 0.73 | 0.71 | 1.25 | |
| Au | 14.99 | 0.91 | 1.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kianinia, Y.; Khalesi, M.R.; Abdollahy, M.; Hefter, G.; Senanayake, G.; Hnedkovsky, L.; Khodadadi Darban, A.; Shahbazi, M. Predicting Cyanide Consumption in Gold Leaching: A Kinetic and Thermodynamic Modeling Approach. Minerals 2018, 8, 110. https://doi.org/10.3390/min8030110
Kianinia Y, Khalesi MR, Abdollahy M, Hefter G, Senanayake G, Hnedkovsky L, Khodadadi Darban A, Shahbazi M. Predicting Cyanide Consumption in Gold Leaching: A Kinetic and Thermodynamic Modeling Approach. Minerals. 2018; 8(3):110. https://doi.org/10.3390/min8030110
Chicago/Turabian StyleKianinia, Yaser, Mohammad Reza Khalesi, Mahmoud Abdollahy, Glenn Hefter, Gamini Senanayake, Lubomir Hnedkovsky, Ahmad Khodadadi Darban, and Marjan Shahbazi. 2018. "Predicting Cyanide Consumption in Gold Leaching: A Kinetic and Thermodynamic Modeling Approach" Minerals 8, no. 3: 110. https://doi.org/10.3390/min8030110