Investigating the Performance of a Fractal Ultrasonic Transducer Under Varying System Conditions
Abstract
:1. Introduction
2. Fractal Transducer Design
3. Mathematical Model for the Fractal Transducer
4. Investigating the Robustness of Transducer Performance
4.1. Transducer Performance with Uncertainty in the Key Material Parameters
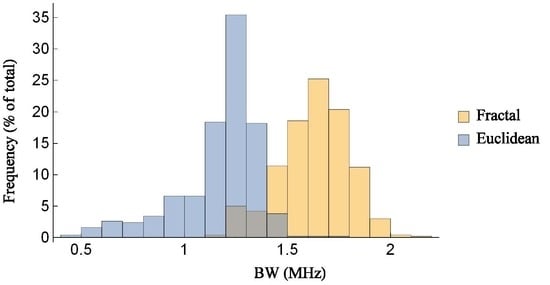
4.2. Transducer Performance under Various Design Regimes
4.3. Transducer Performance under Various Design Regimes with Uncertainty in Material Parameter Values
4.4. Discussion of Transducer Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Matrix used to construct | |
| Cross-sectional area of each edge of the Sierpinski gasket transducer (m) | |
| a | (ratio of electrical impedances in the circuit (non-dimensional)) |
| b | (ratio of electrical impedances in the circuit (Ω)) |
| The capacitance of the transducer (F) | |
| An element of the stiffness tensor of the piezoelectric material (N·m) | |
| The (piezoelectrically stiffened) wave velocity in the SG lattice (m·s) | |
| Wave speed in the front load (m·s) | |
| Wave speed in the backing layer (m·s) | |
| An element of the piezoelectric tensor of the piezoelectric material (C·m or N·V·m) | |
| f | The natural frequency |
| The Green’s transfer matrix given by Equation (1)–Equation (4) (non-dimensional) | |
| Recursive relations utilised for the renormalisation approach, given by Equation (7) and Equation (8) (non-dimensional) | |
| h | Length of each edge of the Sierpinski gasket transducer (m) |
| Non-dimensionalised parameter given by Equation (12) | |
| L | Thickness of transducer (m) |
| m | The vertex labelled |
| The total number of vertices in the SG lattice | |
| n | The fractal generation level |
| q | Scaled frequency |
| Mechanical impedance of backing layer (N·s·m) | |
| Mechanical impedance of the front load (N·s·m) | |
| Mechanical impedance of the transducer (N·s·m) | |
| Parallel circuit electrical impedance load (Ω) | |
| Series circuit electrical impedance load (Ω) | |
| Electrical impedance of the SG lattice given by Equation (11) (Ω) | |
| α | Non-dimensionalised parameter equal to |
| β | Non-dimensionalised parameter equal to |
| Non-dimensionalised parameter given by Equation (5) | |
| Non-dimensionalised parameter equal to | |
| Element of the permittivity tensor of the piezoelectric material (F·m) | |
| ζ | (V·m) |
| Non-dimensionalised parameter given by Equation (6) | |
| The (piezoelectrically stiffened) shear modulus (N·m) | |
| ξ | (m) |
| Density of the backing layer (kg·m) | |
| Density of the front load (kg·m) | |
| The density of the piezoelectric material (kg·m) | |
| Non-dimensionalised parameter given by Equation (13) | |
| Non-dimensionalised parameter given by Equation (14) | |
| The non-dimensionalised reception sensitivity given by Equation (10) | |
| The non-dimensionalised transmission sensitivity given by Equation (9) |
References
- Alfirevic, Z.; Stampalija, T.; Medley, N. Fetal and umbilical Doppler ultrasound in normal pregnancy. Cochrane Database Syst. Rev. 2015, 4, CD001450. [Google Scholar] [PubMed]
- Bricker, L.; Medley, N.; Pratt, J.J. Routine ultrasound in late pregnancy (after 24 weeks’ gestation). Cochrane Database Syst. Rev. 2015, 6, CD001451. [Google Scholar] [PubMed]
- Constantine, S.; Wilkinson, C. Double trouble: The importance of reporting chorionicity and amnionicity in twin pregnancy ultrasound reports. J. Med. Imag. Radiat. Oncol. 2015, 59, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.; Gallos, I.; Dobson, S.; Campbell, B.; Coomarasamy, A.; Raine-Fenning, N. Accuracy of first trimester ultrasound features for diagnosis of tubal ectopic pregnancy in the absence of an obvious extra-uterine embryo: A systematic review and meta-analysis. Ultrasound Obstet. Gynecol. 2015, 47, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Siafarikas, F.; Stær-Jensen, J.; Hilde, G.; Bø, K.; Ellström Engh, M. The levator ani muscle during pregnancy and major levator ani muscle defects diagnosed postpartum: A three-and four-dimensional transperineal ultrasound study. BJOG Int. J. Obstet. Gynaecol. 2015, 122, 1083–1091. [Google Scholar] [CrossRef] [PubMed]
- Cheong, Y.M.; Lee, D.H.; Jung, H.K. Ultrasonic guided wave parameters for detection of axial cracks in feeder pipes of PHWR nuclear power plants. Ultrasonics 2004, 42, 883–888. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.; Ditri, J.J.; Pilarski, A.; Rajana, K.; Carr, F. A guided wave inspection technique for nuclear steam generator tubing. NDT E Int. 1994, 27, 307–310. [Google Scholar] [CrossRef]
- Yang, J.; Lee, H.; Lim, H.J.; Kim, N.; Yeo, H.; Sohn, H. Development of a fiber-guided laser ultrasonic system resilient to high temperature and gamma radiation for nuclear power plant pipe monitoring. Meas. Sci. Technol. 2013, 24, 085003. [Google Scholar] [CrossRef]
- Hayward, G.; MacLeod, C.; Durrani, T. A systems model of the thickness mode piezoelectric transducer. J. Acoust. Soc. Am. 1984, 76, 369–382. [Google Scholar] [CrossRef]
- Hayward, G. A systems feedback representation of piezoelectric transducer operational impedance. Ultrasonics 1984, 22, 153–162. [Google Scholar] [CrossRef]
- Miles, R.; Hoy, R. The development of a biologically-inspired directional microphone for hearing aids. Audiol. Neurotol. 2006, 11, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Müller, R. A numerical study of the role of the tragus in the big brown bat. J. Acoust. Soc. Am. 2004, 116, 3701–3712. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.; Lu, H.; Zhang, S.; Peremans, H. A helical biosonar scanning pattern in the Chinese Noctule, Nyctalus plancyi. J. Acoust. Soc. Am. 2006, 119, 4083–4092. [Google Scholar] [CrossRef] [PubMed]
- Robert, D.; Göpfert, M.C. Novel schemes for hearing and orientation in insects. Curr. Opin. Neurobiol. 2002, 12, 715–720. [Google Scholar] [CrossRef]
- Orr, L.A.; Mulholland, A.J.; O’Leary, R.L.; Parr, A.; Pethrick, R.A.; Hayward, G. Theoretical modelling of frequency dependent elastic loss in composite piezoelectric transducers. Ultrasonics 2007, 47, 130–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mulholland, A.; Walker, A. Piezoelectric ultrasonic transducers with fractal geometry. Fractals 2011, 19, 469–479. [Google Scholar] [CrossRef]
- Eberl, D.F.; Hardy, R.W.; Kernan, M.J. Genetically similar transduction mechanisms for touch and hearing in Drosophila. J. Neurosci. 2000, 20, 5981–5988. [Google Scholar] [PubMed]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley and Sons: Chichester, UK, 2004. [Google Scholar]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001; Volume 143. [Google Scholar]
- Falconer, K.J.; Hu, J. Nonlinear diffusion equations on unbounded fractal domains. J. Math. Anal. Appl. 2001, 256, 606–624. [Google Scholar] [CrossRef]
- Schwalm, W.A.; Schwalm, M.K. Extension theory for lattice Green functions. Phys. Rev. B 1988, 37, 9524. [Google Scholar] [CrossRef]
- Mulholland, A.J. Bounds on the Hausdorff dimension of a renormalisation map arising from an excitable reaction-diffusion system on a fractal lattice. Chaos Solitons Fractals 2008, 35, 274–284. [Google Scholar] [CrossRef] [Green Version]
- Algehyne, E.A.; Mulholland, A.J. A finite element approach to modelling fractal ultrasonic transducers. IMA J. Appl. Math. 2015, 80, 1684–1702. [Google Scholar] [CrossRef]
- Yang, J. The Mechanics of Piezoelectric Structures; World Scientific: Singapore, Singapore, 2006; Volume 170. [Google Scholar]
- Giona, M. Transport phenomena in fractal and heterogeneous media input/output renormalization and exact results. Chaos Solitons Fractals 1996, 7, 1371–1396. [Google Scholar] [CrossRef]
- Giona, M.; Schwalm, W.A.; Schwalm, M.K.; Adrover, A. Exact solution of linear transport equations in fractal media I. Renormalization analysis and general theory. Chem. Eng. Sci. 1996, 51, 4717–4729. [Google Scholar] [CrossRef]
- Abdulbake, J.; Mulholland, A.J.; Gomatam, J. A renormalization approach to reaction-diffusion processes on fractals. Fractals 2003, 11, 315–330. [Google Scholar] [CrossRef]
- Abdulbake, J.; Mulholland, A.J.; Gomatam, J. Existence and stability of reaction diffusion waves on a fractal lattice. Chaos Solitons Fractals 2004, 20, 799–814. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley and Sons: New York, NY, USA, 1973; Volume 1. [Google Scholar]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar]




















| Parameter description | Symbol | Magnitude | Dimensions |
|---|---|---|---|
| Element of the stiffness tensor | N·m | ||
| Element of the piezoelectric tensor | 17 | C·m | |
| Element of the permittivity tensor | C (V·m) | ||
| Density of the piezoelectric material | 7500 | kg·m | |
| Parallel electrical impedance load | 1000 | Ω | |
| Series electrical impedance load | 50 | Ω | |
| Length of transducer | L | 1 | mm |
| Ratio of cross-sectional area to edge length | ξ | 0.4 | m |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barlow, E.; Algehyne, E.A.; Mulholland, A.J. Investigating the Performance of a Fractal Ultrasonic Transducer Under Varying System Conditions. Symmetry 2016, 8, 43. https://doi.org/10.3390/sym8060043
Barlow E, Algehyne EA, Mulholland AJ. Investigating the Performance of a Fractal Ultrasonic Transducer Under Varying System Conditions. Symmetry. 2016; 8(6):43. https://doi.org/10.3390/sym8060043
Chicago/Turabian StyleBarlow, Euan, Ebrahem A. Algehyne, and Anthony J. Mulholland. 2016. "Investigating the Performance of a Fractal Ultrasonic Transducer Under Varying System Conditions" Symmetry 8, no. 6: 43. https://doi.org/10.3390/sym8060043