Prototiles and Tilings from Voronoi and Delone Cells of the Root Lattice An
Abstract
:1. Introduction
2. The Root Lattice and Its Coxeter–Weyl Group
3. Projections of the Faces of the Voronoi and Delone Cells
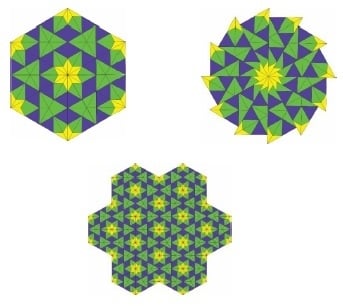
4. Examples of Prototiles and Patches of Tilings
4.1. Projection of the Voronoi Cell of
4.2. Projection of the Delone Cells of the Root Lattice
4.3. Projection of the Voronoi Cell of the Root Lattice
4.4. Projection of the Root Lattice by Delone Cells
4.5. Projection of the Voronoi Cell of the Root Lattice
4.6. Projection of the Delone Cells of the Root Lattice
4.7. Prototiles from the Projection of the Voronoi Cell of the Root Lattice
4.8. Projection of the Delone Cells of the Root Lattice
4.9. Prototiles from the Projection of the Voronoi CELL of the Root Lattice
4.10. Projection of the Delone Cells of the Root Lattice
4.11. Prototiles from Projection of the Voronoi Cell of the Root Lattice
4.12. Prototiles from the Projection of the Delone Cells of the Root Lattice
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Three-Dimensional Cube and the Voronoi Cell of
Appendix A.2. Five-Dimensional Cube and the Voronoi Cell of
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Di Vincenzo, D.; Steinhardt, P.J. Quasicrystals: The State of the Art; World Scientific Publishers: Singapore, 1991. [Google Scholar]
- Janot, C. Quasicrystals: A Primer, 2rd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Senechal, M. Quasicrystals and Geometry; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Baake, M.; Grimm, U. Aperiodic Order, Volume 1: A Mathematical Invitation; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; Freeman: New York, NY, USA, 1987. [Google Scholar]
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 1974, 10, 266–271. [Google Scholar]
- Penrose, R. Roger Penrose’s Pentaplexity article on aperiodic tiling. Eureka 1978, 39, 16–22. [Google Scholar]
- de Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. Nederl. Akad. Wetensch. Proc. Ser. 1981, 84, 38–66. [Google Scholar] [CrossRef]
- Duneau, M.; Katz, A. Quasiperiodic patterns. Phys. Rev. Lett. 1985, 54, 2688–2691. [Google Scholar] [CrossRef] [PubMed]
- Baake, M.; Joseph, D.; Kramer, P.; Schlottmann, M. Root lattices and quasicrystals. J. Phys. A Math. Gen. 1990, 23, L1037–L1041. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Moody, R.V.; Patera, J. Fields Institute for Research in Mathematical Sciences Monographs Series 10; AMS: Providence, RI, USA, 1998; pp. 135–178. [Google Scholar]
- Whittaker, E.J.W.; Whittaker, R.M. Some generalized Penrose patterns from projections of n-dimensional lattices. Acta Crystallogr. Sect. A Found. Adv. 1988, 44, 105–112. [Google Scholar]
- Koca, M.; Koca, N.; Koc, R. Group-theoretical analysis of aperiodic tilings from projections of higher-dimensional lattices Bn. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 175–185. [Google Scholar]
- Boyle, L.; Steinhardt, P.J. Coxeter pairs, Ammann patterns and Penrose-like tilings. arXiv 2016, arXiv:1608.08215. [Google Scholar]
- Koca, N.O.; Koca, M.; Al-Siyabi, A. SU (5) grand unified theory, its polytopes and 5-fold symmetric aperiodic tiling. Int. J. Geom. Methods Mod. Phys. 2018, 5, 1850058. [Google Scholar] [CrossRef]
- Masáková, Z.; Patera, J.; Pelantová, E. Inflation centres of the cut and project quasicrystals. J. Phys. A Math. Gen. 1998, 31, 1443. [Google Scholar] [CrossRef]
- Meyer, Y. Algebraic Numbers and Harmonic Analysis, 1st ed.; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Lagarias, J.C. Meyer’s concept of quasicrystal and quasiregular sets. Commun. Math. Phys. 1996, 179, 365–376. [Google Scholar] [CrossRef]
- Moody, R.V. Meyer Sets and Their Duals, in The Mathematics of Long-Range Aperiodic Order, NATO ASI Series C; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; Volume 489, pp. 403–441. [Google Scholar]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Für Die Reine Und Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Voronoi, G. Part II of Voronoi (1908). J. Für Die Reine Und Angew. Math. 1909, 136, 67–181. [Google Scholar] [CrossRef]
- Delaunay, N.B. Izv. Sur la partition régulière de l’espace à 4 dimensions. Première partie. Akad. Nauk SSSR Otdel. Fiz. Mat. Nauk. 1929, 1, 79–110. [Google Scholar]
- Delaunay, N.B. Geometry of positive quadratic forms. Usp. Mat. Nauk. 1938, 3, 16–62. [Google Scholar]
- Delaunay, N.B. Geometry of positive quadratic forms. Part II. Usp. Mat. Nauk. 1938, 4, 102–164. [Google Scholar]
- Conway, J.H.; Sloane, N.J.A. Sphere Packings, Lattices and Groups; Springer: New York, NY, USA, 1988. [Google Scholar]
- Conway, J.H.; Sloane, N.J.A. Miscellanea Mathematica; Hilton, P., Hirzebruch, F., Remmert, R., Eds.; Springer: New York, NY, USA, 1991; pp. 71–108. [Google Scholar]
- Deza, M.; Grishukhin, V. Nonrigidity degrees of root lattices and their duals. Geom. Dedicate 2004, 104, 15–24. [Google Scholar] [CrossRef]
- Engel, P. Geometric Crystallography: An Axiomatic Introduction to Crystallography; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Engel, P.; Michel, L.; Senechal, M. Lattice geometry. Preprint IHES /P/04/45. 1994. [Google Scholar]
- Moody, R.V.; Patera, J. Voronoi and Delaunay cells of root lattices: Classification of their faces and facets by Coxeter-Dynkin diagrams. J. Phys. A Math. Gen. 1992, 25, 5089–5134. [Google Scholar] [CrossRef]
- Koca, M.; Ozdes Koca, N.; Al-Siyabi, A.; Koc, R. Explicit construction of the Voronoi and Delaunay cells of W(An) and W(Dn) lattices and their facets. Acta Crystallogr. Sect. A Found. Adv. 2018, 74, 499–511. [Google Scholar]
- Ausloos, M.; Bartolacci, F.; Castellano, N.G.; Cerqueti, R. Exploring how innovation strategies at time of crisis influence performance: A cluster analysis perspective. Technol. Anal. Strateg. Manag. 2018, 30, 484–497. [Google Scholar] [CrossRef]
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications: New York, NY, USA, 1973. [Google Scholar]
- Grünbaum, B. Convex Polytopes; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Humphreys, J.E. Cambridge Studies in Advanced Mathematics, Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1990; Volume 29. [Google Scholar]
- Michel, L. Bravais Classes, Voronoi Cells, Delone Cells, Symmetry and Structural Properties of Condensed Matter; Lulek, T., Florek, W., Walcerz, S., Eds.; World Scientific: Singapore, 1995; p. 279. [Google Scholar]
- Michel, L. Complete Description of the Voronoi Cell of the Lie Algebra An Weight Lattice. On the Bounds for the Number of d-Faces of the n-Dimensional Voronoi Cells, Algebraic Methods in Physics; Saint-Aubin, Y., Vinet, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 149–171. [Google Scholar]
- Koca, M.; Koca, N.O.; Koc, R. Affine Coxeter group Wa (A4), quaternions, and decagonal quasicrystals. Int. J. Geom. Meth. Mod. Phys. 2014, 11, 1450031. [Google Scholar] [CrossRef]
- Carter, R.W. Simple Groups of Lie Type; John Wiley & Sons: New York, NY, USA, 1972; pp. 158–169. [Google Scholar]
- Nischke, K.P.; Danzer, L. A construction of inflation rules based on n-fold symmetry. Discret. Comput. Geom. 1996, 15, 221–236. [Google Scholar] [CrossRef]


















| Root Lattice | h | # of Prototiles | Rhombuses with Pairs of Angles |
|---|---|---|---|
| 4 | 1 | , (square) | |
| 5 | 2 | , (Penrose’s thick and thin rhombuses) | |
| 6 | 1 | ||
| 7 | 3 | ||
| 8 | 2 | , (Amman-Beenker tiles) | |
| 9 | 4 | ||
| 10 | 2 | (Penrose’ thick and thin rhombuses) | |
| 11 | 3 | ||
| 12 | 3 |
| Root Lattice | h | # of Prototiles | Triangles Denoted by Triple Natural Numbers |
|---|---|---|---|
| 3 | 1 | ||
| 4 | 1 | (right triangle) | |
| 5 | 2 | (Robinson triangles) | |
| 6 | 3 | ||
| 7 | 4 | (Danzer triangles) | |
| 8 | 5 | ||
| 9 | 7 | ||
| 10 | 8 | ||
| 11 | 10 | ||
| 12 | 12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozdes Koca, N.; Al-Siyabi, A.; Koca, M.; Koc, R. Prototiles and Tilings from Voronoi and Delone Cells of the Root Lattice An. Symmetry 2019, 11, 1082. https://doi.org/10.3390/sym11091082
Ozdes Koca N, Al-Siyabi A, Koca M, Koc R. Prototiles and Tilings from Voronoi and Delone Cells of the Root Lattice An. Symmetry. 2019; 11(9):1082. https://doi.org/10.3390/sym11091082
Chicago/Turabian StyleOzdes Koca, Nazife, Abeer Al-Siyabi, Mehmet Koca, and Ramazan Koc. 2019. "Prototiles and Tilings from Voronoi and Delone Cells of the Root Lattice An" Symmetry 11, no. 9: 1082. https://doi.org/10.3390/sym11091082