Calibration of the Surface Renewal Method (SR) under Different Meteorological Conditions in an Avocado Orchard
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
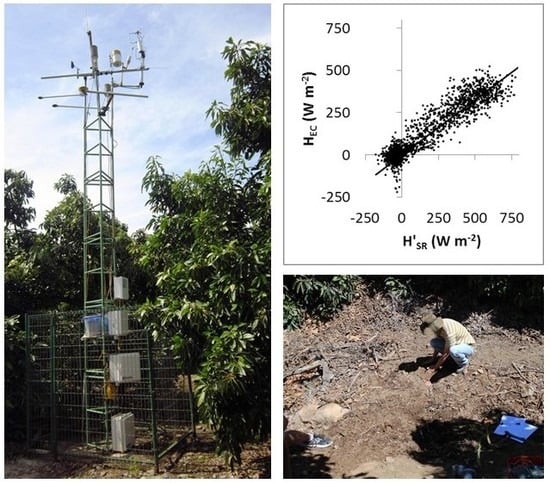
2.2. Measurement of Energy Balance Components
2.2.1. Turbulent Fluxes Measurements (H and LE)
2.2.2. Measurements of Net Radiation (Rn) and Soil Heat Flux (G)
2.3. Evaluation of the Energy Balance Closure (EBC)
2.4. Surface Renewal Method (SR)
2.5. Meteorological Categories
2.5.1. Categorization by Wind Condition
2.5.2. Categorization by Solar Radiation (Sunny and Cloudy Days)
2.6. Calibration Factor Alpha (α)
2.7. Statistical Analysis
3. Results and Discussion
3.1. Meteorological Categories
3.2. The Effect of the Alpha Value in the Estimation of the Sensible Heat Flux
3.3. Estimation of HSR With a Fixed Alpha Value
3.4. Estimation of HSR with Variable Alpha Values
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Holzapfel, E.; De Souza, J.A.; Jara, J.; Carvallo, H. Responses of avocado production to variation in irrigation levels. Irrig. Sci. 2017, 35, 205–215. [Google Scholar] [CrossRef]
- Lahav, E.; Kalmar, D. Determination of the Irrigation Regimen for an Avocado Plantation in Spring and Autumn. Aust. J. Agric. Res. 1983, 34, 717–724. [Google Scholar] [CrossRef] [Green Version]
- Lahav, E.; Whiley, A.W.; Turner, D.W. Irrigation and Mineral Nutrition. In The Avocado Botany, Production and Uses, 2nd ed.; Schaffer, B., Wolstenholme, B.N., Whiley, A.W., Eds.; CAB International: Croydon, UK, 2013; pp. 301–341. ISBN 978 1 84593 701 0. [Google Scholar]
- Neuhaus, A.; Turner, D.W.; Colmer, T.D.; Kuo, J.; Eastham, J. Drying half the root-zone of potted avocado (Persea americana Mill., cv. Hass) trees avoids the symptoms of water deficit that occur under complete root-zone drying. J. Hortic. Sci. Biotechnol. 2007, 82, 679–689. [Google Scholar] [CrossRef]
- Ferreyra, R.; Sellés, G.; Burgos, L.; Villagra, P.; Sepúlveda, P.; Lemus, G. Manejo Riego en Frutales en Condiciones de Restricción Hídrica, Boletín INIA nº 214; Instituto Nacional de Investigaciones Agropecuarias: Santiago, Chile, 2010; pp. 65–72. ISSN 0717-4829. [Google Scholar]
- FAO. Evapotranspiración del Cultivo. Guías para la Determinación de Los Requerimientos de Agua de Los Cultivos; Food and Agriculture Organization: Roma, Italy, 2006; pp. 1–79. ISBN 92-5-304219-2. [Google Scholar]
- Katerji, N.; Rana, G. FAO-56 methodology for determining water requirement of irrigated crops: Critical examination of the concepts, alternative proposals and validation in Mediterranean region. Theor. Appl. Climatol. 2013, 116, 515–536. [Google Scholar] [CrossRef]
- Zapata, N.; Martínez-Cob, A. Estimation of sensible and latent heat flux from natural sparse vegetation surfaces using surface renewal. J. Hydrol. 2001, 254, 215–228. [Google Scholar] [CrossRef] [Green Version]
- Zapata, N.; Martínez-Cob, A. Evaluation of the surface renewal method to estimate wheat evapotranspiration. Agric. Water Manag. 2002, 55, 141–157. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Buttar, N.A.; Tanny, J.; Snyder, R.L.; Savage, M.J.; Lakhiar, I.A. Surface Renewal Application for Estimating Evapotranspiration: A Review. Adv. Meteorol. 2018, 2018, 1–11. [Google Scholar] [CrossRef] [Green Version]
- López-Olivari, R.; Ortega-Farías, S.; Poblete-Echeverría, C. Energy balance components and evapotranspiration measurements over a superintensive olive orchard. Int. Symp. Irrig. Hortic. Crops 2007, 1150. [Google Scholar] [CrossRef]
- Qiu, J.; Su, H.B.; Watanabe, T.; Brunet, Y. Surface renewal analysis: A new method to obtain scalar fluxes. Agric. For. Meteorol. 1995, 74, 119–137. [Google Scholar] [CrossRef]
- Spano, D.; Snyder, R.L.; Duce, P. Surface renewal analysis for sensible heat flux density using structure functions. Agric. For. Meteorol. 1997, 86, 259–271. [Google Scholar] [CrossRef]
- Snyder, R.L.; Spano, D.; Pawu, K.T. Surface renewal analysis for sensible heat and latent heat flux density. Bound. -Layer Meteorol. 1996, 77, 249–266. [Google Scholar] [CrossRef]
- Spano, D.; Duce, P.; Snyder, R.L.; Paw, U.K.T. Surface renewal estimates of evapotranspiration. Tall canopies. Int. Symp. Irrig. Hortic. Crops 1997, 449, 63–68. [Google Scholar] [CrossRef]
- Chen, W.; Novak, M.D.; Black, T.A.; Lee, X. Coherent eddies and temperature structure functions for three contrasting surfaces. Part II: Renewal model for sensible heat flux. Bound. -Layer Meteorol. 1997, 84, 125–147. [Google Scholar] [CrossRef]
- Duce, P.; Spano, D.; Snyder, R.L.; Paw, U.K.T. Surface renewal estimates of evapotranspiration. Short canopies. Int. Symp. Irrig. Hortic. Crops 1997, 449, 57–62. [Google Scholar] [CrossRef]
- Spano, D.; Snyder, R.L.; Duce, P. Estimating sensible and latent heat flux densities from grapevine canopies using surface renewal. Agric. For. Meteorol. 2000, 104, 171–183. [Google Scholar] [CrossRef]
- Castellví, F. Combining surface renewal analysis and similarity theory: A new approach for estimating sensible heat flux. Water Resour. Res. 2004, 40, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Poblete-Echeverria, C.; Ortega-Farias, S. Estimation of vineyard evapotranspiration using the surface renewal and residual energy balance methods. Int. Symp. Irrig. Hortic. Crops 2014, 1038, 633–638. [Google Scholar] [CrossRef]
- Santibáñez, F.; Uribe, J. Atlas Agroclimático de Chile, Regiones V y Metropolitana; Universidad de Chile: Santiago, Chile, 1990; pp. 3–65. [Google Scholar]
- CIREN. Descripciones de Suelo, Materiales y Símbolos. Estudio Agrológico V Región, Tomo 2; Publicación 116; Centro de Información de Recursos Naturales: Santiago, Chile, 1997. [Google Scholar]
- Lemus, G.; Ferreyra, R.; Gil, P.; Maldonado, P.; Toledo, C.; Barrera, C.; de Celedón, A.J.M. El Cultivo del Palto, Boletín INIA nº 129; Instituto de Investigaciones Agropecuarias: La Cruz, Chile, 2005; pp. 53–64. ISSN 0717-4829. [Google Scholar]
- Kormann, R.; Meixner, F. An analytical footprint model for non-neutral stratification. Bound. -Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Hsieh, C.; Katul, G.; Chi, T. An approximate analytical model for footprint estimation of scaler fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Shapland, T.M.; Snyder, R.L.; Smart, D.R.; Williams, L.E. Estimation of actual evapotranspiration in winegrape vineyards located on hillside terrain using surface renewal analysis. Irrig. Sci. 2012, 30, 471–484. [Google Scholar] [CrossRef]
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural, and Regulatory Applications; LI-COR® Biosciences: Lincoln, NE, USA, 2013; pp. 7–30. ISBN 978-0-615-76827-4. [Google Scholar]
- Balbontín–Nesvara, C.; Calera-Belmonte, A.; González-Piqueras, J.; Campos–Rodríguez, I.; Llanos López-González, M.; Torres-Prieto, E. Comparación de los sistemas covarianza y relación de Bowen en la evapotranspiración de un viñedo bajo clima semi–árido. Agrociencia 2011, 45, 87–103. [Google Scholar]
- Abraha, M.G. Sensible Heat Flux and Evaporation for Sparse Vegetation Using Temperature-Variance and a Dual-Source Model. Ph.D. Thesis, University of KwaZulu-Natal, Pietermaritzburg, South Africa, 2010. [Google Scholar]
- Van Atta, C.W. Effect of coherent structures on structure functions of temperature in the atmospheric boundary layer. Arch. Mech. Stosow. 1977, 29, 161–171. [Google Scholar]
- Gao, W.; Shaw, R.H. Observation of organized structure in turbulent flow within and above a forest canopy. Bound. -Layer Meteorol. 1989, 47, 349–377. [Google Scholar] [CrossRef]
- Snyder, R.L.; Paw, U.K.T.; Spano, D.; Duce, P. Surface renewal estimates of evapotranspiration. Theory. Int. Symp. Irrig. Hortic. Crops 1997, 449, 49–55. [Google Scholar] [CrossRef]
- McElrone, A.J.; Shapland, T.M.; Calderon, A.; Fitzmaurice, L.; Snyder, R.L. Surface Renewal: An Advanced Micrometeorological Method for Measuring and Processing Field-Scale Energy Flux Density Data. JoVE (J. Vis. Exp.) 2013, 82, e50666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xenakis, G. FREddyPro: Post-Processing EddyPro Full Output File. r package version 1.0. 2016. Available online: https://CRAN.Rproject.org/package=FREddyPro (accessed on 1 April 2020).
- Castellví, F.; Snyder, R.L. Sensible heat flux estimates using surface renewal analysis. A study case over a peach orchard. Agric. For. Meteorol. 2009, 149, 1397–1402. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef] [Green Version]
- Poblete-Echeverria, C.; Ortega-Farias, S. Estimation of actual evapotranspiration for a drip-irrigated Merlot vineyard using a three-source model. Irrig. Sci. 2009, 28, 65–78. [Google Scholar] [CrossRef]
- Essa, K.S.M.; Embaby, M.M.; Kozae, A.M.; Mubarak, F.; Kamel, I. Estimation of Seasonal Atmospheric Stability and Mixing Height by Using Different Schemes. In Proceedings of the VIII Radiation Physics & Protection Conference, Fayoum, Egypt, 13–15 November 2006. [Google Scholar]
- Cullen, S. Trees and wind: Wind scales and speeds. J. Arboric. 2005, 28, 237–242. [Google Scholar]
- RMETS. Available online: https://www.rmets.org/weather-and-climate/observing/beaufort-scale (accessed on 28 February 2018).
- NOAA. Available online: http://www.spc.noaa.gov/faq/tornado/beaufort.html (accessed on 28 February 2018).
- NWS. Available online: http://w1.weather.gov/glossary/index.php?letter=b (accessed on 28 February 2018).
- AGROMET. Available online: http://agromet.inia.cl/ (accessed on 21 December 2017).
- Rivero, M.; Orozco, S.; Sellschopp, F.S.; Loera-Palomo, R. A new methodology to extend the validity of the Hargreaves-Samani model to estimate global solar radiation in different climates: Case study Mexico. Renew. Energy 2017, 114, 1340–1352. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, NY, USA, 2009; p. 213. ISBN 978-0-387-98141-3. [Google Scholar]
- Willmott, C.J. On the validation models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Mayer, D.G.; Butler, D.G. Statistical validation. Ecol. Model. 1993, 68, 21–32. [Google Scholar] [CrossRef]
- Snyder, R.L.; O’Connell, N.V. Crop coefficients for microsprinkler-irrigated clean-cultivated, mature citrus in an arid climate. J. Irrig. Drain. Eng. 2007, 133, 1. [Google Scholar] [CrossRef]
- Castellví, F.; Consoli, S.; Papa, R. Sensible heat flux estimates using two different methods based on surface renewal analysis. A study case over an orange orchard in Sicily. Agric. For. Meteorol. 2012, 152, 58–64. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Sepúlveda-Reyes, D.; Ortega-Farías, S. Effect of height and time lag on the estimation of sensible heat flux over a drip-irrigated vineyard using the surface renewal (SR) method across distinct phenological stages. Agric. Water Manag. 2014, 141, 74–83. [Google Scholar] [CrossRef]



| KT Ranges | Category | n (Days) |
|---|---|---|
| 0.6 < KT ≤ 1.0 | Sunny | 47 |
| 0.0 < KT ≤ 0.6 | Cloudy | 18 |
| (a) 30-min α = 0.66, r2 = 0.92 | (b) Daily α = 0.66, r2 = 0.92 | (c) Daily α = 0.73, r2 = 0.98 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Dataset | n (h.h) | RMSE (A.C) | MAE (A.C) | n (Days) | RMSE (A.C) | MAE (A.C) | n (Days) | RMSE (A.C) | MAE (A.C) |
| WD | 3120 | 52.25 | 36.33 | 65 | 1.50 | 1.29 | 65 | 1.22 | 0.95 |
| S | 2256 | 54.66 | 39.53 | 47 | 1.49 | 1.28 | 47 | 1.25 | 0.95 |
| C | 864 | 45.36 | 27.96 | 18 | 1.54 | 1.34 | 18 | 1.14 | 0.97 |
| LW | 1344 | 49.69 | 32.31 | 28 | 1.63 | 1.41 | 28 | 1.29 | 1.02 |
| MW | 1776 | 54.11 | 39.37 | 37 | 1.40 | 1.20 | 37 | 1.17 | 0.91 |
| S-LW | 624 | 56.00 | 39.12 | 13 | 1.96 | 1.75 | 13 | 1.59 | 1.26 |
| S-MW | 1632 | 54.14 | 39.69 | 34 | 1.26 | 1.09 | 34 | 1.09 | 0.83 |
| C-LW | 720 | 43.49 | 26.40 | 15 | 1.27 | 1.12 | 15 | 0.96 | 0.80 |
| C-MW | 144 | 53.75 | 35.72 | 3 | 2.47 | 2.46 | 3 | 1.79 | 1.78 |
| (a) 30-min | (b) Daily | (c) Daily | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | n (h.h) | α | r2 | RMSE (A.C) | MAE (A.C) | n (Days) | α | RMSE (A.C) | MAE (A.C) | n (Days) | α | r2 | RMSE (A.C) | MAE (A.C) |
| WD | 3120 | 0.66 | 0.92 | 52.25 | 36.33 | 65 | 0.66 | 1.50 | 1.29 | 65 | 0.73 | 0.98 | 1.22 | 0.95 |
| S | 2256 | 0.65 | 0.92 | 54.47 | 39.31 | 47 | 0.65 | 1.62 | 1.42 | 47 | 0.72 | 0.99 | 1.25 | 0.97 |
| C | 864 | 0.76 | 0.92 | 41.52 | 26.71 | 18 | 0.76 | 1.03 | 0.84 | 18 | 0.79 | 0.98 | 0.99 | 0.79 |
| LW | 1344 | 0.69 | 0.92 | 49.32 | 32.12 | 28 | 0.69 | 1.46 | 1.23 | 28 | 0.75 | 0.98 | 1.26 | 0.94 |
| MW | 1776 | 0.65 | 0.92 | 53.98 | 39.19 | 37 | 0.65 | 1.51 | 1.32 | 37 | 0.72 | 0.99 | 1.16 | 0.92 |
| S-LW | 624 | 0.67 | 0.92 | 56.00 | 39.12 | 13 | 0.67 | 1.95 | 1.74 | 13 | 0.75 | 0.98 | 1.57 | 1.20 |
| S-MW | 1632 | 0.64 | 0.93 | 53.77 | 39.29 | 34 | 0.64 | 1.45 | 1.29 | 34 | 0.71 | 0.99 | 1.06 | 0.85 |
| C-LW | 720 | 0.74 | 0.92 | 41.18 | 26.03 | 15 | 0.74 | 0.93 | 0.77 | 15 | 0.77 | 0.98 | 0.91 | 0.70 |
| C-MW | 144 | 0.84 | 0.95 | 38.86 | 24.96 | 3 | 0.84 | 0.80 | 0.68 | 3 | 0.90 | 0.99 | 0.56 | 0.48 |
| Dataset | WD | S | C | LW | MW | S-LW | S-MW | C-LW | C-MW |
|---|---|---|---|---|---|---|---|---|---|
| WD | - | False | False | False | False | True | False | False | False |
| S | 0.003 | - | False | False | True | True | True | False | False |
| C | <0.001 | <0.001 | - | False | False | False | False | True | False |
| LW | <0.001 | <0.001 | <0.001 | - | False | False | False | False | False |
| MW | 0.021 | 0.680 | <0.001 | <0.001 | - | True | True | False | False |
| S-LW | 0.868 | 0.055 | <0.001 | 0.013 | 0.110 | - | False | False | False |
| S-MW | <0.001 | 0.311 | <0.001 | <0.001 | 0.179 | 0.011 | - | False | False |
| C-LW | <0.001 | <0.001 | 0.064 | <0.001 | <0.001 | <0.001 | <0.001 | - | False |
| C-MW | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morán, A.; Ferreyra, R.; Sellés, G.; Salgado, E.; Cáceres-Mella, A.; Poblete-Echeverría, C. Calibration of the Surface Renewal Method (SR) under Different Meteorological Conditions in an Avocado Orchard. Agronomy 2020, 10, 730. https://doi.org/10.3390/agronomy10050730
Morán A, Ferreyra R, Sellés G, Salgado E, Cáceres-Mella A, Poblete-Echeverría C. Calibration of the Surface Renewal Method (SR) under Different Meteorological Conditions in an Avocado Orchard. Agronomy. 2020; 10(5):730. https://doi.org/10.3390/agronomy10050730
Chicago/Turabian StyleMorán, Andrés, Raúl Ferreyra, Gabriel Sellés, Eduardo Salgado, Alejandro Cáceres-Mella, and Carlos Poblete-Echeverría. 2020. "Calibration of the Surface Renewal Method (SR) under Different Meteorological Conditions in an Avocado Orchard" Agronomy 10, no. 5: 730. https://doi.org/10.3390/agronomy10050730