A Fast and Efficient Approach to Strength Prediction for Carbon/Epoxy Composites with Resin-Missing Defects
Abstract
:1. Introduction
2. Problem Statement
3. Construction of Prediction Models
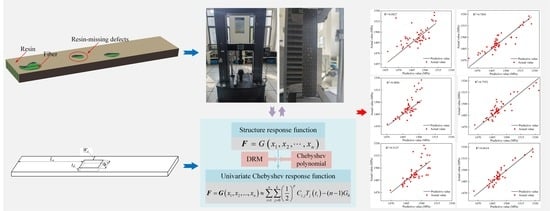
3.1. Chebyshev Polynomial Fitting
3.2. Dimension Reduction Method (DRM)
3.3. Univariate Chebyshev Prediction Model (UCPM)
3.4. Finite Element Analysis
4. Specimens and Experiments
4.1. Specimen Preparation
4.2. Experimental Method
5. Results and Discussion
5.1. Experimental Results
5.2. Finite Element Results
5.3. Accuracy Analysis of Strength Prediction Model
5.4. Performance Evaluation of UCPMs of Different Orders
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Tu, S.; Liu, Y.; Lu, X.; Zhu, X. Mechanical Properties of L-Joint with Composite Sandwich Structure. Compos. Struct. 2019, 217, 165–174. [Google Scholar] [CrossRef]
- Saberian, M.H.; Ashenai Ghasemi, F.; Ghasemi, I.; Bagheri, M.S. Morphology, Mechanical Behavior, and Prediction of A-Glass/SiO2/Epoxy Nanocomposite Using Response Surface Methodology. J. Elastomers Plast. 2019, 51, 669–683. [Google Scholar] [CrossRef]
- Ashenai Ghasemi, F.; Ghasemi, I.; Menbari, S.; Ayaz, M.; Ashori, A. Optimization of Mechanical Properties of Polypropylene/Talc/Graphene Composites Using Response Surface Methodology. Polym. Test. 2016, 53, 283–292. [Google Scholar] [CrossRef]
- Ghasemi, F.A.; Niyaraki, M.N.; Ghasemi, I.; Daneshpayeh, S. Predicting the Tensile Strength and Elongation at Break of PP/Graphene/Glass Fiber/EPDM Nanocomposites Using Response Surface Methodology. Mech. Adv. Mater. Struct. 2021, 28, 981–989. [Google Scholar] [CrossRef]
- Siddique, S.H.; Faisal, S.; Ali, M.; Gong, R.H. Optimization of Process Variables for Tensile Properties of Bagasse Fiber-Reinforced Composites Using Response Surface Methodology. Polym. Polym. Compos. 2021, 29, 1304–1312. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Zou, H.; Yu, M.; Xie, W. Optimizing Synthesis Parameters of Short Carbon Fiber Reinforced Polysulfonamide Composites by Using Response Surface Methodology. Polym. Test. 2017, 59, 355–361. [Google Scholar] [CrossRef]
- Srinivasan, R.; Pridhar, T.; Kirubakaran, R.; Ramesh, A. Prediction of Wear Strength of Squeeze Cast Aluminium Hybrid Metal Matrix Composites Using Response Surface Methodology. Mater. Today Proc. 2020, 27, 1806–1811. [Google Scholar] [CrossRef]
- Liu, J.; He, B.; Yan, T.; Yu, F.; Shen, Y. Study on Carbon Fiber Composite Hull for AUV Based on Response Surface Model and Experiments. Ocean Eng. 2021, 239, 109850. [Google Scholar] [CrossRef]
- Haeri, A.; Fadaee, M.J. Efficient Reliability Analysis of Laminated Composites Using Advanced Kriging Surrogate Model. Compos. Struct. 2016, 149, 26–32. [Google Scholar] [CrossRef]
- Davidson, P.; Waas, A.M. Probabilistic Defect Analysis of Fiber Reinforced Composites Using Kriging and Support Vector Machine Based Surrogates. Compos. Struct. 2018, 195, 186–198. [Google Scholar] [CrossRef]
- Ameryan, A.; Ghalehnovi, M.; Rashki, M. Investigation of Shear Strength Correlations and Reliability Assessments of Sandwich Structures by Kriging Method. Compos. Struct. 2020, 253, 112782. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.-Y.; Wang, Y.; Feng, N.; Qu, M.-J.; Wu, L.-H. Mathematical Modeling for the Mechanical Properties of Poly(Vinylchloride) Ternary Composites. Polym. Eng. Sci. 2016, 56, 1109–1117. [Google Scholar] [CrossRef]
- Su, D.-X.; Zhao, J.; Wang, Y.; Qu, M.-J. Kriging-Based Orthotropic Closure for Flow-Induced Fiber Orientation and the Part Stiffness Predictions with Experimental Investigation. Polym. Compos. 2019, 40, 3844–3856. [Google Scholar] [CrossRef]
- Zhou, C.; Li, C.; Zhang, H.; Zhao, H.; Zhou, C. Reliability and Sensitivity Analysis of Composite Structures by an Adaptive Kriging Based Approach. Compos. Struct. 2021, 278, 114682. [Google Scholar] [CrossRef]
- Keshtegar, B.; Nguyen-Thoi, T.; Truong, T.T.; Zhu, S.-P. Optimization of Buckling Load for Laminated Composite Plates Using Adaptive Kriging-Improved PSO: A Novel Hybrid Intelligent Method. Def. Technol. 2021, 17, 85–99. [Google Scholar] [CrossRef]
- Suresh Kumar, C.; Arumugam, V.; Sengottuvelusamy, R.; Srinivasan, S.; Dhakal, H.N. Failure Strength Prediction of Glass/Epoxy Composite Laminates from Acoustic Emission Parameters Using Artificial Neural Network. Appl. Acoust. 2017, 115, 32–41. [Google Scholar] [CrossRef]
- Hammoudi, A.; Moussaceb, K.; Belebchouche, C.; Dahmoune, F. Comparison of Artificial Neural Network (ANN) and Response Surface Methodology (RSM) Prediction in Compressive Strength of Recycled Concrete Aggregates. Constr. Build. Mater. 2019, 209, 425–436. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Jiang, B.; Wang, R.; Liu, Y.; Jia, L. Mechanical Properties Prediction of Composite Laminate with FEA and Machine Learning Coupled Method. Compos. Struct. 2022, 299, 116086. [Google Scholar] [CrossRef]
- Liu, Y.; Lei, Z.; Zhu, R.; Shang, Y.; Bai, R. Artificial Neural Network Prediction of Residual Compressive Strength of Composite Stiffened Panels with Open Crack. Ocean Eng. 2022, 266, 112771. [Google Scholar] [CrossRef]
- Shanmugasundaram, N.; Praveenkumar, S.; Gayathiri, K.; Divya, S. Prediction on Compressive Strength of Engineered Cementitious Composites Using Machine Learning Approach. Constr. Build. Mater. 2022, 342, 127933. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M.L. Machine Learning Prediction of Compressive Strength for Phase Change Materials Integrated Cementitious Composites. Constr. Build. Mater. 2020, 265, 120286. [Google Scholar] [CrossRef]
- Lee, K.; Son, H.; Cho, K.; Choi, H. Effect of Interfacial Bridging Atoms on the Strength of Al/CNT Composites: Machine-Learning-Based Prediction and Experimental Validation. J. Mater. Res. Technol. 2022, 17, 1770–1776. [Google Scholar] [CrossRef]
- Zakaulla, M.; kesarmadu Siddalingappa, S. Prediction of Mechanical Properties for Polyetheretherketone Composite Reinforced with Graphene and Titanium Powder Using Artificial Neural Network. Mater. Today Proc. 2022, 49, 1268–1274. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Chen, L.; Luo, Z. A Chebyshev Interval Method for Nonlinear Dynamic Systems under Uncertainty. Appl. Math. Model. 2013, 37, 4578–4591. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of Mathematical Functions: With Formulas, Graphs and Mathematical Tables. Am. J. Phys. 1988, 56, 958. [Google Scholar] [CrossRef]
- Li, G.; Rosenthal, C.; Rabitz, H. High Dimensional Model Representations. J. Phys. Chem. A 2001, 105, 7765–7777. [Google Scholar] [CrossRef]
- Rabitz, H.; Aliş, Ö.F. General foundations of high-dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Rahman, S.; Xu, H. A Univariate Dimension-Reduction Method for Multi-Dimensional Integration in Stochastic Mechanics (Vol 19, Pg 393, 2004). Probab. Eng. Eng. Mech. 2006, 21, 97–98. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech.-Trans. ASME 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. Matthews A Progressive Damage Model for Mechanically Fastened Joints in Composite Laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2008. [CrossRef]











| Variables | Minimum/mm | Maximum/mm |
|---|---|---|
| Le | 0 | 115 |
| We | 2 | 12.5 |
| Wd | 4 | 25 |
| td | 0.225 | 1.35 |
| Elastic Modulus/GPa | Poisson’s Ratio | Shear Modulus/GPa | |||
|---|---|---|---|---|---|
| E11 | E22 = E33 | μ12 = μ13 | μ23 | G12 = G13 | G23 |
| 125 | 8.193 | 0.3 | 0.4 | 3.307 | 3.151 |
| Tensile Strength /MPa | Comprehensive Strength /MPa | Shear Strength /MPa | |||
| XT | YT = ZT | XC | YC = ZC | S12 = S13 | S23 |
| 1630 | 25 | 592 | 98 | 53 | 38 |
| Elastic Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | |||
|---|---|---|---|---|---|
| E11 | E22 = E33 | μ12 = μ13 | μ23 | XT | YT = ZT |
| 95.88 | 1 × 10−5 | 0.3 | 0.2 | 1367 | 1 × 10−5 |
| Resin-Missing Defect | 5.3% | 8.0% | 10.7% | 13.3% | 16.7% |
|---|---|---|---|---|---|
| Experimental (MPa) | 1570.46 | 1567.56 | 1509.19 | 1495.71 | 1384.72 |
| FEM (MPa) | 1563.34 | 1539.09 | 1522.7 | 1511.94 | 1427.11 |
| Error (%) | 0.45 | 1.82 | 0.90 | 1.09 | 3.06 |
| Defect— 5.3% | Defect— 8.0% | Defect— 10.7% | Defect— 13.3% | Defect— 16.7% | |
|---|---|---|---|---|---|
| Experimental/MPa | 1570.46 | 1567.56 | 1509.19 | 1495.71 | 1384.72 |
| Prediction/MPa | 1499.81 | 1490.27 | 1485.93 | 1474.36 | 1456.79 |
| Error/% | 4.50 | 4.93 | 1.54 | 1.43 | 5.20 |
| Order | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th |
|---|---|---|---|---|---|---|---|---|
| R2 | 0.0827 | 0.4886 | 0.5137 | 0.7493 | 0.7552 | 0.8614 | 0.7146 | 0.7313 |
| RMAE | 4.1931 | 3.3212 | 3.2529 | 1.3063 | 1.2222 | 0.7363 | 1.2374 | 1.1873 |
| RAAE | 0.0180 | 0.0130 | 0.0127 | 0.0103 | 0.0098 | 0.0076 | 0.0118 | 0.0107 |
| Sample points | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, F.; Zhu, L. A Fast and Efficient Approach to Strength Prediction for Carbon/Epoxy Composites with Resin-Missing Defects. Polymers 2024, 16, 742. https://doi.org/10.3390/polym16060742
Li H, Li F, Zhu L. A Fast and Efficient Approach to Strength Prediction for Carbon/Epoxy Composites with Resin-Missing Defects. Polymers. 2024; 16(6):742. https://doi.org/10.3390/polym16060742
Chicago/Turabian StyleLi, Hongfeng, Feng Li, and Lingxue Zhu. 2024. "A Fast and Efficient Approach to Strength Prediction for Carbon/Epoxy Composites with Resin-Missing Defects" Polymers 16, no. 6: 742. https://doi.org/10.3390/polym16060742