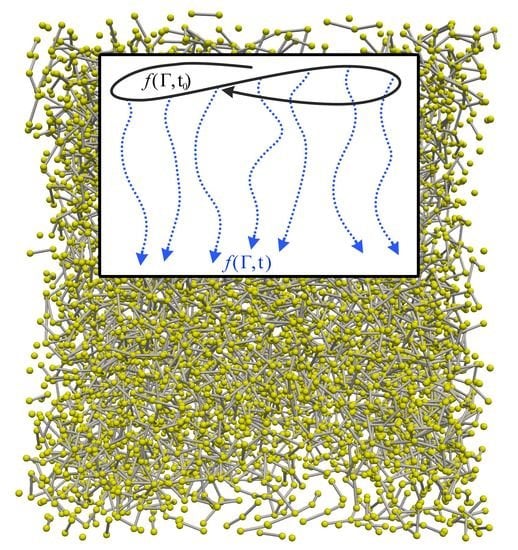
Simulating Polymerization by Boltzmann Inversion Force Field Approach and Dynamical Nonequilibrium Reactive Molecular Dynamics
Abstract
:1. Introduction
- (1)
- Initiation:
- (2)
- Propagation:
- (3)
- Termination:
2. Models and Methods
2.1. Coarse-Grained Potential
2.2. Coarse-Grained Reaction Modeling
2.3. Dynamical Approach to Nonequilibrium Molecular Dynamics
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.Y.; Windall, G.; Boyd, I.W. UV curing of optical fibre coatings using excimer lamps. Appl. Surf. Sci. 2002, 186, 568–572. [Google Scholar] [CrossRef]
- Rosero-Navarro, N.; Pellice, S.; Castro, Y.; Aparicio, M.; Durán, A. Improved corrosion resistance of AA2024 alloys through hybrid organic–inorganic sol–gel coatings produced from sols with controlled polymerisation. Surf. Coat. Technol. 2009, 203, 1897–1903. [Google Scholar] [CrossRef]
- Layani, M.; Wang, X.; Magdassi, S. Novel Materials for 3D Printing by Photopolymerization. Adv. Mater. 2018, 30, 1706344. [Google Scholar] [CrossRef]
- Bagheri, A.; Jin, J. Photopolymerization in 3D Printing. ACS Appl. Polym. Mater. 2019, 1, 593–611. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; McCarthy, E.D.; Soutis, C.; Cartmell, S.H. Lactone-layered double hydroxide networks: Towards self-assembled bioscaffolds. Appl. Clay Sci. 2018, 153, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Schimelman, J.; Wang, P.; Miller, K.L.; Ma, X.; You, S.; Guan, J.; Sun, B.; Zhu, W.; Chen, S. Photopolymerizable Biomaterials and Light-Based 3D Printing Strategies for Biomedical Applications. Chem. Rev. 2020, 120, 10695–10743. [Google Scholar] [CrossRef] [PubMed]
- Duval-Terrié, C.; Lebrun, L. Polymerization and Characterization of PMMA. Polymer Chemistry Laboratory Experiments for Undergraduate Students. J. Chem. Educ. 2006, 83, 443. [Google Scholar] [CrossRef]
- Ansong, O.E.; Jansen, S.; Wei, Y.; Pomrink, G.; Lu, H.; Patel, A.; Li, S. Accelerated controlled radical polymerization of methacrylates. Polym. Int. 2009, 58, 54–65. [Google Scholar] [CrossRef]
- Tsarevsky, N.V.; Sumerlin, B.S. (Eds.) Fundamentals of Controlled/Living Radical Polymerization; Royal Society of Chemistry: Cambridge, UK, 2013; pp. 1–59. [Google Scholar]
- Monteferrante, M.; Tiribocchi, A.; Succi, S.; Pisignano, D.; Lauricella, M. Capturing Free-Radical Polymerization by Synergetic Ab Initio Calculations and Topological Reactive Molecular Dynamics. Macromolecules 2022, 55, 1474–1486. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Wick, C.D.; Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 4. United-atom description of linear and branched alkenes and of alkylbenzenes. J. Phys. Chem. B 2000, 104, 8008–8016. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Poto, J.J.; Siepmann, J.I. Monte Carlo calculations for alcohols and their mixtures with alkanes. Transferable potentials for phase equilibria. 5. United-atom description of primary, secondary and tertiary alcohols. J. Phys. Chem. B 2001, 105, 3093–3104. [Google Scholar] [CrossRef]
- Stubbs, J.M.; Poto, J.J.; Siepmann, J.I. Transferable potentials for phase equilibria. 6. United-atom description for ethers, glycols, ketones and aldehydes. J. Phys. Chem. B 2004, 108, 17596–17605. [Google Scholar] [CrossRef]
- Kamath, G.; Robinson, J.; Poto, J.J. Application of TraPPE-UA force field for determination of vapor-liquid equilibria of carboxylate esters. Fluid Phase Equilibria 2006, 240, 46–55. [Google Scholar] [CrossRef]
- Maerzke, K.A.; Schultz, N.E.; Ross, R.B.; Siepmann, J.I. TraPPE-UA force field for acrylates and Monte Carlo simulations for their mixtures with alkanes and alcohols. J. Phys. Chem. B 2009, 113, 6415–6425. [Google Scholar] [CrossRef]
- Carbone, P.; Varzaneh, H.A.K.; Chen, X.; Müller-Plathe, F. Transferability of coarse-grained force fields: The polymer case. J. Chem. Phys. 2008, 128, 064904. [Google Scholar] [CrossRef]
- Peter, C.; Kremer, K. Multiscale simulation of soft matter systems–from the atomistic to the coarse-grained level and back. Soft Matter 2009, 5, 4357–4366. [Google Scholar] [CrossRef]
- D’Adamo, G.; Pelissetto, A.; Pierleoni, C. Predicting the thermodynamics by using state-dependent interactions. J. Chem. Phys. 2013, 138, 234107. [Google Scholar] [CrossRef] [PubMed]
- Gartner III, T.E.; Jayaraman, A. Modeling and simulations of polymers: A roadmap. Macromolecules 2019, 52, 755–786. [Google Scholar] [CrossRef] [Green Version]
- Chandran, S.; Baschnagel, J.; Cangialosi, D.; Fukao, K.; Glynos, E.; Janssen, L.M.; Müller, M.; Muthukumar, M.; Steiner, U.; Xu, J.; et al. Processing pathways decide polymer properties at the molecular level. Macromolecules 2019, 52, 7146–7156. [Google Scholar] [CrossRef]
- D’hooge, D.R.; Van Steenberge, P.H.; Reyniers, M.F.; Marin, G.B. The strength of multi-scale modeling to unveil the complexity of radical polymerization. Prog. Polym. Sci. 2016, 58, 59–89. [Google Scholar] [CrossRef]
- Odian, G. Principles of Polymerization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Modeling chemical reactions in classical molecular dynamics simulations. Polymer 2017, 128, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. REACTER: A Heuristic Method for Reactive Molecular Dynamics. Macromolecules 2020, 53, 9953–9961. [Google Scholar] [CrossRef]
- Orlandini, S.; Meloni, S.; Ciccotti, G. Hydrodynamics from statistical mechanics: Combined dynamical-NEMD and conditional sampling to relax an interface between two immiscible liquids. Phys. Chem. Chem. Phys. 2011, 13, 13177–13181. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [Green Version]
- Henderson, R. A uniqueness theorem for fluid pair correlation functions. Phys. Lett. A 1974, 49, 197–198. [Google Scholar] [CrossRef]
- de Oliveira, T.E.; Netz, P.A.; Kremer, K.; Junghans, C.; Mukherji, D. C–IBI: Targeting cumulative coordination within an iterative protocol to derive coarse-grained models of (multi-component) complex fluids. J. Chem. Phys. 2016, 144, 174106. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Katsoulakis, M.A.; Plecháč, P. Information-theoretic tools for parametrized coarse-graining of non-equilibrium extended systems. J. Chem. Phys. 2013, 139, 074115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, H.; Basu, S.; DeMeter, E.C. Molecular Dynamics Simulations of Photo-Induced Free Radical Polymerization. J. Chem. Inf. Model. 2020, 60, 6314–6327. [Google Scholar] [CrossRef]
- Torres-Knoop, A.; Kryven, I.; Schamboeck, V.; Iedema, P.D. Modeling the free-radical polymerization of hexanediol diacrylate (HDDA): A molecular dynamics and graph theory approach. Soft Matter 2018, 14, 3404–3414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meinel, M.K.; Müller-Plathe, F. Loss of molecular roughness upon coarse-graining predicts the artificially accelerated mobility of coarse-grained molecular simulation models. J. Chem. Theory Comput. 2020, 16, 1411–1419. [Google Scholar] [CrossRef]
- Ciccotti, G.; Jacucci, G. Direct computation of dynamical response by molecular dynamics: The mobility of a charged Lennard-Jones particle. Phys. Rev. Lett. 1975, 35, 789. [Google Scholar] [CrossRef]
- Ciccotti, G.; Jacucci, G.; McDonald, I. “Thought-experiments” by molecular dynamics. J. Stat. Phys. 1979, 21, 1–22. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, V.; Peralta, P.; Li, Y.; Oswald, J. A pressure-transferable coarse-grained potential for modeling the shock Hugoniot of polyethylene. J. Chem. Phys. 2016, 145, 104903. [Google Scholar] [CrossRef] [PubMed]
- Strauch, J.; McDonald, J.; Chapman, B.E.; Kuchel, P.W.; Hawkett, B.S.; Roberts, G.E.; Tonge, M.P.; Gilbert, R.G. Diffusion coefficients of the monomer and oligomers in hydroxyethyl methacrylate. J. Polym. Sci. Part Polym. Chem. 2003, 41, 2491–2501. [Google Scholar] [CrossRef]
- Milano, G.; Muller-Plathe, F. Mapping Atomistic Simulations to Mesoscopic Models: A Systematic Coarse-Graining Procedure for Vinyl Polymer Chains. J. Phys. Chem. B 2005, 109, 18609–18619. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285. [Google Scholar] [CrossRef]
- Tvorogov, N. The kinetic theory of gel formation in radical polymerization of polyfunctional unsaturated compounds. Polym. Sci. USSR 1976, 18, 2192–2202. [Google Scholar] [CrossRef]
- Potestio, R. Is Henderson’s theorem practically useful? JUnQ 2013, 3, 13–15. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteferrante, M.; Succi, S.; Pisignano, D.; Lauricella, M. Simulating Polymerization by Boltzmann Inversion Force Field Approach and Dynamical Nonequilibrium Reactive Molecular Dynamics. Polymers 2022, 14, 4529. https://doi.org/10.3390/polym14214529
Monteferrante M, Succi S, Pisignano D, Lauricella M. Simulating Polymerization by Boltzmann Inversion Force Field Approach and Dynamical Nonequilibrium Reactive Molecular Dynamics. Polymers. 2022; 14(21):4529. https://doi.org/10.3390/polym14214529
Chicago/Turabian StyleMonteferrante, Michele, Sauro Succi, Dario Pisignano, and Marco Lauricella. 2022. "Simulating Polymerization by Boltzmann Inversion Force Field Approach and Dynamical Nonequilibrium Reactive Molecular Dynamics" Polymers 14, no. 21: 4529. https://doi.org/10.3390/polym14214529