The Study on Structural and Photoelectric Properties of Zincblende InGaN via First Principles Calculation
Abstract
:1. Introduction
2. Method of Calculation
3. Results and Discussion
3.1. Lattice Constant
3.2. Band Structure
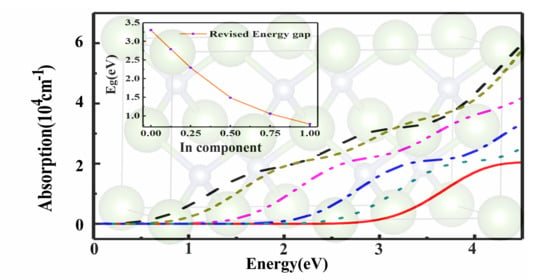
3.2.1. Correction of the Energy Gap
3.2.2. Mechanism of Bandgap Reduction and Bandgap Bowing Parameter
3.3. Density of States
3.4. Optical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Park, S.H.; Chuang, S.L. Comparison of zinc-blende and wurtzite GaN semiconductors with spontaneous polarization and piezoelectric field effects. J. Appl. Phys. 2000, 87, 353–364. [Google Scholar] [CrossRef]
- Xia, S.; Liu, L.; Diao, Y.; Fend, S. Doping process of p-type GaN nanowires: A first principle study. J. Appl. Phys. 2017, 122, 135102. [Google Scholar] [CrossRef]
- Pan, F.C.; Yang, B.; Lin, X.L. The Study of Magnetism in Un-doped 3C-GaN: The First-Principles Calculations. J. Supercond. Nov. Magn 2015, 28, 1617. [Google Scholar] [CrossRef]
- Khan, M.J.I.; Liu, J.; Hussain, S.; Usmani, M.N. First Principle Study of Optical Properties of Cu doped zincblende GaN for Novel Optoelectronic Applications. Optik 2020, 208, 164529. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Wu, L. The optical properties of GaN (001) surface modified by intrinsic defects from density functional theory calculation. Optik 2018, 154, 378. [Google Scholar] [CrossRef]
- Lu, Y.D.; Wang, L.W.; Zhang, Y. Properties of InGaN P-I-N ultraviolet detector. J. Semicond. Optoelectron. 2014, 35, 785. [Google Scholar]
- Kimura, R.; Shigemori, A.; Shike, J.; Ishida, K.; Takahashi, K. Improvement of cubic GaN film crystal quality by use of an AlN/GaN ordered alloy on GaAs (100) by plasma assisted molecular beam epitaxy. J. Cryst. Growth 2003, 251, 455. [Google Scholar] [CrossRef]
- Novikov, S.V.; Stanton, N.M.; Campion, R.P.; Morrist, R.D.; Kent, A.J. Growth and characterization of free-standing zinc-blende (cubic) GaN layers and substrates. Semicond. Sci. Technol. 2008, 23, 015018. [Google Scholar] [CrossRef]
- Liu, S.M.; Xiao, H.L.; Wang, Q.; Yan, J.D.; Zhan, X.M.; Gong, J.M.; Wang, X.L. InxGa1−xN/GaN Multiple Quantum Well Solar Cells with Conversion Efficiency of 3.77%. Chin. Phys. Lett. 2015, 32, 088401. [Google Scholar] [CrossRef]
- Jani, O.; Ferguson, I.; Honsberg, C.; Kurtz, S. Design and characterization of GaN/InGaN solar cells. Appl. Phys. Lett. 2007, 91, 132117. [Google Scholar]
- Neufeld, C.J.; Toledo, N.G.; Cruz, S.C.; Iza, M. High quantum efficiency InGaN/GaN solar cells with 2.95 eV band gap. Appl. Phys. Lett. 2008, 93, 1571. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 2003, 94, 3675. [Google Scholar] [CrossRef]
- Jia, W.L.; Zhou, M.; Wang, X.M.; Li, J.W. First-principles study on the optical properties of Fe-doped GaN. Chin. J. Phys. 2018, 67, 169. [Google Scholar]
- Lu, W. First-Principle Study of Electronic and Optical Properties of Wurtizite Structure GaN. Master’s Thesis, Xidian University, Xi’an, China, 2009. [Google Scholar]
- Shi, P. A Study on Transport Property of Cubic GaN Material and Its Heterojunction. Master’s Thesis, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Mullhauser, J.R.; Brandt, O.; Trampert, A.; Jenichen, B.; Ploog, K.H. Green photoluminescence from cubic In0.4Ga0.6N grown by radio frequency plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 1998, 73, 1230. [Google Scholar] [CrossRef]
- Goldhahn, R.; Scheiner, J.; Shokhovets, S.; Frey, T.; Kohler, U.; As, D.J.; Lischka, K. Refractive index and gap energy of cubic InxGa1−xN. Appl. Phys. Lett. 2000, 76, 291. [Google Scholar] [CrossRef]
- Wright, A.F.; Nelson, J.S. Bowing parameters for zinc-blende AlxGa1−xN and InxGa1−xN. Appl. Phys. Lett. 1995, 66, 3051. [Google Scholar] [CrossRef]
- Kou, Y.K.; Liou, B.T.; Yen, S.H.; Chu, H.Y. Vegard’s law deviation in lattice constant and band gap bowing parameter of zincblende InxGa1−xN. Opt. Commun. 2004, 237, 363. [Google Scholar]
- Ferhat, M.; Furthmuller, J.; Bechstedt, F. Gap bowing and Stoke shift in InxGa1−xN alloys: First-principles studies. Appl. Phys. Lett. 2002, 80, 1394. [Google Scholar] [CrossRef]
- Camacho, D.L.A.; Hopper, R.H.; Lin, G.M.; Myers, B.S.; Chen, A.B. Theory of AlN, GaN, InN and their alloys. J. Cryst. Growth 1997, 178, 8. [Google Scholar]
- Wu, J.; Walukiewicz, W.; Yu, K.M.; Ager, J.W., III; Haller, E.E.; Lu, H.; Schaff, W.J. Small band gap bowing in InxGa1−xN alloys. Appl. Phys. Lett. 2002, 80, 4741. [Google Scholar] [CrossRef]
- Caetano, C.; Teles, L.K.; Marques, L.M.; Ferreira, L.G. Phase stability, chemical bonds, and gap bowing of InxGa1−xN alloys: Comparison between cubic and wurtzite structures. Phys. Rev. B 2006, 74, 5215. [Google Scholar] [CrossRef] [Green Version]
- Marques, M.; Teles, L.K.; Scolfaro, L.M.R.; Leite, J.R.; Bechstedt, F. Lattice parameter and energy band gap of cubic AlxGayIn1−x−yN quaternary alloys. Appl. Phys. Lett. 2003, 83, 890. [Google Scholar] [CrossRef]
- Dridi, Z.; Bouhafs, B.; Roterana, P. First-principles investigation of lattice constants and bowing parameters in wurtzite AlxGa1-xN and InxAl1−xN alloys. Semicond. Sci. Technol. 2003, 18, 850. [Google Scholar] [CrossRef]
- Lei, T.; Moustakas, T.D.; Graham, R.J.; He, Y.; Berkowitz, S.J. Epitaxial growth and characterization of zinc-blende gallium nitride on (001) silicon. J. Appl. Phys. 1992, 71, 4933. [Google Scholar] [CrossRef]
- Perlin, P.; Jauberthie-Carillon, C.; Itie, J.P.; San, M.A.; Grzegory, I.; Polian, A. Raman scattering and x-ray-absorption spectroscopy ingallium nitride under high pressure. Phys. Rev. B 1992, 45, 83. [Google Scholar] [CrossRef]
- Davydov, V.Y.; Klochikhin, A.A.; Emtsev, V.V.; Kurdyukov, D.A.; Ivanov, S.V. Band gap of hexagonal InN and InGaN alloys. Phys. Stat. Sol. (b) 2002, 234, 787. [Google Scholar] [CrossRef] [Green Version]
- Bungaro, C.; Rapcewicz, K. Ab initio phonon dispersions of wurtzite AlN, GaN, and InN. Phys. Rev. B 2000, 61, 6720. [Google Scholar] [CrossRef] [Green Version]
- Ruan, X.X.; Zhang, F.C. First-Principles Investigation on Electronic Structure and Optical Properties of Wurtzite InxGa1−xN Alloys. Rare Met. Mat. Eng. 2015, 44, 3027. [Google Scholar]
- Huang, K. Solid State Physics; Higher Education Press: Beijing, China, 1988; pp. 49–70. [Google Scholar]
- Bernardini, F.; Fiorentini, V.; Vanderbilt, D. Spontaneous polarization and piezoelectric constants of III-V nitrides. Phys. Rev. B 1997, 56, 10024–10027. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Zhang, J.F. Nitride Wide Band Gap Semiconductor Materials and Electronic, 3rd ed.; Science Press: Beijing, China, 2013; pp. 66–86. [Google Scholar]
- Cesar, M.; Ke, Y.Q.; Ji, W.; Gou, H.; Mi, Z.T. Band gap of InxGa1−xN: A first principles analysis. Appl. Phys. Lett. 2011, 98, 202107. [Google Scholar] [CrossRef]
- Moses, P.G.; Walle, C.G.V. Band bowing and band alignment in InGaN alloys. Appl. Phys. Lett. 2010, 96, 3675. [Google Scholar] [CrossRef]
- Li, J.B. First Principles Study of Electronic Structure and Optical Properties of GaN Doping. Ph.D. Thesis, Xidian University, Xi’an, China, 2019. [Google Scholar]
- Zhang, Y.; Shao, X.H.; Wang, Z.Q. A first principle study on p-type doped 3C-SiC. Acta Phys. Sin. 2010, 59, 5652. [Google Scholar]
- Zheng, S.W.; Fan, G.H.; Zhang, T.; Su, C.; Song, J.J.; Ding, B.B. First-principles study on the energy bandgap bowing parameter of wurtzite BexZn1−xO. Acta Phys. Sin. 2013, 62, 305. [Google Scholar]
- Moses, P.G.; Miao, M.; Yan, Q.; Walle, C.G.V. Hybrid functional investigations of band gaps and band alignments for AlN, GaN, InN, and InGaN. J. Chem. Phys. 2011, 134, 084703. [Google Scholar] [CrossRef]
- Hassan, F.E.H.; Hashemifar, S.J.; Akbarzadeh, H. Density functional study of Zn1−xMgxSeyTe1-y quaternary semiconductor alloys. Phys. Rev. B 2006, 73, 195202. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Wang, Y.; Huang, Y.B.; Li, Z.H.; Yang, C. First principle study on the electronic and optical properties of AlxIn1−xAs. J. At. Mol. Phys. 2018, 36, 1057. [Google Scholar]
- Liu, X.F.; Luo, Z.J.; Zhou, X.; Wei, J.M.; Wang, Y.; Gou, X.; Lang, Q.Z.; Ding, Z. Calculation of electronic and optical properties of surface InxGa1−xP and indium-gradient structure on GaP (001). Comput. Mater. Sci. 2018, 153, 356. [Google Scholar] [CrossRef]
- Liu, X.F.; Ding, Z.; Lou, Z.J.; Zhou, X.; Wei, J.M.; Wang, Y.; Gou, X.; Lang, Q.Z. Theoretical study on the electronic and optical properties of bulk and surface (001) InxGa1−xAs. Physica B 2018, 537, 68. [Google Scholar] [CrossRef]
- Shen, X.C. Semiconductor Spectrum and Optical Properties, 2rd ed.; Science Press: Beijing, China, 2013; pp. 198–237. [Google Scholar]









| Indium Compositions | PSP/(C/m2) | Zincblende(nm) | Wurtzite(nm) | △L |
|---|---|---|---|---|
| 0 | −0.030, −0.029 [32,33] | 0.3217 | 0.3229 | 0.12% |
| 0.125 | −0.031 | 0.3262 | 0.3274 | 0.12% |
| 0.25 | −0.009 | 0.3297 | 0.3309 | 0.12% |
| 0.5 | 0.037 | 0.3394 | 0.3401 | 0.07% |
| 0.75 | −0.011 | 0.3476 | 0.3499 | 0.23% |
| 1 | −0.029, −0.032 [32,33] | 0.3573 | 0.3585 | 0.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Luo, Z.; Liu, X.; Li, E.; Jiang, C.; Huang, Z.; Li, J.; Guo, X.; Ding, Z.; Wang, J. The Study on Structural and Photoelectric Properties of Zincblende InGaN via First Principles Calculation. Crystals 2020, 10, 1159. https://doi.org/10.3390/cryst10121159
Song J, Luo Z, Liu X, Li E, Jiang C, Huang Z, Li J, Guo X, Ding Z, Wang J. The Study on Structural and Photoelectric Properties of Zincblende InGaN via First Principles Calculation. Crystals. 2020; 10(12):1159. https://doi.org/10.3390/cryst10121159
Chicago/Turabian StyleSong, Juan, Zijiang Luo, Xuefei Liu, Ershi Li, Chong Jiang, Zechen Huang, Jiawei Li, Xiang Guo, Zhao Ding, and Jihong Wang. 2020. "The Study on Structural and Photoelectric Properties of Zincblende InGaN via First Principles Calculation" Crystals 10, no. 12: 1159. https://doi.org/10.3390/cryst10121159