Multi-Hypothesis Marginal Multi-Target Bayes Filter for a Heavy-Tailed Observation Noise
Abstract
:1. Introduction
2. Background
2.1. MHMTB Filter
2.2. Models for Target Tracking
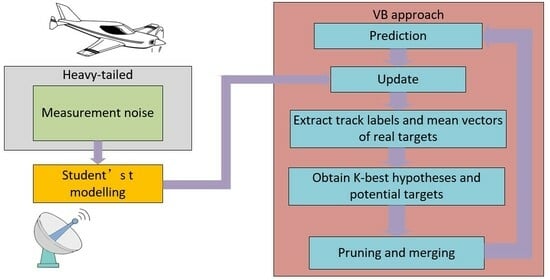
3. MHMTB Filter for a Heavy-Tailed Observation Noise
3.1. Prediction
3.2. Update
3.3. Obtaining K-Best Hypotheses and Potential Targets
| Algorithm 1: Acquiring the potential targets |
| set . . , , . end else if , , . end end end end , , , . end output: . |
3.4. Extracting the Track Labels and Mean Vectors of Real Targets
3.5. Pruning and Merging
| Algorithm 2: Extracting the track labels and mean vectors of real targets |
| set . , . , . end end . output: . |
| Algorithm 3: Pruning and merging |
| , . , , . . . , . repeat , (). . , . . , . , . . until . end output: . |
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Mahler, R. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Boston, MA, USA, 2014. [Google Scholar]
- Bar-Shalom, Y. Multitarget-Multisensor Tracking: Applications and Advances–Volume III; Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Yang, Z.; Li, X.; Yao, X.; Sun, J.; Shan, T. Gaussian process Gaussian mixture PHD filter for 3D multiple extended target tracking. Remote Sens. 2023, 15, 3224. [Google Scholar] [CrossRef]
- Li, Y.; Wei, P.; You, M.; Wei, Y.; Zhang, H. Joint detection, tracking, and classification of multiple extended objects based on the JDTC-PMBM-GGIW filter. Remote Sens. 2023, 15, 887. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, W.; Liu, Z. Student’s t-based robust Poisson multi-Bernoulli mixture filter under heavy-tailed process and measurement noises. Remote Sens. 2023, 15, 4232. [Google Scholar] [CrossRef]
- Liu, Z.X.; Chen, J.J.; Zhu, J.B.; Li, L.Q. Adaptive measurement-assignment marginal multi-target Bayes filter with logic-based track initiation. Digit. Signal Process. 2022, 129, 103636. [Google Scholar] [CrossRef]
- Du, H.; Xie, W.; Liu, Z.; Li, L. Track-oriented marginal Poisson multi-Bernoulli mixture filter for extended target tracking. Chin. J. Electron. 2023, 32, 1106–1119. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Trans. Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Tugnait, J.K.; Puranik, S.P. Tracking of multiple maneuvering targets using multiscan JPDA and IMM filtering. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 23–35. [Google Scholar]
- Mahler, R. Multitarget Bayes filtering via first-Order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.N.; Ma, W.K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Granstrom, K.; Orguner, U.; Mahler, R.; Lundquist, C. Extended target tracking using a Gaussian mixture PHD filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1055–1058. [Google Scholar] [CrossRef]
- Hu, Q.; Ji, H.B.; Zhang, Y.Q. A standard PHD filter for joint tracking and classification of maneuvering extended targets using random matrix. Signal Process. 2018, 144, 352–363. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Ji, H.B.; Hu, Q. A fast ellipse extended target PHD filter using box-particle implementation. Mech. Syst. Signal Process. 2018, 99, 57–72. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Ji, H.B.; Gao, X.B.; Hu, Q. An ellipse extended target CBMeMBer filter using gamma and box-particle implementation. Signal Process. 2018, 149, 88–102. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.L.; Gong, D.; Tang, B.T. Maneuvering multi-target tracking based on variable structure multiple model GMCPHD filter. Signal Process. 2017, 141, 158–167. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Hoang, H.G. An efficient implementation of the generalized labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Cao, C.H.; Zhao, Y.B.; Pang, X.J.; Suo, Z.L.; Chen, S. An efficient implementation of multiple weak targets tracking filter with labeled random finite sets for marine radar. Digit. Signal Process. 2020, 101, 102710. [Google Scholar] [CrossRef]
- Bryant, D.S.; Vo, B.T.; Vo, B.N.; Jones, B.A. A generalized labeled multi-Bernoulli filter with object spawning. IEEE Trans. Signal Process. 2018, 66, 6177–6189. [Google Scholar] [CrossRef]
- Wu, W.H.; Sun, H.M.; Cai, Y.C.; Jiang, S.R.; Xiong, J.J. Tracking multiple maneuvering targets hidden in the DBZ based on the MM-GLMB Filter. IEEE Trans. Signal Process. 2020, 68, 2912–2924. [Google Scholar] [CrossRef]
- Liang, Z.B.; Liu, F.X.; Li, L.Y.; Gao, J.L. Improved generalized labeled multi-Bernoulli filter for non-ellipsoidal extended targets or group targets tracking based on random sub-matrices. Digit. Signal Process. 2020, 99, 102669. [Google Scholar] [CrossRef]
- Liu, Z.X.; Chen, W.; Chen, Q.Y.; Li, L.Q. Marginal multi-object Bayesian filter with multiple hypotheses. Digit. Signal Process. 2021, 117, 103156. [Google Scholar] [CrossRef]
- Du, H.Y.; Wang, W.J.; Bai, L. Observation noise modeling based particle filter: An efficient algorithm for target tracking in glint noise environment. Neurocomputing 2015, 158, 155–166. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G.; Li, N.; Wu, Z.M.; Chambers, J.A. A novel robust Student’s t-based Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.L.; Leung, H.; Shen, K.; Wang, J.R. Student-t mixture labeled multi-Bernolli filter for multi-target tracking with heavy-tailed noise. Signal Process. 2018, 152, 331–339. [Google Scholar] [CrossRef]
- Zhu, H.; Leung, H.; He, Z.S. A variational Bayesian approach to robust sensor fusion based on Student-t distribution. Inf. Sci. 2013, 221, 201–214. [Google Scholar] [CrossRef]
- Li, W.L.; Jia, Y.M.; Du, J.P.; Zhang, J. PHD filter for multi-target tracking with glint noise. Signal Process. 2014, 94, 48–56. [Google Scholar] [CrossRef]
- Liu, Z.X.; Huang, B.J.; Zou, Y.N.; Li, L.Q. Multi-object Bayesian filter for jump Markov system under glint noise. Signal Process. 2019, 157, 131–140. [Google Scholar] [CrossRef]
- Miller, M.; Stone, H.; Cox, I. Optimizing Murty’s ranked assignment method. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 851–862. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. OSPA(2): Using the OSPA metric to evaluate multi-target tracking performance. In Proceedings of the International Conference on Control, Automation and Information Sciences (ICCAIS), Chiang Mai, Thailand, 31 October–1 November 2017; pp. 86–91. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]




| Target | Initial State | Appearing Time (s) | Disappearing Time (s) |
|---|---|---|---|
| 1 | 1 | 101 | |
| 2 | 10 | 101 | |
| 3 | 10 | 101 | |
| 4 | 10 | 101 | |
| 5 | 20 | 80 | |
| 6 | 40 | 101 | |
| 7 | 40 | 101 | |
| 8 | 40 | 80 | |
| 9 | 60 | 101 | |
| 10 | 60 | 101 |
| Filter | EIGLMB | MHMTB | VB-MHMTB | VB-EIGLMB |
|---|---|---|---|---|
| OSPA(2) error (m) | 41.7111 | 39.6084 | 31.2915 | 35.6949 |
| Cardinality error | 0.6257 | 0.4748 | 0.1330 | 0.2174 |
| Performing time (s) | 92.6159 | 3.6816 | 7.1489 | 111.2920 |
| 0.90 | 0.91 | 0.92 | 0.93 | 0.94 | 0.95 | 0.96 | 0.97 | 0.98 | 0.99 | 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| OSPA(2) error | 34.79 | 33.24 | 32.30 | 31.53 | 31.15 | 30.99 | 31.05 | 30.97 | 31.05 | 31.00 | 31.13 |
| Cardinality error | 0.130 | 0.127 | 0.128 | 0.129 | 0.128 | 0.129 | 0.136 | 0.131 | 0.132 | 0.129 | 0.137 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| OSPA(2) error | 40.65 | 34.51 | 31.75 | 30.58 | 32.10 | 32.32 | 33.05 | 35.46 | 37.44 |
| Cardinality error | 0.283 | 0.149 | 0.139 | 0.161 | 0.282 | 0.343 | 0.397 | 0.466 | 0.575 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Luo, J.; Zhou, C. Multi-Hypothesis Marginal Multi-Target Bayes Filter for a Heavy-Tailed Observation Noise. Remote Sens. 2023, 15, 5258. https://doi.org/10.3390/rs15215258
Liu Z, Luo J, Zhou C. Multi-Hypothesis Marginal Multi-Target Bayes Filter for a Heavy-Tailed Observation Noise. Remote Sensing. 2023; 15(21):5258. https://doi.org/10.3390/rs15215258
Chicago/Turabian StyleLiu, Zongxiang, Junwen Luo, and Chunmei Zhou. 2023. "Multi-Hypothesis Marginal Multi-Target Bayes Filter for a Heavy-Tailed Observation Noise" Remote Sensing 15, no. 21: 5258. https://doi.org/10.3390/rs15215258