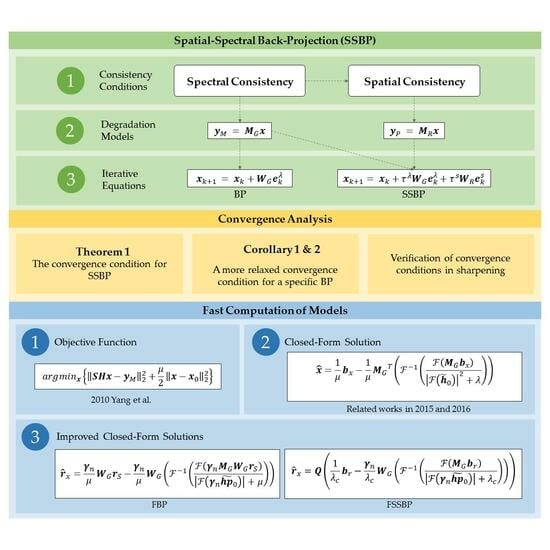
This section further develops the discussion on the acceleration of BP and SSBP algorithms, and two available routes for exploration are considered.
However, the computational procedure of this problem is not clear. First, although the first term in (26) yields a theoretically convergent solution based on the Drazin inverse, no efficient and feasible algorithm for finding the Drazin inverse has been found to exist. Secondly, the second term of the equation generates undesirable computational procedures when finding the partial sum of the matrix isometric series, i.e., it involves singular matrix inversion, leading to unreachable results. Finally, given that the dimensionality of is too high to explicitly declare it in the program, even if a theoretical solution can be obtained, it cannot be effectively applied to practical problems.
Therefore, this paper considers another idea: to associate the BP algorithm with the optimization problem. This means finding its equivalent or approximate objective function and exploring possible closed-form solutions for that objective function.
3.5.1. Fast BP
According to the relationship between BP and spectral consistency, the following ordinary least squares problem can be obtained from the spatial degradation process:
The term is often referred to as the data fidelity term, and the relationship between the gradient degradation of this formula and the BP algorithm can be established by setting the implicit initial solution conditions (set the iterative initial solution to be ), that is, the degradation transposition BP. However, due to the ill-posedness of the problem and the lack of regularization in the objective function, it is impossible to obtain numerically stable closed-form solutions only by relying on the data fidelity term (i.e., the globally optimal least-squares solution, which involves inverting the data matrix entries). Even if a regular term about itself (e.g., Tikhonov, total variational regularization, etc.) is added to the equation to stabilize the value, there is still the problem that the information related to is lost in the objective function because the least squares solution is independent of the initial solution setting. Therefore, it is necessary to append information to the regularization term.
Among them, (29) is actually the standard iterative formula of the BP algorithm, which is not directly related to (28). When is equal to , this formula corresponds to the gradient degradation of (27) with a step size of 1. Equation (30) is the gradient degradation corresponding to (28), where is the step-size parameter.
Although the above two formulas are similar in meaning, they are obviously not equivalent. Equation (28) can be regarded as an approximation of the objective function equivalent to the BP algorithm. Compared with (29), the additional term included in (30) will cause the variable update direction in the two equations to deviate from the second iteration (i.e., ). In the end, the two will also correspond to solutions under different objectives.
Since (28) is composed of two
problems, its closed-form solution exists theoretically. However, given the large size of the variables of interest (
) and the fact that it cannot be diagonalized in the frequency domain, that is, an equivalent implementation under Fourier transform cannot be sought, the closed-form solution is difficult to be derived directly. Fortunately, with the in-depth research on related problems, feasible closed-form solutions have been given in recent literatures [
30,
33], respectively. The core steps of the two proof ideas are to use the convolution theorem to convert the spatial domain convolution into the frequency domain dot product operation under the premise of making a periodic boundary assumption for the image, and through the Sherman–Morrison–Woodbury inversion formula, the
correlation representation is converted into
. The results obtained by the two are the same; the difference is that [
30] further obtains the convolution form of the key variables from the signal perspective by multiphase decomposition of the operations corresponding to
, while [
33] completes the derivation based on the matrix representation based on the relevant corollary of [
28]. According to the convolution representation in [
30], Equation (28) can correspond to the following closed-form solution:
where
,
and
represent forward and reverse fast Fourier transforms, respectively.
is the FIR filter corresponding to the
operation process, which is equivalent to the 0th polyphase component of
(computationally, it can be obtained by downsampling
), i.e.,
.
So far, the BP-related optimization problem as an approximation (Equation (28)) and a feasible closed-form solution to this problem (Equation (31)) have been clarified. However, it can be seen from the following that the performance of optimizing the sharpening method by the above process is not satisfactory, and no obvious quality improvement can be obtained compared to the sharpening initial solution. To this end, this paper further makes two improvements: one is to use variable substitution to convert the original problem into a residual representation for the objective function of (28); the other is to replace the projection filter equivalent to the degradation transpose in the closed-form solution with a general projection filter according to the design idea of the projection filter in BP.
- A.
Residual representation of objective function
Let
. Substituting into (28), the following optimization problem on
is obtained.
where
. The closed-form solution (31) is also changed accordingly to
After obtaining the , the required solution of the original problem is .
Although the above idea of solving based on variable substitution is equivalent to the solution of the original problem from the perspective of theoretical derivation, the actual results of both are not. The prerequisite for this closed-form solution is the assumption of the periodic boundary of the image; however, this assumption is usually not satisfied in the actual image. In contrast, the sparse nature of the residual images (obeying a Laplace distribution with zero mean) can mitigate the violation of this assumption.
Figure 3 shows the comparison of the sum of squared differences (SSD) between the reference image and the closed-form solution under both representations.
It can be clearly seen that the results based on the residual representation can greatly improve the error in the boundary parts of the image. It should be noted that the boundary error problem may also exist in the residual representation, and the degree of error is directly related to the setting of . A larger means a higher weight of the regular term and a smaller boundary error, but at the same time the difference with the BP objective function will be larger, which may cause a degradation of performance. With the same value setting, the results using the residual representation are always better than the results of the original image space representation. In fact, the boundary problem of sharpened results is common, for example, the most commonly used tap-23 filter also leads to some degree of boundary defects. Usually, a border crop is used by default (or a border padding) to remove the effect of this content. Therefore, the smaller the value, the more significant the performance improvement without affecting the boundary quality of the final output image. The residual representation can be more effective in reducing the reasonable range of values.
From the point of view of optimization objectives, (32) can also be understood as adding Tikhonov regularization (Tikhonov matrix is ) on the basis of the original data fidelity term on residuals, thereby replacing with during the derivative calculation. Since this process only adds a small perturbation to the diagonal elements of the latter, it means that the impact on the original objective function is relatively small. At the same time, the original information of is also retained outside the optimization problem and will not change with the optimization process, which is equivalent to the implicit inclusion of the initial solution in the gradient descent method. It is worth mentioning that the practice of using residual representation to improve performance is also widely used in deep convolutional network design. Although the starting point is different (the latter is used to improve the vanishing gradient phenomenon and increase the depth of the network), the basic logic in effect is the same.
- B.
Introducing General Spatial Projection Filter and Step Factor into Closed-Form Solution
On the basis of (33), the relevant variables of the interpolation stage are replaced with the relevant variables of the spatial projection filter. That is, to replace
and
with
and
, respectively, the solution at this time is
where
.
Note that when is the approximate ideal interpolation function mentioned earlier, and when is equivalent to the original closed-form solution corresponding to (33).
Different from (34), both (31) and (33) are derived from the derivation of the corresponding optimization objective functions. Due to the inclusion of -related terms, the latter two match the degradation transpose BP in terms of idea and performance. However, the purpose of this section is to form a more accurate approximation to BP while accelerating. Since the projection filter of BP itself has no actual physical meaning, it can theoretically be set arbitrarily under the condition of convergence, and it does not rule out the possibility of a better choice than degradation transpose. For example, in addition to degradation transpose projection filters, projection filters based on ideal interpolation can also be used. The following is a further analysis of the two types of filters.
First, the difference between the two is in the “shape” of the filter, or more importantly, in the Nyquist frequency to which the two correspond.
Figure 4 is an example of the interpolation results of the two filters, and the small picture in the upper left corner is the corresponding filter.
In principle, the interpolation process includes two stages of upsampling and low-pass filtering, wherein the purpose of the low-pass filtering operation is to remove the periodic repetition of the spectrum caused by the insertion of 0 samples in the upsampling stage. For digital images, approximate ideal interpolation functions (such as tap-23 commonly used for sharpening and tap-7 corresponding to bicubic) can make the image after the sampling rate increase as much as possible to keep the original signal samples unchanged. Intuitively speaking, the image should be enlarged to avoid blurring or other visual defects. The projection filter used in the degradation transpose BP is a
adapted to the MTF of the MS sensor with a Nyquist frequency typically around 0.3. If it is used in the interpolation process, there will be a loss of high-frequency information compared to the ideal interpolation function with a Nyquist frequency of 0.5. It can be seen from
Figure 4 that the result of the degenerate filter is slightly blurred compared to the ideal interpolation. Therefore, the ideal interpolation filter should be better than the degradation transpose filter in terms of interpolation principle. However, in terms of the entire BP process, the impact of this difference needs to be viewed dialectically. Considering that the projection operation is imposed on the error term
in the BP process (see (6)), it means that in each iteration process, the residual term of the degradation transpose BP is slightly more blurred than that of the ideal interpolation BP. On the one hand, if the unique details contained in
itself are not well preserved in
(as is the case with many sharpening algorithms) or there is useful detail compensation information in
due to the insufficient details injected by
from
, then the ideal interpolation BP will be more helpful to restore this part of detail than the “clear”
. On the other hand, if
or
contains some unnecessary detail defects (such as noise or aliasing) and appears in
, the relatively “fuzzy”
of degradation transpose BP can filter this part of the content, and the ideal interpolated BP may amplify the influence of these defects.
Second, the difference between the two projection filters is also reflected in the scaling of the coefficients. As mentioned above, the conventional interpolation filter (used in the ideal interpolation BP) is for the purpose of preserving energy (see
Section 3.3.2), and the sum of the coefficients is generally
times that of the degradation filter. In contrast, there is no magnification scaling between the interpolation and degradation filters of the degradation transpose BP (i.e., the scaling is 1). However, this does not imply that the degradation transpose BP is defective in energy preservation. In fact, according to the BP iterative formula of (6), since the projection filter acts on the error
, its coefficient magnification actually does not mainly involve the problem of maintaining the total energy of the image, but realizes the scaling of
. It is equivalent to playing the role of the step size factor in the iterative process, that is, the default step size of the degradation transpose BP and the ideal interpolation BP is 1 and
, respectively. In order to unify the operation between different filters and increase the variability, this paper further multiplies the closed-form solution of BP and the
-related variable (i.e.,
-related) in the iterative formula by a normalized step-size factor
, where
represents the accumulation of
coefficients. For the Fast BP (FBP), that is, (34) is adjusted accordingly as
Figure 5 shows the iterative convergence of the two BPs with different step size factors.
From
Figure 5, the following can be concluded:
(1) The effect of step size is consistent with the general iterative algorithm. The larger the step size, the faster the rate of residual decrease, but too large a step size may result in failure to obtain lower residuals or even non-convergence.
(2) The descent rate of the ideal interpolated BP is slightly higher than that of the degradation transpose BP when the same step factor is used and the convergence condition is satisfied, but the difference is not significant.
(3) The default step size of the degradation transpose BP () cannot achieve a reasonable degree of convergence in a small number of iterations, while the step size of the ideal interpolation BP () has the fastest convergence rate.
Therefore, combined with the consideration of the convergence conditions, the reasonable range of can be set to . Appropriately selecting a larger step size within a reasonable range is beneficial to obtain better comprehensive performance.
With the introduction of the step size factor, it is also equivalent to further increasing the variability of the projection filter settings. This is because the filters corresponding to different step sizes can be considered different (although only degenerate and ideal interpolation filter “shapes” are considered in this paper). Although the generic projection filter setting can no longer be derived from the optimal objective function, the modified solution is better suited from the point of view of finding a non-iterative fast solution that is as consistent as possible with the BP algorithm. Further change to other shapes of arbitrary filters satisfying the convergence condition is possible according to the actual demand.