A New Approach for Adaptive GPR Diffraction Focusing
Abstract
:1. Introduction
- (1)
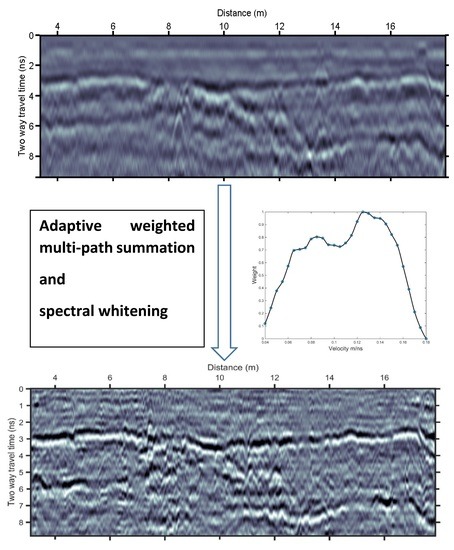
- Adaptive choice of the velocities range and the stacking weights used for the multipath summation. We achieved this by employing a “divide and conquer” algorithm, which does not require any user action. In addition, it significantly reduces the computational cost by avoiding unnecessary migration velocity tests (with zero weight in the stacking process).
- (2)
- Adaptive spectral scaling for the time-varying spectral whitening, which is applied on the output of the multipath summation process. The amplitude spectral scaling used here whitens the amplitude spectrum within the passband of the traces. This is based on the use of time-gated spectra of the signal in the t-f domain, without the need for applying band pass filtering.
2. Methodology
- Apply constant time-migration velocity scan of the GPR data using five specific velocity values covering the initial velocity range;
- Apply a divide and conquer approach [25] to find the velocity values, which have optimum contribution to the final summation of the migrated sections;
- Reapply constant time-migration velocity of the GPR data by using the velocity values not utilized in the previous steps [26];
- Stack the weighted migration sections [20];
- Apply adaptive spectrum scaling for time-varying spectral shaping of the multipath summation GPR section.
2.1. Evaluation of Constant Time-Migration Velocity Scan
2.2. Divide and Conquer Approach
2.3. Completing the Constant Time-Migration Velocity Scan
2.4. Stacking of Weighted Migration Sections
2.5. Applying Varying Spectral Shaping
3. Synthetic Example
4. Real Data
4.1. GPR Data Dominated by Reflections
4.2. GPR Data Dominated by Diffractions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Özdemir, C.; Demirci, F.; Yilit, E.; Yilmaz, B. A review on migration methods in B-Scan Ground penetrating radar imaging. Math. Probl. Eng. 2014, 2014, 280738. [Google Scholar] [CrossRef] [Green Version]
- Olhoeft, G.R. Electromagnetic field and material properties in ground penetrating radar. In Proceedings of the 2nd International Workshop on Advanced Ground Penetrating Radar, Delft, The Netherlands, 14–16 May 2003; pp. 144–147. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Arcone, S.; Fu, L.; Huang, Q. Radar wave scattering loss in a densely packed discrete random medium: Numerical modeling of a box-of-boulders experiment in the Mie regime. J. Appl. Geophys. 2013, 99, 68–75. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Y. Autofocusing Techniques for GPR Data from RC Bridge Decks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4860–4868. [Google Scholar] [CrossRef]
- Feng, D.; Li, T.; Li, G.; Wang, X. Reverse time migration of GPR data based on accurate velocity estimation and artifacts removal using total variation de-noising. J. Appl. Geophys. 2022, 198, 104563. [Google Scholar] [CrossRef]
- Sun, J.; Young, R. Recognizing surface scattering in ground-penetrating radar data. Geophysics 1995, 60, 1283–1597. [Google Scholar] [CrossRef]
- Özdemir, C.; Demirci, S.; Yigit, E. Practical Algorithms to Focus b-Scan GPR Images: Theory and Application to Real Data. Prog. Electromagn. Res. B 2008, 6, 109–122. [Google Scholar] [CrossRef] [Green Version]
- Bradford, J.H. Measuring water content heterogeneity using multi-fold GPR with reflection tomography. Vadose Zone J. 2008, 7, 184–193. [Google Scholar] [CrossRef]
- Bradford, J.H. Reverse-time prestack depth migration of GPR data from topography for amplitude reconstruction in complex environments. J. Earth Sci. 2015, 26, 791–798. [Google Scholar] [CrossRef]
- Forte, E.; Pipan, M. Review of multi-offset GPR applications: Data acquisition, processing and analysis. Signal Process. 2017, 132, 210–220. [Google Scholar] [CrossRef]
- Greaves, R.; Lesmes, D.; Lee, J.; Toksöz, M. Velocity variations and water content estimated from multi-offset ground-penetrating radar. Geophysics 1996, 61, 627–993. [Google Scholar] [CrossRef]
- Smitha, N.; UllasBharadwaj, D.R.; Abilash, S.; Sridhara, S.; Singh, V. Kirchhoff and F-K migration to focus ground penetrating radar images. Int. J. Geo-Eng. 2016, 7, 4. [Google Scholar] [CrossRef] [Green Version]
- Dou, Q.; Wei, L.; Magee, D.R.; Cohn, A.G. Real-Time Hyperbola Recognition and Fitting in GPR Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Yuan, H.; Montazeri, M.; Looms, M.; Nielsen, L. Diffraction imaging of ground-penetrating radar data. Geophysics 2019, 84, H1–H12. [Google Scholar] [CrossRef]
- Novais, A.; Costa, J.; Schleicher, J. GPR velocity determination by image-wave remigration. J. Appl. Geophys. 2008, 65, 65–72. [Google Scholar] [CrossRef]
- Clair, S.J.; Holbrook, W.S. Measuring snow water equivalent from common-offset GPR records through migration velocity analysis. Cryosphere 2017, 11, 2997–3009. [Google Scholar] [CrossRef] [Green Version]
- Fomel, S. Shaping regularization in geophysical estimation problems. Geophysics 2007, 72, R29–R36. [Google Scholar] [CrossRef]
- Landa, E.; Fomel, S.; Moser, T.J. Path-integral seismic imaging. Geophys. Prospect. 2006, 54, 491–503. [Google Scholar] [CrossRef]
- Merzlikin, D.; Fomel, S. Analytical path-summation imaging of seismic diffractions. Geophysics 2017, 82, S51–S59. [Google Scholar] [CrossRef]
- Economou, N.; Vafidis, A.; Bano, M.; Hamdan, H.; Ortega-Ramirez, J. Ground-penetrating radar data diffraction focusing without a velocity model. Geophysics 2020, 85, H13–H24. [Google Scholar] [CrossRef]
- Burnett, W.; Fomel, S.; Bansal, R. Diffraction velocity analysis bypath-integral seismic imaging. In Proceedings of the 81st Annual International Meeting, SEG, Expanded Abstracts, San Antonio, TX, USA, 18–22 September 2011; pp. 3898–3902. [Google Scholar]
- Schleicher, J.; Costa, J.C. Migration velocity analysis by double path-integral migration. Geophysics 2009, 74, WCA225–WCA231. [Google Scholar] [CrossRef] [Green Version]
- Santos, H.; Schleicher, J.; Novais, A.; Kurzmann, A.; Bohlen, T. Robust time-domain migration velocity analysis methods for initial-model building in a full waveform tomography workflow. In Proceedings of the 78th Annual International Conference and Exhibition, EAGE, Extended abstract, Vienne, Austria, 15–20 September 2019. [Google Scholar] [CrossRef]
- Economou, N.; Vafidis, A. GPR data time varying deconvolution by kurtosis maximization. J. Appl. Geophys. 2012, 81, 117–121. [Google Scholar] [CrossRef]
- Xia, G.; Sin, M.; Stoffa, P. 1-D Elastic Wave Inversion: A divide-and-conquer approach. Geophysics 1998, 63, 1670–1684. [Google Scholar] [CrossRef] [Green Version]
- Hamdan, H.; Economou, N.; Vafidis, A. Data Adaptive GPR Diffraction Focusing Using Multi-Path Summation. In Proceedings of the 26th European Meeting of Environmental and Engineering Geophysics, Online Conference, 7–8 December 2020; Volume 2020, pp. 1–5. [Google Scholar] [CrossRef]
- Bitri, A.; Grandjean, G. Frequency—Wavenumber modelling and migration of 2D GPR data in moderately heterogeneous dispersive media. Geophys. Prospect. 1998, 46, 287–301. [Google Scholar] [CrossRef]
- Claerbout, J.F. Earth Soundings Analysis: Processing versus Inversion, 1st ed.; Blackwell Scientific Publications: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hale, D. Local dip filtering with directional laplacians. GWP Proj. Rev. 2007, 567, 91–102. [Google Scholar]
- Cyganek, B. Object Detection and Recognition in Digital Images: Theory and Practice, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; p. 109. ISBN 9781118618363. [Google Scholar]
- Million, E. The Hadamard Product. 2007. Available online: http://buzzard.ups.edu/courses/2007spring/projects/million-paper.pdf (accessed on 1 October 2021).
- Economou, N.; Vafidis, A. Spectral balancing of GPR data using time-variant bandwidth in t-f domain. Geophysics 2010, 75, J19–J27. [Google Scholar] [CrossRef]
- Economou, N.; Vafidis, A. Deterministic deconvolution for GPR data in t-f domain. Near Surf. Geophys. 2011, 9, 427–433. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S-transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Sandmeier, K. Reflex Manual 2019; Version 9.0; Sandmeier Geophysical Research: Karlsruhe, Germany, 2019; Available online: www.sandmeier-geo.de (accessed on 1 April 2021).
- Economou, N.; Bano, M.; Ortega-Rameriz, J. Delineation of Fractures Using a 2D GPR Processing Strategy for 3D Imaging: Weak Zones within Carbonates at the Archaeological Site of Xochicalco in Mexico. Appl. Sci. 2021, 11, 5893. [Google Scholar] [CrossRef]
- Ruiz-Violante, A.; Basañez-Loyola, M. La Formacion Xochicalco, Unidad estratigráfica del Albiano-Cenomanianoenlos Estados de Morelos, Guerrero y México. In Proceedings of the XII Convención Geológica Nacional, Sociedad Geológica Mexicana, Toluca, Mexico, 1994; pp. 161–162. [Google Scholar]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdan, H.; Economou, N.; Vafidis, A.; Bano, M.; Ortega-Ramirez, J. A New Approach for Adaptive GPR Diffraction Focusing. Remote Sens. 2022, 14, 2547. https://doi.org/10.3390/rs14112547
Hamdan H, Economou N, Vafidis A, Bano M, Ortega-Ramirez J. A New Approach for Adaptive GPR Diffraction Focusing. Remote Sensing. 2022; 14(11):2547. https://doi.org/10.3390/rs14112547
Chicago/Turabian StyleHamdan, Hamdan, Nikos Economou, Antonis Vafidis, Maksim Bano, and Jose Ortega-Ramirez. 2022. "A New Approach for Adaptive GPR Diffraction Focusing" Remote Sensing 14, no. 11: 2547. https://doi.org/10.3390/rs14112547