Mineral Exploration Potential Estimation Using 3D Inversion: A Comparison of Three Different Norms
Abstract
:1. Introduction
2. Methods
2.1. Closed-Form Solution of Gravity Field
2.2. Principles of Inversion Approaches
2.3. Bound Constraint
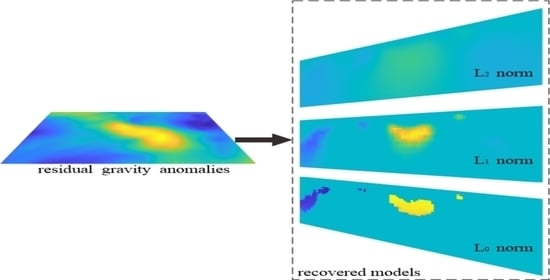
3. Results
3.1. Synthetic Data Examples
3.2. Real Data Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G.; Huang, L. 3D geological modeling for mineral resource assessment of the Tongshan Cu deposit, Heilongjiang Province, China. Geosci. Front. 2012, 3, 483–491. [Google Scholar] [CrossRef] [Green Version]
- Mery, N.; Emery, X.; Cáceres, A.; Ribeiro, D.; Cunha, E. Geostatistical modeling of the geological uncertainty in an iron ore deposit. Ore Geol. Rev. 2017, 88, 336–351. [Google Scholar] [CrossRef]
- Silva, D.; Almeida, J. Geostatistical methodology to characterize volcanogenic massive and stockwork ore deposits. Minerals 2017, 7, 238. [Google Scholar] [CrossRef] [Green Version]
- Lamamra, A.; Neguritsa, D.L.; Mazari, M. Geostatistical modeling by the Ordinary Kriging in the estimation of mineral resources on the Kieselguhr mine, Algeria. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012051. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Zhu, Z.X.; Yan, J.D. The application of SD method in mineral resources reserves calculation in the Jiguanzi Copper-gold deposit, Daye, Hubei province. Geol. Explor. 2004, 40, 82. [Google Scholar]
- Battalgazy, N.; Madani, N. Categorization of mineral resources based on different geostatistical simulation algorithms: A case study from an iron ore deposit. Nat. Resour. Res. 2019, 28, 1329–1351. [Google Scholar] [CrossRef]
- Truong, X.L.; Truong, X.Q.; Nguyen, T.A.; Raghavan, V.; Nguyen, C.C. Development of HUMGEOSTAT: A new geological tool for geostatistical analysis of mineral deposit: A case study at sin Quyen mine (northern Vietnam). J. Geol. Soc. India 2019, 93, 574–582. [Google Scholar] [CrossRef]
- Wellmer, F.W.; Dalheimer, M.; Wagner, M. Economic Evaluations in Exploration, 2nd ed.; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Erarslan, K. Computer aided ore body modelling and mine valuation. Earth Sci. 2012, 16, 345–372. [Google Scholar]
- Onur, A.H.; Konak, G.; Karakuş, D. Limestone quarry quality optimization for a cement factory in Turkey. J. South. Afr. Inst. Min. Metall. 2008, 108, 751–757. [Google Scholar]
- Xu, S.; Sirieix, C.; Marache, A.; Riss, J.; Malaurent, P. 3D geostatistical modeling of Lascaux hill from ERT data. Eng. Geol. 2016, 213, 169–178. [Google Scholar] [CrossRef]
- Gao, X.; Xiong, S.; Yu, C.; Zhang, D.; Wu, C. The Estimation of Magnetite Prospective Resources Based on Aeromagnetic Data: A Case Study of Qihe Area, Shandong Province, China. Remote Sens. 2021, 13, 1216. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Meng, Z. Three-dimensional potential field data inversion with L0 quasinorm sparse constraints. Geophys. Prospect. 2018, 66, 626–646. [Google Scholar] [CrossRef]
- Sun, Y.; Schaefer, S.; Wang, W. Denoising point sets via L0 minimization. Comput. Aided Geom. Des. 2015, 35, 2–15. [Google Scholar] [CrossRef]
- Hyder, M.; Mahata, K. An approximate l0 norm minimization algorithm for compressed sensing. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, China, 19–24 April 2009; pp. 3365–3368. [Google Scholar]
- Sun, Y.; Tao, J. Image reconstruction from few views by ℓ0-norm optimization. Chin. Phys. B 2014, 23, 078703. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.; Ni, M.; Zhu, Q.; Sun, C.; Kang, L. L0-norm sparse representation based on modified genetic algorithm for face recognition. J. Vis. Commun. Image Represent. 2015, 28, 15–20. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W.; Feng, J.; Liu, F.; Yu, H. Low-dose spectral CT reconstruction based on image-gradient L0-norm and adaptive spectral PICCS. Phys. Med. Biol. 2020, 65, 245005. [Google Scholar] [CrossRef]
- Chen, G.; Chen, S.; Wang, H.; Zhang, B. Geophysical data sparse reconstruction based on L0-norm minimization. Appl. Geophys. 2013, 10, 181–190. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, Y.; Zheng, Y.; Wu, S.; Chang, X.; Zhu, W. Electrical resistivity tomography with smooth sparse regularization. Geophys. Prospect. 2021, 69, 1773–1789. [Google Scholar] [CrossRef]
- Yang, J.; Yin, C.; Dai, R.; Yang, S.; Zhang, F. Seismic impedance inversion via L0 gradient minimisation. Explor. Geophys. 2019, 50, 575–582. [Google Scholar] [CrossRef]
- Last, B.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef] [Green Version]
- Ghalehnoee, M.; Ansari, A.; Ghorbani, A. Improving compact gravity inversion based on new weighting functions. Geophys. J. Int. 2016, 208, 546–560. [Google Scholar] [CrossRef]
- Meng, Z.; Xu, X.; Huang, D. Three-dimensional gravity inversion based on sparse recovery iteration using approximate zero norm. Appl. Geophys. 2018, 15, 524–535. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Utsugi, M. Magnetic inversion to recover the subsurface block structures based on L1 norm and total variation regularization. Geophys. J. Int. 2022, 228, 510–537. [Google Scholar] [CrossRef]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Talwani, M.; Ewing, M. Rapid computation of gravitational attraction of three-dimensional bodies of arbitrary shape. Geophysics 1960, 25, 203–225. [Google Scholar] [CrossRef]
- Paul, M.K. The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure Appl. Geophys. 1974, 112, 553–561. [Google Scholar] [CrossRef]
- Okabe, M. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics 1979, 44, 730–741. [Google Scholar] [CrossRef]
- Haáz, I.B. Relations between the potential of the attraction of the mass contained in a finite rectangular prism and its first and second derivatives. Geophys. Trans. II 1953, 7, 57–66. [Google Scholar]
- Li, X.; Chouteau, M. Three-dimensional gravity modeling in all space. Surv. Geophys. 1998, 19, 339–368. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat.-Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G. Forward modeling of gravity anomalies based on cell mergence and parallel computing. Comput. Geosci. 2018, 120, 1–9. [Google Scholar] [CrossRef]
- Chen, T.; Yang, D. Modeling and Inversion of Airborne and Semi-Airborne Transient Electromagnetic Data with Inexact Transmitter and Receiver Geometries. Remote Sens. 2022, 14, 915. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef] [Green Version]
- Hanke, M. Limitations of the L-curve method in ill-posed problems. BIT Numer. Math. 1996, 36, 287–301. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Grayver, A.V.; Streich, R.; Ritter, O. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver. Geophys. J. Int. 2013, 193, 1432–1446. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yao, C.; Zheng, Y.; Wang, J.; Zhang, Y. 3D magnetic sparse inversion using an interior-point method. Geophysics 2018, 83, J15–J32. [Google Scholar] [CrossRef]
- Rao, B.D.; Kreutz-Delgado, K. An affine scaling methodology for best basis selection. IEEE Trans. Signal Process. 1999, 47, 187–200. [Google Scholar] [CrossRef] [Green Version]
- Lau, A.; Yin, C. L0 + L1 + L2 mixed optimization: A geometric approach to seismic imaging and inversion using concepts in topology and semigroup. arXiv 2010, arXiv:1007.1880. [Google Scholar]
- Li, Y.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef] [Green Version]
- Chen, S. Gravity Exploration, 1st ed.; Geological Publishing House: Beijing, China, 1987; pp. 272–283. (In Chinese) [Google Scholar]
- Zeng, H.; Xu, D.; Tan, H. A model study for estimating optimum upward continuation height for gravity separation with application to a Bouguer gravity anomaly over a mineral deposit, Jilin province, northeast China. Geophysics 2007, 72, I45–I50. [Google Scholar] [CrossRef]
- Guo, L.; Meng, X.; Chen, Z.; Li, S.; Zheng, Y. Preferential filtering for gravity anomaly separation. Comput. Geosci. 2013, 51, 247–254. [Google Scholar] [CrossRef]
- GeoGoku. Available online: https://github.com/GeoGoku (accessed on 12 April 2022).
- Chen, T.; Yang, D. Potential field data interpolation by Taylor series expansion. Geophysics 2022, 87, G15–G27. [Google Scholar] [CrossRef]
- Zeng, H. Gravity Field and Gravity Exploration, 1st ed.; Geological Publishing House: Beijing, China, 2005; pp. 251–254, (In Chinese with English Contents). [Google Scholar]












| Model Norm | Noise Level (mGal) | Time (s) | Exploration Potential (tons) |
|---|---|---|---|
| L2 | 1.10 × 10−2 | 139 | 5.20 × 107 |
| L1 | 6.00 × 10−3 | 512 | 1.71 × 107 |
| L0 | 5.20 × 10−3 | 431 | 1.01 × 107 |
| Model Norm. | Noise Level (mGal) | Time (s) | Exploration Potential (tons) |
|---|---|---|---|
| L2 | 1.03 × 10−2 | 106 | 5.57 × 106 |
| L1 | 7.30 × 10−3 | 412 | 5.36 × 106 |
| L0 | 5.50 × 10−3 | 549 | 2.32 × 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Zhang, G. Mineral Exploration Potential Estimation Using 3D Inversion: A Comparison of Three Different Norms. Remote Sens. 2022, 14, 2537. https://doi.org/10.3390/rs14112537
Chen T, Zhang G. Mineral Exploration Potential Estimation Using 3D Inversion: A Comparison of Three Different Norms. Remote Sensing. 2022; 14(11):2537. https://doi.org/10.3390/rs14112537
Chicago/Turabian StyleChen, Tao, and Guibin Zhang. 2022. "Mineral Exploration Potential Estimation Using 3D Inversion: A Comparison of Three Different Norms" Remote Sensing 14, no. 11: 2537. https://doi.org/10.3390/rs14112537