Next Article in Journal
Oil in Water Nanoemulsions Loaded with Tebuconazole for Populus Wood Protection against White- and Brown-Rot Fungi
Next Article in Special Issue
Effect of Charcoal on the Properties, Enzyme Activities and Microbial Diversity of Temperate Pine Forest Soils
Previous Article in Journal
Genome-Wide Characterization of HSP90 Gene Family in Malus sieversii and Their Potential Roles in Response to Valsa mali Infection
Previous Article in Special Issue
Warming Increases the Carbon Sequestration Capacity of Picea schrenkiana in the Tianshan Mountains, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 12
Issue 9
10.3390/f12091233
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Prediction of the Carbon Content of Six Tree Species from Visible-Near-Infrared Spectroscopy

by
Yongbin Meng
1,†,
Yuanyuan Zhang
2,†,
Chunxu Li
1,
Jinghan Zhao
1,
Zichun Wang
1,
Chen Wang
1 and
Yaoxiang Li
1,*
1
College of Engineering and Technology, Northeast Forestry University, Harbin 150040, China
2
College of Chemistry, Chemical Engineering and Resource Utilization, Northeast Forestry University, Harbin 150040, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work (Co-first author).
Forests 2021, 12(9), 1233; https://doi.org/10.3390/f12091233
Submission received: 15 July 2021 / Revised: 2 September 2021 / Accepted: 8 September 2021 / Published: 10 September 2021
(This article belongs to the Special Issue Carbon Stock and Sequestration in Forest Ecosystems)
Browse Figures
Versions Notes

Abstract

:
This study aimed to measure the carbon content of tree species rapidly and accurately using visible and near-infrared (Vis-NIR) spectroscopy coupled with chemometric methods. Currently, the carbon content of trees used for calculating the carbon storage of forest trees in the study of carbon sequestration is obtained by two methods. One involves measuring carbon content in the laboratory (K2CrO7-H2SO4 oxidation method or elemental analyzer), and another involves directly using the IPCC (Intergovernmental Panel on Climate Change) default carbon content of 0.45 or 0.5. The former method is destructive, time-consuming, and expensive, while the latter is subjective. However, Vis-NIR detection technology can avoid these shortcomings and rapidly determine carbon content. In this study, 96 increment core samples were collected from six tree species in the Heilongjiang province of China for analysis. The spectral data were preprocessed using seven methods, including extended multiplicative scatter correction (EMSC), first derivative (1D), second derivative (2D), baseline correction, de-trend, orthogonal signal correction (OSC), and normalization to eliminate baseline drifting and noise, as well as to enhance the model quality. Linear models were established from the spectra using partial least squares regression (PLS). At the same time, we also compared the effects of full-spectrum and reduced spectrum on the model’s performance. The results showed that the spectral data processed by 1D with the full spectrum could obtain a better prediction model. The 1D method yielded the highest R2c of 0.92, an RMSEC (root-mean-square error of calibration) of 0.0056, an R2p of 0.99, an RMSEP (root-mean-square error of prediction) of 0.0020, and the highest RPD (residual prediction deviation) value of 8.9. The results demonstrate the feasibility of Vis-NIR spectroscopy coupled with chemometric methods in determining the carbon content of tree species as a simple, rapid, and non-destructive method.

Graphical Abstract

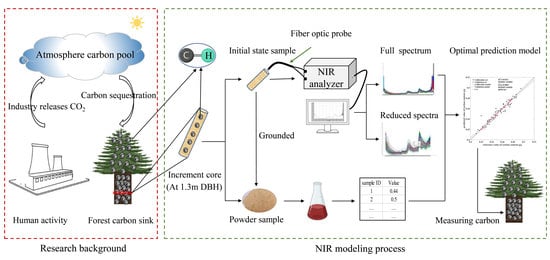
1. Introduction

Increased CO2 levels result in global warming and frequent natural disasters, which represent a series of positive feedback effects [1,2,3]. As the largest ecosystem on land, forests play a vital role in the global carbon cycle and represent a vast carbon reservoir [4]. Forest carbon stock accounts for about 45–54% of the total C in terrestrial ecosystems [5]. At present, there are many methods for estimating carbon reserves in forest trees, but biomass remains the most widely used, direct, and accurate method [6]. Forest-tree carbon reserves are usually calculated by multiplying biomass with the carbon content of vegetation biomass. Therefore, the carbon content of tree species and biomass are two critical factors used to quantify carbon storage in forest ecosystems. In past studies, more attention was paid to biomass estimation while ignoring the carbon content. In this method, the general calculation process takes a fixed value of 0.5 or 0.45 [7,8,9], but the carbon contents of different tree species and the same tree species in different regions and during different seasons differ significantly [10,11,12]. Dong L.H. et al. researched the carbon content of 10 broadleaf species in natural forests in northeast China and observed significantly different carbon contents among the tree species [13]. Marín P. G. et al. measured the carbon content of 175 species in Mexican forests and found that tree species from different biomes significantly differed in their carbon contents (42.8% to 44.3% for species from the tropics and subtropics and from 43.8% to 44.2% for species in arid and semiarid zones; F = 9.07, p = 0.0002) [14]. Therefore, to a certain extent, using a fixed value for estimating the stand carbon pool will cause a great deviation. Assuming a global carbon content of 50% led to overestimating the total carbon stocks by between 4.1% and 5.6% [15]. One study showed that the generalized assumption of 50% C content is consistently slightly above the real values for the species studied. Though small in some cases, this overestimation could lead to errors of 3.9 Mg ha−1 in some Mexican forests [14]. Therefore, it is essential to determine the carbon content of different tree species when calculating carbon storage.
The most common methods for measuring the carbon content of tree species are the dry combustion method (element analyzer) [10,12] and the wet combustion method (K2CrO7-H2SO4 oxidation method) [16]. The former method is simple and relatively accurate but expensive, while the latter requires significant time, energy, and chemicals. Both methods have a common disadvantage in that they require crushing of the sample. Therefore, these methods are not suitable for detecting the carbon sink dosage for large numbers of the sample. Therefore, in light of developments in green technology, there is a critical need to find a simple and rapid method for detecting carbon content to meet the precise metrics needed under the dynamic changes of carbon sinks. Alternatively, near-infrared spectroscopic detection techniques seem most appropriate.
Vis-NIRS is a green, eco-friendly, simple, and effective qualitative and quantitative spectroscopic analytical technology [17]. Coupled with suitable chemometric methods, NIR has been successfully applied in many fields such as the petrochemical [18,19], agricultural [20,21,22], food [17,23,24], pharmaceutical [25], and traditional Chinese medicine industries [26]. In recent years, Vis-NIR has also shown great potential in forestry applications [27,28,29,30]. Wood spectroscopy relies on the fact that the fraction of reflected light received by the instrument at any given wavelength (typically between 350 and 2500 nm in the visible and near-infrared parts of the spectrum) relates to the vibrational and rotational states of molecules containing oxygen, hydrogen, carbon, or nitrogen atoms. The recorded spectrum is then used to derive a statistical model that relates the wood’s properties to spectral information. Such spectroscopic models have been derived from a wide range of wood attributes, especially those related to organic molecules and the physical properties of wood, such as wood lignin content, wood density, and the bending strength of wood. Li Ying et al. applied Vis-NIRS and chemometric methods to accomplish wood-density predictions and origin/species identification [31,32]. Steffen Herrmann’s research results showed that NIRS models were suitable for predicting concentrations of C, N, P, lignin, and extractives of coarse woody debris [33]. Oliver Elle et al. used CARS-PLS (competitive adaptive reweighted sampling and PLS) to select the most relevant wavelengths for root lignin prediction [34]. Xiao Li determined hemicellulose, cellulose, and lignin in Moso Bamboo via near-infrared spectroscopy [35]. NIRS is also used to predict element content. For example, Francisco J.A. et al. showed that the precision of the resulting NIR method meets international requirements, indicating that one NIR measurement scan of a foliar sample can predict the sample’s N, P and C content with precision based on the standard method’s performance [36]. These studies show that Vis-NIRS could be a potential tool to predict the carbon content of tree species. To the best of our knowledge, there is no report on using a combination of NIR spectroscopy and chemometrics to discriminate and quantify carbon content in tree species. Therefore, we propose a hypothesis: Near-infrared spectroscopy can be used to detect the carbon content of tree species.
However, near-infrared spectroscopy cannot be directly used for quantitative detection, so it needs to be combined with chemometrics to establish a prediction model. Partial least squares (PLS) is the most common method used for quantitative analysis in near-infrared spectroscopy. Hou R. et al. [37] established a prediction model of protein content using PLS to determine the near-infrared spectra of 58 barley samples. The prediction correlation coefficient was 0.901. Marcelo A. studied using a combination of NIR PLS to determine the total protein content in raw coffee samples [38]. Using the PLS method, Kensuke K. et al. established the near-infrared prediction model of soil carbon content [39]. Many other studies establish a near-infrared quantitative prediction model via PLS regression [40,41,42,43].
Moreover, the Vis-NIR spectra at 350–2500 nm are broad, with overlapping bands, and the relationship between spectra and wood properties is generally complex and nonspecific. Meanwhile, the instrument response, stray light, light scattering, sample state, and other factors also commonly affect the determination of the original image data from near-infrared spectroscopy. Near-infrared spectroscopy data inevitably contain noise, such as random, baseline drift, and instrument background noise, which will affect the analysis of near-infrared spectroscopy data. Therefore, the pretreatment of spectral data is very important. In a study by James et al., the OSC method improved prediction accuracy (R2CV = 0.79; without OSC, the best result was R2CV = 0.62) [44]. Yin et al. [45] determined the basic density of Tilia tuan based on different pretreatments the results showed that the first derivative was optimal in the range of 350–2500 nm. The correlation coefficient of the calibration set was 0.9648, the corrected root mean square error was 0.0027, and the correlation coefficient of the verification set was 0.9432. Other models with good predictive performance use different spectral pretreatment methods, such as multiplicative scatter correction, Standard Normal Variate, and second derivative [21,46,47,48,49].
Our study collected the spectral information and carbon content of 96 trunk increment core samples from six tree species in two different ecological regions, using the seven spectral pretreatment methods, and established near-infrared quantitative models through partial least squares regression. We also examined the effects of full-spectrum and reduced spectrum on the performance of the model. This study is intended to establish a better performing quantitative model for predicting the carbon content of tree species. For this study, we sought to answer two main questions: (1) What spectral pretreatment method combined with PLS can best predict the carbon content of tree species? (2) Between the full spectrum and reduced spectrum, which spectrum is most suitable for modeling and predicting the carbon content of tree species?

2. Materials and Methods

2.1. Sample Preparation

The samples were collected from 96 trunk increment core samples from 6 tree species (Diameter at Breast Height position at 1.3 m) in two different ecological regions. Two species were Betula platyphylla and Larix gmelinii from the Xinlin forest farm (geographical coordinates: 123°41′–125°25′ E, 51°20′–52°10′ N) in the Greater Khingan Mountains of Heilongjiang Province, China. The other four species were Picea asperata Mast., Abies fabri (Mast.) Craib, Acer pictum Thunb. ex Murray, and Acer tegmentosum Maxim. from the Dong fanghong forest farm (geographical coordinates: 129°5.150′–129°5.205′ E, 46°52.511′–46°52′ N) of Dailing Forestry Bureau in the Xiaoxing anling area of Heilongjiang Province, China. Active clay was used to fill the holes left after sampling the growing cone to help the trees heal themselves and prevent infection from insects and microorganisms. First, the increment core samples were naturally dried in the shade, and the spectra were collected. The samples were then dried at a constant temperature in a drying oven (85 °C) to a constant weight, crushed, and sieved to analyze their carbon content chemically.

2.2. Carbon Content Based on Chemical Analysis

The increment core samples were dried to a constant weight in a drying oven with a constant temperature of 85 °C; the difference between the two weights was less than 0.2 mg. The samples were then ground and sieved (0.25 mm mesh screen). The carbon content was determined and calculated via the potassium dichromate wet burning sulfuric acid oxidation method (LY/T1237-1999) [50]. During the experiment, the oil bath temperature was controlled at 170–180 °C, and the accuracy time was 5 minutes. Three replicates were determined for each sample, and the relative deviation of the three replicates was controlled within 2%. If the average relative error exceeded ±2%, we repeated the process once more and retained the average of three determination results with the smallest difference as the carbon content of the sample. The determination results of the carbon content are shown in Table 1.

2.3. Spectra Collection

The Vis-NIR spectra were collected using a LabSpec Pro FR/A114260 (Analytical Spectral Devices, Inc., Boulder, CO, USA) from 350 to 2500 nm with a spectral resolution of 3 nm @700 nm and 10 nm @1400/2100 nm. To ensure the accuracy of the data, the experiment was carried out under drying conditions at room temperature. Before spectral collection, the spectrometer was preheated for 30 min and calibrated with a commercial white plate made from polytetrafluoroethylene (PTFE). This plate was nearly 100% reflective within the whole wavelength range (350–2500 nm). White references were collected every 15 min from the surface of the white plate. In total, 30 scans were acquired and automatically averaged into one spectrum. Each sample was then scanned three times with a glare probe (unit 6523 h.i. for the contact probe), and the average spectrum was considered the raw spectrum [31]. The signals were generated in the reflectance mode and transformed into absorbance using log1/R.
The sample was truncated from the middle position of the wood to collect the spectrum. To obtain a more stable model, each wood sample was polished with 80 mesh sandpaper five times such that the surface roughness parameter, Ra, was close to 12.5 μm. According to the research of Jiang Z. H. et al. [51] and Evelize A. [29], the information contained in the near-infrared spectra of the three sections of wood samples can be used to characterize wood samples, and the information content is rich. According to the characteristics of the experimental materials, the cross-section of the wood sample was selected to collect the near-infrared spectrum (Figure 1a). The spectrum collected by this method was the spectrum of the tangential section of the wood at the DBH position of the tree (Figure 1b). The near-infrared spectra of each sample are shown in Figure 2.

2.4. Pre-Processing of Spectroscopic Data

Vis-NIR spectroscopy provides a great deal of information about tree species along wavelengths of 350 and 2500 nm. However, instrument responses, stray light, light scattering, the sample state, and other factors usually affect the determination of the original image data of near-infrared spectroscopy. Therefore, it is essential to preprocess the spectral data before modeling. The primary function of all preprocessing methods is to reduce unmodeled variability in the data and enhance the features sought in the spectra, which are often linear (simple) relations. However, choosing the most robust preprocessing technique can be challenging because applying a wrong type or applying a preprocessing method that is too severe can result in the removal of valuable information or even the introduction of unwanted variation. Before NIR modeling, the spectra were subjected to pretreatments, including EMSC, 1D, 2D, Baseline correction, de-trend, OSC, and normalization to eliminate baseline drifting and noise and enhance the model quality. EMSC eliminates the multiplicative and additive effects of spectra and allows a better separation of physical light scattering effects from chemical light absorbance effects. Derivative preprocessing can effectively remove baseline and other background interference, separate overlapping peaks, and improve resolution and sensitivity. Baseline correction was used to adjust the spectral offset by adjusting the data to the minimum point in the data. De-trend is a transformation that seeks to remove nonlinear trends in spectroscopic data. OSC can be used as a transformation method for building PLS regression models from spectral data. It removes the extraneous variance from the x data, sometimes making the PLS model more accurate. Normalization is a family of transformations that are computed sample-wise. Its purpose is to “scale” samples to get all data on approximately the same scale. Through the establishment of the PLS model, the optimal spectral pretreatment method was obtained.

2.5. Model Development

Chemometrics is needed in qualitative and quantitative analyses. There are three commonly used modeling methods: partial least squares (PLS), principal component analysis (PCA), and artificial neural network (ANN). In the modeling method for near-infrared spectral analysis, the PLS method can effectively solve a large amount of near-infrared spectral information. The method of gradually adding new information can eliminate the influence caused by external noise to a certain extent, improve the data accuracy, and associate the independent variable with the dependent variable matrix to obtain the best model. The PLS regression method offers an effective combination of multiple linear regression and principal component regression. PLS analysis was developed to be a standard tool in chemometrics and is used widely in Vis/NIR spectral analysis. Based on the above characteristics, the present study uses the partial least squares method to model and analyze the carbon content of the sample.
The dataset was split into a calibration set and a validation set before model development using an SPXY algorithm (2:1). First, the data were modeled via PLS regression analysis, where the optimal latent variables were optimized with a five-fold cross-validation procedure. The PLSR model was tuned such that the maximum number of model components was set to 10. The model was then run and tested for each number of components from 1 to 10. The optimal number of components was chosen based on the lowest RMSECV via using cross-validation. Finally, the model was re-calibrated with the optimal number of components and validated, and the R2 and RMSE were calculated.

2.6. Model Evaluation

Evaluation of the model quality included the R square of calibration (R2c), the R square of prediction (R2p), the root means square error of calibration (RMSEC), the root mean square error of cross-validation (RMSECV), the root mean square error of prediction (RMSEP), and residual prediction deviation (RPD). The R square is used to describe the linear correlation between the predicted values and the measured values. The higher the R2p and the closer the R2c is to 1, the greater the correlation between the predicted value and actual value, and the stronger the robustness of the model. The RMSEC, RMSECV, and RMSEP were usf the calibration model. The loweed to evaluate the feasibility or the RMSEP is and the closer it is to the RMSEC, the stronger the predictive ability and the robustness of the calibration model are. RPD is a measure of a model’s ability to predict a constituent. Values between 2.0 and 2.5 indicate approximate quantitative predictions, while values between 2.5 and 3.0 and above 3.0 indicate predictions that can be considered good and excellent, respectively [35,52]. The computation equations for these criteria are as follows:
R 2 = 1 − ∑ i = 1 n ( y i − y i ^ ) 2 / ∑ i = 1 n ( y i − y ¯ ) 2
R M S E = ∑ i = 1 n ( y i − y i ^ ) 2 / n
R P D = S D / R M S E P
where y i represents the tracheid length value; y i ^ and y ¯ are the predicted value and the mean of y i , respectively; and n is the number of samples. When n is the number of samples in the calibration set, the coefficient of determination and the root mean square error are referred to as R2c and RMSEC, respectively. When n is the number of samples of the validation set, the coefficient of determination and the root mean square error are referred to as R2p and RMSEP, respectively. SD is the standard deviation.

2.7. Software

Statistical data analysis was completed in IBM SPSS Statistics 26.0 (IBM, Armonk, NY, USA). Transformation of the collected reflectance spectra into absorbance was performed in ViewSpecPro (ASD Inc. Boulder, CO, USA). All spectral preprocessing was performed iusingthe Unscrambler® X v10.4 software (CAMO Software Inc., Woodbridge, NJ, USA). The PLS modeling, SPXY algorithm, and figure were implemented in MATLAB R2016a (MathWorks, Natick, MA, USA).

3. Results and Discussion

3.1. Near-Infrared Spectral Features

Figure 2 shows that the six tree species had similar absorbance patterns, so a spectral was randomly selected for spectral analysis. The Vis-NIR spectra (350–2500 nm) of an increment core sample are shown in Figure 3. Prominent absorption peaks can be seen at 1171, 1418, 1752, 1882, 2050, and 2225 nm.
The peak at approximately 1171 nm was attributed to the second over-tone of symmetric and anti-symmetric C–H (–CH, –CH2, –CH3) stretch vibration. The peak at approximately 1418 nm indicates a combination of C–H stretching, vibrations, and bending vibrations. The above two peaks were also subject to the same analysis used in the experiment of Julia K. [40]. Here, peaks at 1752 nm correspond to the stretching vibrations of C–H in the first overtone. This peak is also in the 1726–1761 nm wavelength, as mentioned in [40]. The sharp peak at around 1882 nm was associated with the first overtone of O–H and C–H stretch vibrations. The peak at 2050 nm indicates a combination of N–H in-plane bending and C–H stretching from the protein compounds. The peak at around 2225 nm might result from a combination of C–H stretch vibrations and C=O stretch vibrations [42]. These peaks are mainly related to carbohydrates, lipids, and protein macromolecular organic matter [53,54]. The above characteristic peaks of element C suggest the potential use of NIR spectroscopy to predict the carbon content of tree species.

3.2. The Selection of Sample Sets

In the process of near-infrared analysis, it is generally considered that more than 50 samples can be used for modeling and analysis. A. Vergnoux et al. used only 55 soil samples to establish a near-infrared model for predicting the properties of soil organic carbon [55]. Hou R. et al. used 58 samples to establish a near-infrared model of barley protein, and the prediction results were good [37]. Marcelo A. and Helena P. established near-infrared models that used sample sizes of 53 and 60, respectively [38,41]. Thus, 96 increment core samples were used in this study to establish a near-infrared prediction model, and the sample size was reasonable.
Random sampling, Kennard stone, and the SPXY algorithm are the most common methods used to divide sample sets. However, the SPXY algorithm is more common than the first and second algorithms, which are based on the KS algorithm [56,57]. In this paper, the SPXY algorithm is used to divide the sample set by taking the measured carbon content as the Y variable and the spectral data as the X variable. Here, the distance between samples is calculated by using two variables simultaneously to ensure maximum representation of the sample distribution, effectively covering the multi-dimensional vector space, increasing the difference and representativeness between samples, and improving the stability of the model. Ninety-six samples were divided into 64 calibration sets and 32 validation sets using the SPXY algorithm according to a ratio of 2:1. The statistical results are shown in Table 2.
In Table 2, the carbon content of the calibration set samples covers the carbon content range of the validation set samples, and the coefficient of variation is less than 5%. Moreover, the standard deviation is very low, indicating that the data are relatively stable. The reasonable division of the sample set helped to establish a robust prediction model.

3.3. PLS Model Development

Due to the light scattering and different effective path lengths of solid samples, the NIR spectral data inevitably contained some unwanted variations or noise. In order to improve the model’s development and accuracy, it was necessary to perform data preprocessing correctly to reduce such unwanted variations [21,58]. In this study, we applied two important spectral pretreatment methods that are not commonly used. First, we chose the EMSC method rather than MSC. EMSC is an extension of conventional MSC, which is not limited to only removing multiplicative and additive effects from spectra. This extended method allows for better separation of physical light scattering effects from chemical light absorbance effects by including wavelength-dependent effects or a priori information in the modeling [59]. Second, we applied the OSC method, which can be used as a transformation method for building PLS regression models from spectral data. This method removes extraneous variance from the x data, sometimes making the PLS model more accurate. Because OSC depends upon Y-values, it requires a matrix with Y values, which must be accurate [44]. At the same time, we also compared several common spectral pretreatment methods. Spectra derivation was performed via Gap derivatives in Gap sizes of 27 points. Normalization was performed using range normalization. For this process, each row was divided by its range (max value-in value). The baseline was completed by a combination of linear baseline corrections (run first), followed by the baseline offset. De-trending is a type of transformation that seeks to remove nonlinear trends in spectroscopic data. For this method, we applied parameters in the polynomial order of 2 to the data.
Table 3 summarizes the model developments for PLS regression models under all the above spectral pretreatment methods for carbon content. Parameters including R2, RMSE, and RPD were used to evaluate model robustness. The results for the preprocessed spectra were improved compared to the results for the raw spectra. This result is the same as that of previous studies, in which the derivation [45,60,61], normalization, EMSC [59], and OSC [37] of the spectral data achieved better model performance than using raw spectra. Additionally, 1D offered better model performance than 2D and was much better than other methods, yielding an R2c of 0.92, R2p of 0.99, and RPD of 8.9. This result is superior to the results of the previous study by Steffen H. (R2c = 0.89, R2p = 0.79, and RPD = 2.17) [33]. It is generally agreed that a NIR model with an RPD value above 3.0 indicates an excellent prediction [28,53].
As a rule, after using different pretreatment spectra, the performance of the PLS model increased with an increase in the optimal principal-component numbers (as shown in the column of the optimal principal-component number in Table 3), except under baseline correction and 1D correction. For PLS regression models, it is vital to determine the number of the optimal principal component. Though an increase in the number of factors often leads to higher R2 values, the model is likely to have over-fitting issues and be unsuitable for predicting future unknown samples [62,63]. It can be seen from Table 3 that the optimal principal-component number of each pretreatment method is somewhat different. In this study, we modeled PLS regression analysis in which the optimal latent variables were optimized with a five-fold cross-validation procedure. The optimal number of components was chosen based on the lowest RMSECV via using cross-validation. The results are shown in Figure 4.
It can be seen from Figure 4 that almost all the curves have a trend of first decreasing and then increasing. Therefore, for each preprocessing method, we must find the optimal principal-component number with the lowest RMSECV value. The optimal principal-component number of the raw spectrum, OSC, normalization, EMSC, de-trend, 2D, 1D, and baseline correction is 2, 3, 5, 4, 3, 10, 8, and 4, respectively. We built a PLS regression model by preprocessing the data and the corresponding optimal principal-component number. The results showed that 1D and 2D offer lower RMSEC and RMSEP and higher R2c, R2p, and RPD values than other pretreatment methods. The raw and processed spectra were plotted in Figure 5.
The raw spectra and spectra processed by the seven methods are plotted in Figure 5. The 1D and 2D pretreatments spectra led to more evident and sharper peaks than the raw spectra and other methods at approximately 1400, 1800, and 2200 nm. The baseline drift can be eliminated, and the influence of background interference with NIR data can be reduced by using the derivation of preprocessed NIR data [61]. Xavier H. argued that first derivatives are used to remove baselines and second derivatives to removes slopes [64]. Tian W.F. also found that the characteristic spectral peak after 1D pretreatment was sharper than in the raw spectrum [62]. This result could explain why the derivation pretreatments of the spectra improved the model performance. Although the information on the near-infrared spectrum after 2D pretreatment was basically the same as after 1D pretreatment, the relative intensity of the near-infrared spectrum peak of 1D was higher than that of 2D, especially the peak intensity at 1882 nm. This result may reduce white noise, such as background noise, when constructing a near-infrared prediction model, thereby improving the model’s overall accuracy, which also explains why the modeling performance was higher when the 1D optimal principal-component number was 8 than when the 2D optimal principal-component number was 10.
Figure 6a,b shows that, in the prediction of the raw spectral model without pretreatment, in both the calibration and validation sets, the sample points are scattered and far away from the 1:1 line, and the fitted curve deviates from the 1:1 line. However, after 1D preprocessing, the prediction results clearly show that the data points—except for a point of obvious deviation—are all closer to the 1:1 line. Moreover, the fitting curve of the 1D pretreatment data is close to the 1:1 line, and the fitting curve of the validation set almost coincides with the 1:1 line. Comparing these two graphs, we can intuitively see that the spectral model performance after 1D pretreatment is much better than that of the raw spectrum.

3.4. Reduced Spectra Model

When the wavelength of the near-infrared spectrum is near 350 and 2500 nm, the near-infrared spectrum detector reaches the edge state, resulting in large noise, and the information intensity of the near-infrared spectrum becomes low throughout the whole spectrum region [62,65]. The high noise bands are mainly concentrated in the 350–400 and 2350–2500 nm bands [45], and obvious peaks of raw and processed spectra appear before 2350 nm. This section studies a near-infrared prediction model of carbon content in the 400–2350 nm band. As in the full-spectrum modeling process, seven different spectral preprocessing methods were performed on the reduced spectrum. The PLS modeling results of the reduced spectrum are shown in Table 4.
As shown in Table 4, the model with reduced spectra demonstrated better performance than the full-spectrum model for the raw spectrum. However, the R2c only improved by 7%. For the reduced spectra, except for OSC, which achieved better prediction performance than the raw data, the preprocessed spectral models were worse than the original spectral models. The R2c values of all models were lower than 0.7; only the R2p of OSC was higher when the raw spectrum model was used. Comparing Table 3 with Table 4 shows that the performance of the model after full-spectrum pretreatment was superior to that of all pretreated and non-pretreated reduced-spectrum models. These results illustrate that reduced spectra may not improve the prediction model’s performance in determining the carbon content of tree species. The reason for this result is that, although the noise is larger after 2350 nm, there are still C-related peaks from the C–H combination bands for lipid and protein absorption at 2350–2500 nm [53,66,67]. These C–H structures will affect the accurate determination of carbon content when using the NIR model. Some researchers noted that 2290–2400 nm wavelength regions are associated with organic matter [17,39]. Tian W.F.’s study highlighted that, for raw and 1D data, the reduced-spectrum (1333–2222 nm) model achieved better overall performance than the full-range (1000–2500 nm) model. However, for other types of preprocessing, the full-spectrum model was better than the corresponding reduced-spectrum model [62]. This result means that narrowing the spectrum will not necessarily improve regression performance.
In summary, taking six tree species as the research object, 96 sample sets were divided into 64 calibration sets and 32 validation sets using an SPXY algorithm with a ratio of 2:1. The NIR predicted carbon content model was established via PLS regression, and seven different spectral pretreatment methods were used to optimize the model. The performance of the full-spectrum and reduced-spectrum modeling was also compared. The results show that, for the full spectrum, the pretreatment methods can improve the accuracy of the model to different degrees. However, the reduced spectra could not improve the performance of the model in predicting the carbon content of tree species. The best performance ability of the model was 1D pretreatment of the full spectrum. After 1D pretreatment, the spectral model performance of each index was better than that of other methods: the R2c was 0.92, the R2p was 0.99, and the RMSE was 0.0056 and 0.0030. At the same time, RPD reached 8.9, which shows that the prediction performance of the model is excellent. Despite the six tree species and the limited samples available in our research, we achieved higher prediction accuracy than other studies. Moreover, this method can overcome the limitation of using only one tree species to build a model to predict unknown samples. The best prediction model and corresponding parameters are shown separately in Figure 7.

3.5. Comparison of Carbon Content of Tree Species

Here, we compared the carbon content of tree species predicted by the near-infrared best model with the global default value. In the calculation of forest carbon storage, the global default value of the carbon content of tree species is 0.5. The carbon content values of various tree species determined by the best spectral model are shown in Table 5.
Our results showed that the average carbon content ranges from 0.4352 to 0.4745, which was lower than the global default value (0.5). The mean carbon content across species was 0.4517, in agreement with other multi-species studies [10,11,12,14]. The results of one-way ANOVA showed that the average carbon content among species was significantly different (F = 24.07, p = 0.000). Compared with the global default value, the deviation of the carbon content of six tree species ranges from 5.4–14.9%.
While sampling, we also investigated the biomass of larch and birch natural mixed secondary forest in Daxing’anling. The results showed that the above-ground biomass of birch was 8.7 t ha−1, and larch was 105.7 t ha−1. The total above-ground biomass was 114.4 t ha−1. Using 0.5 as the carbon content, we overestimated the carbon density of the above-ground tree layer of the stand by 5 t ha−1 compared with the actual measurement. This result produced a 10% deviation in the estimation of the forest-tree carbon pool. If 0.45 is used as the carbon conversion coefficient, a deviation of 1% will occur, and the carbon density value is underestimated by 0.5 t ha−1. Although the difference of this result is small, it may have a great impact on other stands (such as a pure forest). Therefore, we believe that the measured carbon content of tree species is vital for the accurate estimate of forest carbon sink.

4. Conclusions

Overall, our study showed that NIR diffuse reflectance spectroscopy, combined with PLS regression, and selecting an appropriate spectral pretreatment method could be employed to detect and rapidly analyze carbon content in tree species. Compared to traditional carbon content measurement methods, this method can save time, labor, and money and realize non-destructive and in situ sensing, thereby providing a novel method for determining the carbon content in forest carbon sequestration measurements. In addition, this study confirmed that coupling Vis-NIR to a machine learning model offers a promising method for accelerating site investigations.

Author Contributions

Conceptualization, Y.L. and Y.M.; methodology, Y.M. and Y.Z.; software, Y.M. and J.Z.; validation, Y.Z. and C.L.; formal analysis, Y.Z.; investigation and sample collection, Y.M., Z.W. and C.W.; writing—original draft preparation, Y.M.; writing—review and editing, Y.L. and Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Fundamental Research Funds for the Central Universities, grant number 2572019AB17.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to it is being used to apply for project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Al-Ghussain, L. Global warming: Review on driving forces and mitigation. Environ. Prog. Sustain. Energy 2019, 38, 13–21. [Google Scholar] [CrossRef] [Green Version]
  2. Scheffer, M.; Brovkin, V.; Cox, P.M. Positive feedback between global warming and atmospheric CO2 concentration inferred from past climate change. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
  3. Wang, J.; Quan, Q.; Chen, W.; Tian, D.; Ciais, P.; Crowther, T.W.; Mack, M.C.; Poulter, B.; Tian, H.; Luo, Y.; et al. Increased CO2 emissions surpass reductions of non-CO2 emissions more under higher experimental warming in an alpine meadow. Sci. Total Environ. 2021, 769, 144559. [Google Scholar] [CrossRef]
  4. Węgiel, A.; Polowy, K. Aboveground Carbon Content and Storage in Mature Scots Pine Stands of Different Densities. Forests 2020, 11, 240. [Google Scholar] [CrossRef] [Green Version]
  5. Carvalhais, N.; Forkel, M.; Khomik, M.; Bellarby, J.; Jung, M.; Migliavacca, M.; Mu, M.; Saatchi, S.; Santoro, M.; Thurner, M.; et al. Global covariation of carbon turnover times with climate in terrestrial ecosystems. Nature 2014, 514, 213–217. [Google Scholar] [CrossRef] [Green Version]
  6. Hu, X.Y.; Duan, A.G. Advances in Carbon Reserve of Forest Ecosystems. For. Sci. Technol. 2020, 2, 3–6. [Google Scholar] [CrossRef]
  7. Vergara-Díaz, G.; Herrera-Machuca, M.Á. Estimation and spatial analysis of aerial biomass and carbon capture in native forests in the south of Chile: County of Valdivia. Rev. Chapingo Ser. Cienc. For. Ambiente 2020, 27, 53–71. [Google Scholar] [CrossRef]
  8. Solomon, N.; Birhane, E.; Tadesse, T.; Treydte, A.C.; Meles, K. Carbon stocks and sequestration potential of dry forests under community management in Tigray, Ethiopia. Ecol. Process. 2017, 6, 20. [Google Scholar] [CrossRef]
  9. Lu, J.; Feng, Z.; Zhu, Y. Estimation of Forest Biomass and Carbon Storage in China Based on Forest Resources Inventory Data. Forests 2019, 10, 650. [Google Scholar] [CrossRef] [Green Version]
  10. Yu, Y.; Fan, W.Y.; Li, M.Z. Forest carbon rates at different scales in Northeast China forest area. Chin. J. Appl. Ecol. 2012, 23, 341–346. [Google Scholar] [CrossRef]
  11. Li, B.; Fang, X.; Tian, D.L. Studies on carbon concentration of main forest vegetation tree species in Hunan province. J. Cent. South Univ. For. Technol. 2015, 1, 71–78. [Google Scholar] [CrossRef]
  12. Zhang, Q.; Wang, C.; Wang, X.; Quan, X. Carbon concentration variability of 10 Chinese temperate tree species. For. Ecol. Manag. 2009, 258, 722–727. [Google Scholar] [CrossRef]
  13. Dong, L.; Liu, Y.; Zhang, L.; Xie, L.; Li, F. Variation in Carbon Concentration and Allometric Equations for Estimating Tree Carbon Contents of 10 Broadleaf Species in Natural Forests in Northeast China. Forests 2019, 10, 928. [Google Scholar] [CrossRef] [Green Version]
  14. Pompa-García, M.; Sigala-Rodríguez, J.A.; Jurado, E.; Flores, J. Tissue carbon concentration of 175 Mexican forest species. Iforest—Biogeosci. For. 2017, 10, 754–758. [Google Scholar] [CrossRef] [Green Version]
  15. Gómez-García, E. Estimating the changes in tree carbon stocks in Galician forests (NW Spain) between 1972 and 2009. For. Ecol. Manag. 2020, 467, 118157. [Google Scholar] [CrossRef]
  16. Xu, Q.; Lin, L.; Xue, C.; Luo, Y.; Lei, Y. Component specific carbon content and storage of Cinnamomum camphora in Guangdong Province. J. Zhejiang AF Univ. 2019, 36, 70–79. [Google Scholar] [CrossRef]
  17. Sun, X.; Li, H.; Yi, Y.; Hua, H.; Guan, Y.; Chen, C. Rapid detection and quantification of adulteration in Chinese hawthorn fruits powder by near-infrared spectroscopy combined with chemometrics. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2021, 250, 119346. [Google Scholar] [CrossRef]
  18. Li, J.Y.; Chu, X.L.; Chen, P.; Tian, S.B. Application of Spectral Automatic Retrieval Algorithm on the Rapid Establishment of Gasoline Spectral Database. Acta Pet. Sin. 2017, 1, 131–137. [Google Scholar] [CrossRef]
  19. He, K.; Zhong, M.; Li, Z.; Liu, J. Near-infrared spectroscopy for the concurrent quality prediction and status monitoring of gasoline blending. Control. Eng. Pract. 2020, 101, 104478. [Google Scholar] [CrossRef]
  20. Mishra, P.; Herrmann, I.; Angileri, M. Improved prediction of potassium and nitrogen in dried bell pepper leaves with visible and near-infrared spectroscopy utilising wavelength selection techniques. Talanta 2021, 225, 121971. [Google Scholar] [CrossRef] [PubMed]
  21. Lin, Z.D.; Wang, Y.B.; Wang, R.J.; Wang, L.S.; Lu, C.P.; Zhang, Z.Y.; Song, L.T.; Liu, Y. Improvements of the Vis-NIRS Model in the Prediction of Soil Organic Matter Content Using Spectral Pretreatments, Sample Selection, and Wavelength Optimization. J. Appl. Spectrosc. 2017, 84, 529–534. [Google Scholar] [CrossRef]
  22. Shao, Y.; Jiang, L.; Zhou, H.; Pan, J.; He, Y. Identification of pesticide varieties by testing microalgae using Visible/Near Infrared Hyperspectral Imaging technology. Sci. Rep. 2016, 6, 24221. [Google Scholar] [CrossRef] [Green Version]
  23. Santos, I.A.; Conceicao, D.G.; Viana, M.B.; Silva, G.J.; Santos, L.S.; Ferrao, S.P.B. NIR and MIR spectroscopy for quick detection of the adulteration of cocoa content in chocolates. Food Chem. 2021, 349, 129095. [Google Scholar] [CrossRef] [PubMed]
  24. Jiang, Y.; Li, C.; Takeda, F. Nondestructive Detection and Quantification of Blueberry Bruising using Near-infrared (NIR) Hyperspectral Reflectance Imaging. Sci. Rep. 2016, 6, 35679. [Google Scholar] [CrossRef] [Green Version]
  25. Lakeh, M.A.; Karimvand, S.K.; Khoshayand, M.R.; Abdollahi, H. Analysis of residual moisture in a freeze-dried sample drug using a multivariate fitting regression model. Microchem. J. 2020, 154, 104516. [Google Scholar] [CrossRef]
  26. Ma, Y.; He, H.; Wu, J.; Wang, C.; Chao, K.; Huang, Q. Assessment of Polysaccharides from Mycelia of genus Ganoderma by Mid-Infrared and Near-Infrared Spectroscopy. Sci. Rep. 2018, 8, 10. [Google Scholar] [CrossRef] [PubMed]
  27. Hobley, E.; Steffens, M.; Bauke, S.L.; Kogel-Knabner, I. Hotspots of soil organic carbon storage revealed by laboratory hyperspectral imaging. Sci. Rep. 2018, 8, 13900. [Google Scholar] [CrossRef]
  28. Blaschek, M.; Roudier, P.; Poggio, M.; Hedley, C.B. Prediction of soil available water-holding capacity from visible near-infrared reflectance spectra. Sci. Rep. 2019, 9, 12833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  29. Amaral, E.A.; Dos Santos, L.M.; Hein, P.R.G.; Costa, E.V.S.; Rosado, S.C.S.; Trugilho, P.F. Evaluating basic density calibrations based on NIR spectra recorded on the three wood faces and subject to different mathematical treatments. N. Z. J. For. Sci. 2021, 51. [Google Scholar] [CrossRef]
  30. Pace, J.-H.C.; Latorraca, J.-V.D.F.; Hein, P.-R.G.; Carvalho, A.M.d.; Castro, J.P.; Silva, C.-E.S.d. Wood species identification from Atlantic forest by near infrared spectroscopy. For. Syst. 2019, 28, e015. [Google Scholar] [CrossRef]
  31. Li, Y.; Via, B.K.; Young, T.; Li, Y. Visible-Near Infrared Spectroscopy and Chemometric Methods for Wood Density Prediction and Origin/Species Identification. Forests 2019, 10, 1078. [Google Scholar] [CrossRef] [Green Version]
  32. Li, Y.; Via, B.K.; Cheng, Q. New Pretreatment Methods for Visible–Near-Infrared Calibration Modeling of Air-Dry Density of Ulmus pumila Wood. For. Prod. J. 2019, 69, 188–194. [Google Scholar] [CrossRef]
  33. Herrmann, S.; Bauhus, J. Nutrient retention and release in coarse woody debris of three important central European tree species and the use of NIRS to determine deadwood chemical properties. For. Ecosyst. 2018, 5, 22. [Google Scholar] [CrossRef] [Green Version]
  34. Elle, O.; Richter, R.; Vohland, M.; Weigelt, A. Fine root lignin content is well predictable with near-infrared spectroscopy. Sci. Rep. 2019, 9, 6396. [Google Scholar] [CrossRef] [PubMed]
  35. Li, X.; Sun, C.; Zhou, B.; He, Y. Determination of Hemicellulose, Cellulose and Lignin in Moso Bamboo by Near Infrared Spectroscopy. Sci. Rep. 2015, 5, 17210. [Google Scholar] [CrossRef] [PubMed]
  36. Murguzur, F.J.A.; Bison, M.; Smis, A.; Bohner, H.; Struyf, E.; Meire, P.; Brathen, K.A. Towards a global arctic-alpine model for Near-infrared reflectance spectroscopy (NIRS) predictions of foliar nitrogen, phosphorus and carbon content. Sci. Rep. 2019, 9, 8259. [Google Scholar] [CrossRef] [PubMed]
  37. Hou, R.; Ji, H.Y.; Zhang, D.L. Quantitative analysis of barley protein content based on OSC PLS algorithm. Spectrosc. Spectr. Anal. 2009, 7, 1840–1843. [Google Scholar] [CrossRef]
  38. Mareclo, A.M.; Cristiano, G.F. Determination of protection in field cru by specictroscopy NIR and PLS1. Sci. Technol. Food. Camp. 2005, 25, 25–31. [Google Scholar] [CrossRef] [Green Version]
  39. Kawamura, K.; Nishigaki, T.; Tsujimoto, Y.; Andriamananjara, A.; Rabenaribo, M.; Asai, H.; Rakotoson, T.; Razafimbelo, T. Exploring relevant wavelength regions for estimating soil total carbon contents of rice fields in Madagascar from Vis-NIR spectra with sequential application of backward interval PLS. Plant Prod. Sci. 2020, 24, 1–14. [Google Scholar] [CrossRef]
  40. Kuligowski, J.; Carrión, D.; Quintás, G.; Garrigues, S.; de la Guardia, M. Direct determination of polymerised triacylglycerides in deep-frying vegetable oil by near infrared spectroscopy using Partial Least Squares regression. Food Chem. 2012, 131, 353–359. [Google Scholar] [CrossRef]
  41. Pereira, H.; Santos, A.J.A.; Anjos, O. Fibre Morphological Characteristics of Kraft Pulps of Acacia melanoxylon Estimated by NIR-PLS-R Models. Materials 2016, 9, 8. [Google Scholar] [CrossRef] [Green Version]
  42. Costa, M.C.A.; Morgano, M.A.; Ferreira, M.M.C.; Milani, R.F. Analysis of bee pollen constituents from different Brazilian regions: Quantification by NIR spectroscopy and PLS regression. LWT 2017, 80, 76–83. [Google Scholar] [CrossRef]
  43. Pereira, E.V.d.S.; Fernandes, D.D.d.S.; de Araújo, M.C.U.; Diniz, P.H.G.D.; Maciel, M.I.S. Simultaneous determination of goat milk adulteration with cow milk and their fat and protein contents using NIR spectroscopy and PLS algorithms. LWT 2020, 127, 109427. [Google Scholar] [CrossRef]
  44. Biney, J.K.M.; Blöcher, J.R.; Borůvka, L.; Vašát, R. Does the limited use of orthogonal signal correction pre-treatment approach to improve the prediction accuracy of soil organic carbon need attention? Geoderma 2021, 388, 114945. [Google Scholar] [CrossRef]
  45. Yin, S.K.; Li, C.X.; Meng, Y.B. Near infrared spectral estimation and model optimization of Tilia tuan based on different pretreatments. J. Cent. South Univ. For. Technol. 2020, 40, 176–185. [Google Scholar] [CrossRef]
  46. Lu, B.; Wang, X.; Liu, N.; Hu, C.; Xu, H.; Wu, K.; Xiong, Z.; Tang, X. Quantitative NIR spectroscopy determination of coco-peat substrate moisture content: Effect of particle size and non-uniformity. Infrared Phys. Technol. 2020, 111, 103482. [Google Scholar] [CrossRef]
  47. Hao, Y.; Geng, P.; Wu, W.; Wen, Q.; Rao, M. Identification of Rice Varieties and Transgenic Characteristics Based on Near-Infrared Diffuse Reflectance Spectroscopy and Chemometrics. Molecules 2019, 24, 4568. [Google Scholar] [CrossRef] [Green Version]
  48. Liu, Y.; Liu, Y.; Chen, Y.; Zhang, Y.; Shi, T.; Wang, J.; Hong, Y.; Fei, T. The Influence of Spectral Pretreatment on the Selection of Representative Calibration Samples for Soil Organic Matter Estimation Using Vis-NIR Reflectance Spectroscopy. Remote Sens. 2019, 11, 450. [Google Scholar] [CrossRef] [Green Version]
  49. Wang, D.M.; Ji, J.M.; Gao, H.Z. The Effect of MSC Spectral Pretreatment Regions on Near Infrared Spectroscopy Calibration Results. Spectrosc. Spectr. Anal. 2014, 34, 2387–2390. [Google Scholar] [CrossRef]
  50. Taylor, A.R.; Wang, J.R.; Kurz, W.A. Effects of harvesting intensity on carbon stocks in eastern Canadian red spruce (Picea rubens) forests: An exploratory analysis using the CBM-CFS3 simulation model. For. Ecol. Manag. 2008, 255, 3632–3641. [Google Scholar] [CrossRef]
  51. Jiang, Z.H.; Huang, A.M.; Wang, B. Near Infrared Spectroscopy of Wood Sections and Rapid Density Prediction. Spectrosc. Spectr. Anal. 2006, 26, 1034–1037. [Google Scholar] [CrossRef]
  52. Zhu, H.; Chu, B.; Fan, Y.; Tao, X.; Yin, W.; He, Y. Hyperspectral Imaging for Predicting the Internal Quality of Kiwifruits Based on Variable Selection Algorithms and Chemometric Models. Sci. Rep. 2017, 7, 7845. [Google Scholar] [CrossRef] [Green Version]
  53. Lequeue, G.; Draye, X.; Baeten, V. Determination by near infrared microscopy of the nitrogen and carbon content of tomato (Solanum lycopersicum L.) leaf powder. Sci. Rep. 2016, 6, 33183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Krahmer, A.; Engel, A.; Kadow, D.; Ali, N.; Umaharan, P.; Kroh, L.W.; Schulz, H. Fast and neat--determination of biochemical quality parameters in cocoa using near infrared spectroscopy. Food Chem. 2015, 181, 152–159. [Google Scholar] [CrossRef] [PubMed]
  55. Vergnoux, A.; Dupuy, N.; Guiliano, M.; Vennetier, M.; Theraulaz, F.; Doumenq, P. Fire impact on forest soils evaluated using near-infrared spectroscopy and multivariate calibration. Talanta 2009, 80, 39–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Zhan, X.R.; Zhu, X.R.; Shi, X.Y. Determination of Hesperidin in Tangerine Leaf by Near-Infrared Spectroscopy with SPXY Algorithm for Sample Subset Partitioning and Monte Carlo Cross Validation. Spectrosc. Spectr. Anal. 2009, 29, 964–968. [Google Scholar] [CrossRef]
  57. Wang, S.F.; Han, P.; Cui, G.L.; Wang, D.; Liu, S.S.; Zhao, Y. The NIR Detection Research of Soluble Solid Content in Watermelon Based on SPXY Algorithm. Spectrosc. Spectr. Anal. 2019, 39, 738–742. [Google Scholar] [CrossRef]
  58. Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
  59. Liu, L.; Ye, X.P.; Saxton, A.M.; Womac, A. Pretreatment of near Infrared Spectral Data in Fast Biomass Analysis. J. Near Infrared Spectrosc. 2010, 18, 317–331. [Google Scholar] [CrossRef]
  60. Zhao, L.Z.; Guo, Y.; Dou, Y.; Wang, B.; Mi, H.; Ren, Y.L. Application of artificial neural networks to the nondestructive determination of ciprofloxacin hydrochloride in powder by short-wavelength NIR spectroscopy. J. Anal. Chem. 2007, 62, 1156–1162. [Google Scholar] [CrossRef]
  61. Xiong, Y.; Ohashi, S.; Nakano, K.; Jiang, W.; Takizawa, K.; Iijima, K.; Maniwara, P. Application of the radial basis function neural networks to improve the nondestructive Vis/NIR spectrophotometric analysis of potassium in fresh lettuces. J. Food Eng. 2021, 298, 110417. [Google Scholar] [CrossRef]
  62. Tian, W.; Chen, G.; Zhang, G.; Wang, D.; Tilley, M.; Li, Y. Rapid determination of total phenolic content of whole wheat flour using near-infrared spectroscopy and chemometrics. Food Chem. 2021, 344, 128633. [Google Scholar] [CrossRef]
  63. Faber, N.M.; Rajko, R. How to avoid over-fitting in multivariate calibration--the conventional validation approach and an alternative. Anal. Chim. Acta 2007, 595, 98–106. [Google Scholar] [CrossRef] [PubMed]
  64. Hadoux, X.; Gorretta, N.; Roger, J.-M.; Bendoula, R.; Rabatel, G. Comparison of the efficacy of spectral pre-treatments for wheat and weed discrimination in outdoor conditions. Comput. Electron. Agric. 2014, 108, 242–249. [Google Scholar] [CrossRef] [Green Version]
  65. Wang, X.S.; Qi, D.W.; Huang, A.M. Denoising of Near Infrared Spectroscopy in Wood Based on Wavelet TransformModulus Maximum. Sci. Silvae Sin. 2008, 10, 109–112. [Google Scholar] [CrossRef]
  66. Barbin, D.F.; Felicio, A.L.d.S.M.; Sun, D.-W.; Nixdorf, S.L.; Hirooka, E.Y. Application of infrared spectral techniques on quality and compositional attributes of coffee: An overview. Food Res. Int. 2014, 61, 23–32. [Google Scholar] [CrossRef] [Green Version]
  67. Westad, F.; Schmidt, A.; Kermit, M. Incorporating Chemical Band-Assignment in near Infrared Spectroscopy Regression Models. J. Near Infrared Spectrosc. 2008, 16, 265–273. [Google Scholar] [CrossRef]
Forests 12 01233 g001 550
Figure 1. Schematic diagram of the spectral collection of the increment core sample.
Figure 1. Schematic diagram of the spectral collection of the increment core sample.
Forests 12 01233 g001
Forests 12 01233 g002 550
Figure 2. Full-band near-infrared spectrum of 96 samples from six tree species.
Figure 2. Full-band near-infrared spectrum of 96 samples from six tree species.
Forests 12 01233 g002
Forests 12 01233 g003 550
Figure 3. The raw Vis-NIR spectra of the increment core sample.
Figure 3. The raw Vis-NIR spectra of the increment core sample.
Forests 12 01233 g003
Forests 12 01233 g004 550
Figure 4. Cross-validation results under different spectral preprocessing methods.
Figure 4. Cross-validation results under different spectral preprocessing methods.
Forests 12 01233 g004
Forests 12 01233 g005 550
Figure 5. Comparison of the raw and processed spectra in a wavelength range of 350–2500 nm.
Figure 5. Comparison of the raw and processed spectra in a wavelength range of 350–2500 nm.
Forests 12 01233 g005
Forests 12 01233 g006 550
Figure 6. PLS regression plot of reference values versus predicted values based on the raw original spectrum (a) and the 1D pretreatment spectrum (b).
Figure 6. PLS regression plot of reference values versus predicted values based on the raw original spectrum (a) and the 1D pretreatment spectrum (b).
Forests 12 01233 g006
Forests 12 01233 g007 550
Figure 7. The optimal prediction model of carbon content for tree species based on the full spectrum with 1D pretreatment.
Figure 7. The optimal prediction model of carbon content for tree species based on the full spectrum with 1D pretreatment.
Forests 12 01233 g007
Table
Table 1. Carbon content statistics of tree species.
Table 1. Carbon content statistics of tree species.
Tree Species NameNumber of SamplesMinimum
(g/g)		Maximum
(g/g)		Average Value
(g/g)		Standard Deviation
(g/g)
Betula platyphylla150.42000.45900.43660.0106
Abies fabri (Mast.) Craib150.45000.49500.47520.0126
Larix gmelinii150.43200.48000.45640.0155
Acer tegmentosum Maxim.150.41100.47400.43640.0154
Acer pictum Thunb. ex Murray160.41100.47100.43970.0178
Picea asperata Mast.200.44000.47800.46220.0104
total960.41100.49500.45150.0198
Table
Table 2. Statistical table for experimental sample validation set and calibration set carbon content.
Table 2. Statistical table for experimental sample validation set and calibration set carbon content.
Sample Set NameNumber of SamplesMinimum
(g/g)		Maximum
(g/g)		Average Value
(g/g)		Standard Deviation
(g/g)		Coefficient of Variation (%)
Calibration set640.41100.49520.45330.02034.48
Validation set320.42000.47700.44860.01773.95
Table
Table 3. PLS regression models for the carbon content of tree species based on different pretreatment.
Table 3. PLS regression models for the carbon content of tree species based on different pretreatment.
Spectral Pretreatment MethodCross-ValidationCalibration SetValidation Set
OPCRMSECVR2cRMSECR2pRMSEPRPD
Raw20.01540.650.01200.720.00911.9
EMSC40.01360.800.00900.950.00374.8
1D 80.01860.920.00560.990.00208.9
2D 100.02030.910.00590.980.00237.7
Baseline correction40.01580.730.01040.790.00812.2
de-trend30.01730.770.00960.860.00642.8
OSC30.01360.810.00880.950.00374.8
normalization50.01560.880.00710.960.00345.2
Table
Table 4. PLS regression models for the carbon content of tree species based on reduced spectra.
Table 4. PLS regression models for the carbon content of tree species based on reduced spectra.
Spectra and WavelengthSpectral Pretreatment MethodCross-ValidationCalibration SetValidation Set
OPCRMSECVR2cRMSECR2pRMSEP
Full Spectra
350–2500 nm		Raw20.01540.64670.01200.72420.0091
Reduced spectra
400–2350 nm		Raw70.01470.690.01110.870.0064
EMSC20.01610.460.01480.630.0105
1D20.01500.530.01390.700.0095
2D20.01500.590.01290.730.0091
Baseline correction30.01470.530.01380.650.0102
de-trend50.01570.640.01210.860.0065
OSC60.01420.690.01120.990.0001
normalization10.01480.500.01420.630.0109
Table
Table 5. Results of the carbon content determination by near infrared spectroscopy.
Table 5. Results of the carbon content determination by near infrared spectroscopy.
Tree Species NameNumber of SamplesMinimum
(g/g)		Maximum
(g/g)		Average Valu
(g/g)		Standard Deviation
(g/g)
Betula platyphylla150.41960.45980.4360 d0.0110
Abies fabri (Mast.) Craib150.45170.49850.4745 a0.0121
Larix gmelinii150.43690.48360.4559 bc0.0146
Acer tegmentosum Maxim.150.41170.46840.4352 d0.0148
Acer pictum Thunb. ex Murray160.41760.47630.4430 cd0.0144
Picea asperata Mast.200.44350.47880.4627 ab0.0095
total960.41170.49830.45170.0189
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Meng, Y.; Zhang, Y.; Li, C.; Zhao, J.; Wang, Z.; Wang, C.; Li, Y. Prediction of the Carbon Content of Six Tree Species from Visible-Near-Infrared Spectroscopy. Forests 2021, 12, 1233. https://doi.org/10.3390/f12091233

AMA Style

Meng Y, Zhang Y, Li C, Zhao J, Wang Z, Wang C, Li Y. Prediction of the Carbon Content of Six Tree Species from Visible-Near-Infrared Spectroscopy. Forests. 2021; 12(9):1233. https://doi.org/10.3390/f12091233

Chicago/Turabian Style

Meng, Yongbin, Yuanyuan Zhang, Chunxu Li, Jinghan Zhao, Zichun Wang, Chen Wang, and Yaoxiang Li. 2021. "Prediction of the Carbon Content of Six Tree Species from Visible-Near-Infrared Spectroscopy" Forests 12, no. 9: 1233. https://doi.org/10.3390/f12091233

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop