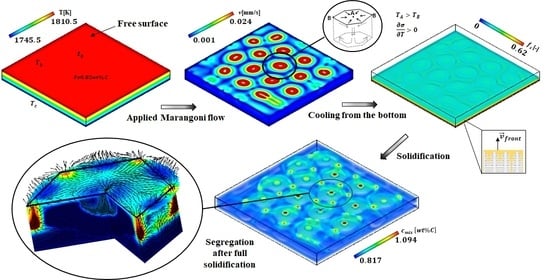
4.1. Effect of Liquid Depth and Thermal Gradient on Flow Pattern
The flow motion arises from the interplay between thermocapillary forces (induced by temperature-dependent surface tension) and buoyancy forces (driven by density variations due to temperature and concentration gradients). While the gravity vector acts from top to bottom, it is crucial to note that the primary driver of hydrodynamic instability is the Marangoni flow, which is formed at the free surface of the molten alloy, extending into the liquid depth. The Marangoni flow interacts with the natural convection, forming flow instability known as Rayleigh–Benard–Marangoni (RBM) instability. However, the solutal buoyancy is absent in
Section 4.1,
Section 4.2 and
Section 4.3, as the liquid prior to solidification preserves its initial concentration of 0.82wt%C. Three-dimensional simulations are developed to investigate the impact of the liquid depth (thickness) and the thermal gradient on the formation of Marangoni cells. Calculations were conducted on three cases with configurations given in
Table 2. All the studied flow situations are steady. However, the results have been evaluated using a transient solver.
The important flow parameters for RBM convection are the Marangoni and Rayleigh numbers, which are defined by Equations (11) and (12), as follows:
These two dimensionless numbers are important in RBM convection. Rachid Es Sakhy et al. [
7] analyzed the effect of the Marangoni number on flow for different Marangoni and Rayleigh numbers. They found that there are no hexagonally shaped convection cells formed for different Rayleigh numbers or
= 0. Nevertheless, as they set the Marangoni number to a high value (
= 2000), hexagonal cells were initiated and their number increased with an increasing Rayleigh number. In addition, the authors reported that the size and the number of hexagonal cells increase with an increase in the Marangoni number. However, the size and the number of the cells might also be changed, depending on the alloy type.
Figure 2 shows the velocity fields driven by RBM flow before solidification, where the Fe-0.82wt%C alloy is completely in a liquid state. The flow patterns were formed in hexagonal shapes due to the effect of the surface tension, which will be discussed in the next section. As has been found in numerous studies [
3,
7,
8,
9,
10], the formation of the hexagonal cells is mainly caused by the Marangoni flow, driven by the surface tension. However, in [
6,
7,
10], the authors reported that the size and the number of the hexagons is directly affected by the flow configuration and the aspect ratio. In order to examine the effect of the thermal gradient on flow configuration,
Figure 2b,c present two cases that have the same aspect ratio but different thermal gradient (DT = 65 K and 100 K, respectively). In these cases, the number of convective cells increased from 15 to 21 cells with the increase in the thermal gradient from 65 K to 100 K, which consequently increases the Marangoni number from
= 1186.8 to 1825.9. Thus, six more cells were added as a result of increasing the thermocapillary forces. However, the size of the formed cells decreased. In addition, the velocity value increased by about 3.5 times with the increase in the thermal gradient. The temperature coefficient of the surface tension was set to
N/m/K for the cases of low thickness (case b and c). To assess whether Marangoni values are within the magnitude of real steel melt, we would typically need experimental data. These data would include measurements or calculations related to the surface tension gradients and the associated Marangoni effect for molten steel. Due to the unavailability of these data, a parametric study was devoted to defining the corresponding value of this coefficient for a steel alloy. Based on the prescribed model, the value of
N/m/K can predict the effect of Marangoni flow on the formation of hexagonal patterns, which suggests this is the actual value of the Fe-0.82wt%C alloy. However, no validation has been made to confirm this judgement.
To examine the effect of the ingot thickness on the formation of the hexagonal cells, a larger geometry (8-fold) is presented in case (a) in
Figure 2. To keep the same Marangoni number (
= 1186.8), the value of
was reduced to
N/m/K (i.e., eight times less), while the thermal gradient remained unchanged (DT = 65 K). Based on the results of cases (a) and (c), with increasing the thickness to 8-fold, the number of the cells remained the same (15 cells), but their sizes increased dramatically with the increase in the thickness. According to these analyses, the general trend is that the number of Marangoni cells increases with an increasing Marangoni number. However, with increasing the thickness and keeping the same Marangoni, the number of cells remained the same, but the cell size increased. The flow strength was influenced by the characteristic length, which impacted the flow dynamics. Variations in the computing domain size led to changes in the corresponding Rayleigh and Marangoni numbers and then alterations in the flow characteristics. However, the case of e = 1.25 mm was investigated in this part (
Figure 2b,c) to understand the effect of the thermal gradient and the liquid depth on the formation of hexagonal patterns. However, for the next investigations, only the geometry with e = 10 mm (see
Figure 1) will be considered.
4.2. Effect of Surface Tension on the Flow Direction of Liquid
In this section, the flow pattern at the free surface before the solidification is investigated. Numerous mesh refinements were tested to examine the convergence of the model implemented and the minimal mesh size, which ensures the mesh’s independence of the given solution. The transport equations discussed in
Section 2 were solved using the pressure–velocity coupling SIMPLEC method within the finite volume method. To achieve convergence, up to eight iterations were performed for each 0.01 s timestep, to reduce the normalized residuals. The convergence criteria for the continuity equations, the momentum equations, and the solute equations were all set to 10
−3, while 10
−6 was chosen for the enthalpy equations (Equation (8)).
Figure 3 represents the velocity field (colored magnitude levels and black vectors) at the free surfaces (a) and (b) and on the cross-section presented in (c). The Marangoni effect is the mass transfer along an interface between two fluids due to the surface tension gradient (fluid from areas with low surface tension is transferred to areas with higher surface tension) [
23]. The Marangoni flow dominates the flow within the hexagonal cells (
Figure 3a). However, a downward flow is generated by RBM convection at the centers of the hexagonal cells, as shown in
Figure 3c. According to [
23], the sign of the temperature gradient of the surface tension (
) determines the direction of the fluid flow at the surface tension. A negative value of
indicates that the surface tension (
) reduces with increasing temperature, prompting a radial outward flow. Conversely, a positive surface tension gradient leads to a radial inward flow, as shown schematically in
Figure 3, which is the case in the present study.
4.3. Effect of Marangoni on Flow and Temperature Fields before Solidification
In this section, the effect of Marangoni convection on the flow and temperature distribution before solidification is presented. The resulting fields of the flow and temperature are shown in
Figure 4 in the left and right columns, respectively. The results at the horizontally cut plane of e = 0.4 mm from the bottom (
Figure 4 top) are also compared to those at the free surface (
Figure 4 bottom). As discussed earlier, the nonuniform temperature distribution exists along the free surface, which introduces a gradient in the surface tension. Despite the weak temperature difference between the hot and the cold regions along the free surface (~0.24 K), it was sufficient to direct the liquid metal from the cold towards the hot regions as a result of the positive temperature coefficient of the surface tension.
The movement of the flow along the free surface leads to the birth of fifteen convective hexagonal cells. Marangoni flow extended vertically along the liquid depth toward the bottom, producing regular, steady, hexagonal flow patterns that carry the hot fluid to the bottom, as shown in
Figure 4 at e = 0.4 mm. Indeed, the formed hexagonal patterns govern the whole domain and extend through the ingot depth, preserving the same position, as explained schematically in
Figure 1.
The temperature gradient at deeper planes (e = 0.4 mm) is weaker compared to the free top surface. However, the situation may change after solidification when the solute is rejected and the latent heat is released. Consequently, the velocity magnitude at the free top surface is higher than at the bottom region (about 27-fold); this is mainly caused by Marangoni flow, which is initiated at the free surface where there is a larger temperature gradient than at the bottom. The present analysis of the flow pattern and temperature distribution offers valuable insights into the flow behavior and the formation of the hexagonal patterns in the presence of a free surface. This analysis provides a preliminary estimate of the segregation pattern formed during solidification.
4.4. Marangoni Effect after Solidification
In this section, the solidification of the alloy is allowed and the impact of the flow pattern on the segregation structure is investigated. Thus, a convection heat transfer boundary condition with a heat transfer coefficient (HTC) of
was imposed along the free surface to govern the amount of heat transferred between the molten metal and the surroundings. A large heat transfer coefficient of
was also applied to the bottom surface to promote the growth of the columnar grains from the bottom upward. The formed solid fraction and the carbon concentration in the mixture (segregation pattern) when the solidification front reached the middle height of the ingot (at e = 5 mm) after t = 4863 s is shown in
Figure 5. The columnar dendrite trunks exhibit higher
close to the cold bottom of the ingot and decreases gradually towards the hot top (
Figure 5a). As expected, the solid fraction and the segregation structures formed at e = 5 mm above the ingot bottom have shapes analogous to the hexagonal convection cells formed at the free top surface. This behavior is mainly due to the Marangoni flow generated by surface tension, which is produced by the hexagonal structures throughout the liquid depth. However, a higher solute concentration was noted around the cells.
The solid front (at e = 5 mm from bottom) exhibited a concave shape, as evident from
Figure 5a, where periodic depressions in the solid front are observed. These depressions originate from the flow configuration generated by Marangoni flow, which drives the colder regions upwards. However, a downward hot flow persists in the center of the cells, maintaining these regions in liquid state, as depicted in
Figure 5c (blue region). The segregation map (
Figure 5b) gives the solute distribution, which varies in accordance with Equation (10). The region with higher solid fraction is characterized by a negative segregation pattern; this is because the mixture concentration is lower than the nominal value. Conversely, a positive segregation was developed around the cells as a result of the solute that was rejected from the solid to the liquid.
The solidification front takes about 4863 s (calculation time) or 128 s (solidification time) to reach the mid-height of the ingot. As the solidification front advanced towards the top, the thermal gradient gradually decreased, leading to an accelerated solidification rate.
Figure 6 presents top-view snapshots of the solid fraction (right) and the segregation map (left) at the final stages of solidification. The solidification front reached the top surface at t = 4890 s, confirming that the second half of the geometry solidified within only 27 s.
The columnar grains continue to solidify in a hexagonal cellular pattern, where the Marangoni flow is becoming more intense when the remaining liquid ahead of the solid front becomes shallower. However, the centers of the cells are still in a liquid state and characterized by higher temperature. It is noteworthy that the blue circular features of full liquid scattering at the periphery of the hexagonal cells are evident in
Figure 6 (right). These circles are in the form of tubes extending inside the mushy zone and are characterized by a high carbon content (
Figure 6 left). These tubes are called segregation channels, as shown in the zoomed-in view of a single hexagon (
Figure 7). They may also play a role in governing the hexagons’ location thanks to the arising flow presented by the black vectors inside the segregated channels shown in
Figure 7.
At the free surface, the upward stream inside the segregation channels flows toward the center of the hexagons (see
Figure 7). This liquid stream recirculates downwards through the mushy zone from the center of the hexagon at the free surface and then again towards the segregation channels. The flow patterns at the free surface and within the mushy zone exhibit similar characteristics to those observed in the liquid state prior to solidification, as discussed in
Section 4.2. This similarity arises from the influence of the positive coefficient of surface tension, which drives the flow’s recirculation. Therefore, the Marangoni flow induced by the surface tension gradient governs the configuration of segregation structures, particularly the location of the segregation channels.
At the end of solidification (
in the whole domain), the segregation pattern at three different cut planes in the solidification ingot was calculated; representations of the 0.1 mm, 5 mm, and 9 mm cut planes are presented in
Figure 8. It is obvious that the polygonised cells of the segregation patterns (very close to the hexagonal shape) are formed throughout the thickness of the ingot as a result of the Marangoni-induced flow. These segregation cells are characterized by higher carbon concentration at their edges compared to their centers. Also, the cells close to the bottom (0.1 mm plane) have thicker carbon-rich peripherals; however, the minimum and maximum segregation difference (ΔC) is weak. At the 5 mm cut plane, the regions with positive segregation become thinner, with a dramatic increase in segregation that reached 1.38wt%C. Close to the free surface (the 9 mm cut plane), very high positive segregation nodes are scattered around the hexagonal cells; their centers survived, even at the end of the solidification process. This is evidence for decaying segregated liquid recirculation, as explained in
Figure 7.
A quantitative analysis for the segregation that forms in different regions at the end of the solidification process was conducted, as shown in
Figure 9. The segregation differences (noted as “
”) at the 0.1, 2, 5, 7, and 9 mm cut planes were plotted (
Figure 9, left) in comparison with the segregation contours (
Figure 9, right). To facilitate the mapping between the left and right parts of
Figure 9, the cut planes shown on the right present the minimum and the maximum segregation levels of each plane. The results reveal a significant increase in segregation differences, from ΔC = 0.0007 for the 0.1 mm cut plane to
= 0.94-wt% for the 9 mm cut plane. A very weak segregation difference was observed close to the ingot’s bottom. This can be attributed to the weaker convection streams at the bottom compared to the top, as discussed previously in
Figure 4 (weaker Marangoni flow at the bottom). As the solidification starts from the bottom and advances towards the top, a small concentration gradient and, consequently, a weak segregation are formed at the horizontal plane (e = 0.1 mm). However, at the e = 2 mm horizontally cut plane, the segregation difference sharply increased to 0.029-wt% (about 41-fold) due to the substantial solute gradient. With the same tendency, the segregation difference further increased to 0.69-wt% at the mid-height (e = 5 mm), which is 23-fold greater than the segregation difference at e = 2 mm. The segregation difference continued to rise with increasing height of the ingot, reaching 0.73 and 0.94-wt% at e = 7 mm and e = 9 mm, respectively, as shown in
Figure 9.
The results presented in
Figure 9 provide compelling evidence that Marangoni flow directly impacted the morphology and the level of the segregation that has formed throughout the ingot. Interestingly, it was observed that an even weaker Marangoni flow (near the bottom region) was able to produce a hexagonal segregation pattern; however, this had a smaller
value. On the other hand, a stronger Marangoni flow, especially one that was closer to the free surface, was found to lead to more noticeable variations in the segregation.
The mechanical properties and the melting point of carbon steel are very sensitive to the steel’s carbon content. The carbon content within the solidification ingot was subjected to dramatic variations, as shown in
Figure 8; it may reach ~1.6wt%C at certain segregation nodes. This value is very close to the those in the cast iron composition range. In these areas, a large amount of the hard and brittle ‘cementite’ micro-constituent may be formed; in contrast, the other carbon-depleted areas contain a more ductile phase, ’ferrite’. On the other hand, the C-rich areas exhibit lower liquidus temperatures that may cause partial melting during the subsequent heat treatment processes of steel. Furthermore, a structural failure is expected to occur at the brittle nodes during the subsequent deformation processes. Therefore, the current analysis may assist researchers and industrial developers in building an understanding of the origins of segregation in depth; this is the key to avoiding or minimizing its formation. An area plot of the positive/negative segregation values in terms of normalized macro-segregation (
) [
24] within one convection cell is presented in
Figure 10, with the initial alloy composition being given by the value of 0; in contrast, positive and negative macro-segregations are being given by values above or below zero, respectively [
24]. The result presented in
Figure 10 (on the left) shows the contours of the mixture’s concentration. The carbon-rich areas are highlighted in red; meanwhile, the carbon-depleted regions are shown using blue.
Figure 10 (on the right) illustrates the normalized macro-segregation along the black dashed line drawn through the hexagonal cells, as per
Figure 10 (left). The results indicate a positive segregation at the edge of the hexagonal cell and a fluctuating negative segregation in the inner region of the hexagon.
In the future, the authors intend to extend the findings of the current study to research the effects of the temperature gradient throughout the height of the mold on the formed segregation. In attempts to eliminate the segregation driven by the Marangoni effect thus far, the authors are yet to explore the application of surface tension modification fluxes to the free surface and superimposing an electromagnetic stirring field.