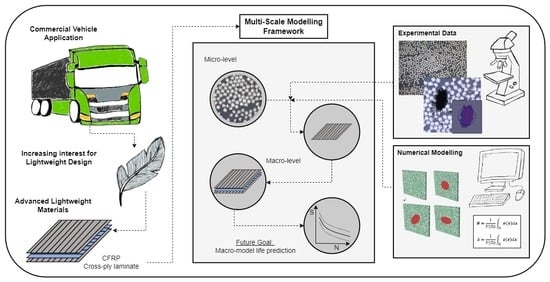
An Experimentally Based Micromechanical Framework Exploring Effects of Void Shape on Macromechanical Properties
Abstract
:1. Introduction
2. Methodology
2.1. Micrograph Data Extraction
2.1.1. Image Processing
2.1.2. Matrix, Fiber, and Void Data
2.1.3. Fiber Diameter and Nearest Neighbor Distributions
2.2. RVE Generation
2.2.1. Characterization of RVEs
- if: —remove the circumference within the void;
- if: —remove the circumference of the void within the observation area.
2.3. Numerical Analysis
2.3.1. FE Modeling
2.3.2. Periodic Boundary Conditions
2.3.3. Computational Homogenization
3. Case Study
3.1. Material System
3.2. Micrograph Data Extraction
3.2.1. Matrix, Fiber, and Void Data
3.2.2. Fiber Diameter and Nearest Neighbor Distributions
3.3. RVE Generation
Statistical Characterization of RVEs
3.4. FE Modeling
3.5. Results of the Case Study
3.5.1. Prediction of Macromechanical Properties
3.5.2. Verification with Static Testing
4. Discussion and Conclusions
4.1. RVE Generation
4.2. Implementation of Voids
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BDA | Blob Detection Algorithm |
| BEVs | Battery Electric Vehicles |
| BVP | Boundary Value Problem |
| CFRP | Carbon-Fiber-Reinforced Plastics |
| CLAHE | Contrast-Limited Adaptive Histogram Equalization |
| CLT | Classical Lamination Theory |
| CoG | Center of Gravity |
| CSR | Complete Spatial Randomness |
| DIC | Digital Image Correlation |
| FE | Finite Element |
| FEA | Finite-Element Analysis |
| LoG | Laplacian of Gaussian |
| MSM | Multi-Scale Modeling |
| NN | Nearest Neighbor |
| PBC | Periodic Boundary Condition |
| RVE | Representative Volume Element |
| SMC | Sheet Molding Compounds |
| SSE | Sum of Square Error |
| UD | Unidirectional |
| UTS | Ultimate Tensile Strength |
Appendix A. Computational Homogenization
References
- Czerwinski, F. Current Trends in Automotive Lightweighting Strategies and Materials. Materials 2021, 14, 6631. [Google Scholar] [CrossRef]
- Talreja, R. Multiscale Modeling. Compr. Compos. Mater. II 2018, 2, 148–166. [Google Scholar] [CrossRef]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Luger, M.; Traxl, R.; Hofer, U.; Hirzinger, B.; Lackner, R. RUC-based multi-scale model for braid-reinforced polymers: Application to coil springs. Compos. Part B 2018, 155, 431–443. [Google Scholar] [CrossRef]
- Montesano, J.; Chu, H.; Singh, C.V. Development of a physics-based multi-scale progressive damage model for assessing the durability of wind turbine blades. Compos. Struct. 2016, 141, 50–62. [Google Scholar] [CrossRef]
- Llorca, J.; González, C.; Molina-Aldareguía, J.M.; Segurado, J.; Seltzer, R.; Sket, F.; Rodríguez, M.; Sádaba, S.; Muñoz, R.; Canal, L.P. Multiscale Modeling of Composite Materials: A Roadmap Towards Virtual Testing. Adv. Mater. 2011, 23, 5130–5147. [Google Scholar] [CrossRef]
- Pavasson, J.; Ljung, A.L.; Karlberg, M.; Larsson, I.A.S.; Johansson, S.; Lundström, T.S. Challenges and opportunities within simulation-driven functional product development and operation. In Proceedings of the 3rd International Conference on Through-Life Engineering Services, Cranfield, UK, 4–5 November 2014; pp. 169–174. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; Fish, J. Toward realization of computational homogenization in practice. Int. J. Numer. Methods Eng. 2008, 73, 361–380. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. A virtual framework for prediction of full-field elastic response of unidirectional composites. Comput. Mater. Sci. 2013, 70, 82–99. [Google Scholar] [CrossRef]
- Sun, Q.; Meng, G.Z.Z.; Jain, M.; Su, X. An integrated computational materials engineering framework to analyze the failure behaviors of carbon fiber reinforced polymer composites for lightweight vehicle applications. Compos. Sci. Technol. 2021, 202, 108560. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Gorbatikh, L.; Verpoest, I.; Lomov, S.V. Voids in fiber-reinforced polymer composites: A review on their formation, characteristics, and effects on mechanical performance. J. Compos. Mater. 2018, 53, 1579–1669. [Google Scholar] [CrossRef]
- Talreja, R. Defect damage mechanics: Broader strategy for performance evaluation of composites. Plast. Rubber Compos. 2009, 38, 49–54. [Google Scholar] [CrossRef]
- Hyde, A.; He, J.; Cui, X.; Lua, J.; Liu, L. Effects of microvoids on strength of unidirectional fiber-reinforced composite materials. Compos. Part B 2020, 187, 107844. [Google Scholar] [CrossRef]
- Dong, C. Effects of Process-Induced Voids on the Properties of Fibre Reinforced Composites. J. Mater. Sci. Technol. 2016, 32, 597–604. [Google Scholar] [CrossRef] [Green Version]
- Maragoni, L.; Carraro, P.; Quaresimin, M. Prediction of fatigue life to crack initiation in unidirectional plies containing voids. Compos. Part A 2019, 127. [Google Scholar] [CrossRef]
- Huang, H.; Talreja, R. Effects of void geometry on elastic properties of unidirectional fiber reinforced composites. Compos. Sci. Technol. 2005, 65, 1964–1981. [Google Scholar] [CrossRef]
- Becker, F.; Hopmann, C. Stiffness Estimates for Composites with Elliptic Cylindrical Voids. Materials 2020, 13, 1354. [Google Scholar] [CrossRef] [Green Version]
- Hsu, D.K.; Uhl, K.M. A morphological study of porosity defects in graphite-epoxy composites. Rev. Prog. Quant. Nondestruct. Eval. 1986, 6B, 1175–1184. [Google Scholar] [CrossRef] [Green Version]
- Kouznetsova, V.; Brekelmans, W.A.M.; Baaijens, F.P.T. An approach to micro-macro modeling of heterogeneous materials. Comput. Mech. 2001, 27, 37–48. [Google Scholar] [CrossRef]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Vaughan, T.; McCarthy, C. A combined experimental-numerical approach for generating statistically equivalent fibre distributions for high strength laminated composite materials. Compos. Sci. Technol. 2010, 70, 291–297. [Google Scholar] [CrossRef] [Green Version]
- Cilley, E.; Roylance, D.; Schneider, N. Methods of Fiber and Void Measurement in Graphite/Epoxy Composites; Special Technical Publication 546; American Society for Testing and Materials: West Conshohocken, PA, USA, 1974. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobbs J. Softw. Tools 2000. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Python 3.7 Scikit-Learn Package. K-Means Clustering. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html (accessed on 30 August 2021).
- Fanni, S. Void Content Computation Using Optical Microscopy for Carbon Fiber Composites. Master’s Thesis, KTH, School of Engineering Sciences and Engineering Mechanics, Stockholm, Sweden, 2020. Project TRITA-SCI-GRU. p. 347. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Python 3.7 Scikit-Image Package. Blob Detection. Available online: https://scikit-image.org/docs/dev/api/skimage.feature.html#skimage.feature.blob_log (accessed on 30 August 2021).
- Python 3.7 Scikit-Learn Package. Nearest Neighbor Algorithms. Available online: https://scikit-learn.org/stable/modules/neighbors.html#nearest-neighbor-algorithms (accessed on 30 August 2021).
- Python 3.7 Scipy.Stats Package. Statistical Functions. Available online: https://docs.scipy.org/doc/scipy/reference/stats.html (accessed on 30 August 2021).
- Trias, D.; Costa, J.; Mayugo, J.; Hurtado, J. Random models versus periodic models for fibre reinforced composites. Comput. Mater. Sci. 2006, 38, 316–324. [Google Scholar] [CrossRef]
- Swaminathan, S.; Ghosh, S.; Pagano, N. Statistically equivalent representative volume elements for unidirectional composite microstructures: Part I—Without damage. J. Compos. Mater. 2006, 40, 583–604. [Google Scholar] [CrossRef]
- Maragoni, L.; Carraro, P.; Quaresimin, M. Development, validation and analysis of an efficient micro-scale representative volume element for unidirectional composites. Compos. Part A 2018, 110, 268–283. [Google Scholar] [CrossRef]
- Elnekhaily, S.A.; Talreja, R. Damage initiation in unidirectional fiber composites with different degrees of nonuniform fiber distribution. Compos. Sci. Technol. 2018, 155, 22–32. [Google Scholar] [CrossRef]
- Iizukaa, K.; Ueda, M.; Takahashi, T.; Yoshimura, A.; Nakayama, M. Development of a three-dimensional finite element model for a unidirectional carbon fiber reinforced plastic based on X-ray computed tomography images and the numerical simulation on compression. Adv. Compos. Mater. 2019, 28, 73–85. [Google Scholar] [CrossRef]
- Yokozeki, T.; Takemura, H.; Aoki, T. Numerical analysis on the flexural strength of unidirectional CFRTP composites with in-plane fiber bundle waviness. Adv. Compos. Mater. 2020, 29, 89–100. [Google Scholar] [CrossRef]
- Carraro, P.; Maragoni, L.; Quaresimin, M. Influence of manufacturing induced defects on damage initiation and propagation in carbon/epoxy NCF laminates. Adv. Manuf. Polym. Compos. Sci. 2015, 1, 44–53. [Google Scholar] [CrossRef]
- Pyrz, R. Quantitative description of the microstructure of composites. Part I: Morphology of unidirectional composite systems. Compos. Sci. Technol. 1994, 50, 197–208. [Google Scholar] [CrossRef]
- Pyrz, R. Correlation of microstructure variability and local stress field in two-phase materials. Mater. Sci. Eng. 1994, A177, 253–259. [Google Scholar] [CrossRef]
- Ripley, B.D. Modelling Spatial Patterns. J. R. Stat. Soc. Ser. B 1977, 39, 172–212. [Google Scholar] [CrossRef]
- Groen, D.; Knap, J.; Neumann, P.; Suleimenova, D.; Veen, L.; Leiter, K. Mastering the scales: A survey on the benefits of multiscale computing software. Philos. Trans. A 2019, 377, 20180147. [Google Scholar] [CrossRef]
- Tchalla, A.; Belouettar, S.; Makradi, A.; Zahrouni, H. An ABAQUS toolbox for multiscale finite element computation. Compos. Part B 2013, 52, 323–333. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for peroidic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef] [Green Version]
- Riaño, L.; Joliff, Y. An ABAQUS plug-in for the geometry generation of Representative Volume Elements with randomly distributed fibers and interphases. Compos. Struct. 2019, 209, 644–651. [Google Scholar] [CrossRef]
- Goodsell, J.; Spoonire, R.A. Micromechanical finite element modeling of fiber epoxy composites containing void defects part 1: Stiffness analysis. In Proceedings of the 19th AIAA Non-Deterministic Approaches Conference, AIAA SciTech Forum, Grapevine, TX, USA, 9–13 January 2017; p. 0820. [Google Scholar] [CrossRef]
- Trias, D.; Costa, J.; Turon, A.; Hurtado, J. Determination of the critical size of a statistical representative volume element (SRVE) for carbon reinforced polymers. Acta Mater. 2006, 54, 3471–3484. [Google Scholar] [CrossRef]
- Garoz, D.; Gilabert, F.A.; Sevenois, R.D.B.; Spronk, S.W.F.; Paepegem, W.V. Consistent application of periodic boundary conditions in implicit and explicit finite element simulations of damage in composites. Compos. Part B 2019, 168, 254–266. [Google Scholar] [CrossRef]
- Kouznetsova, V. Computational Homogenization for the Multi-Scale Analysis of Multi-Phase Materials; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, Y.; Ellyin, F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]
- Toray, I.I. Carbon Fiber Composite Materials. Available online: https://www.toray.com/global/ (accessed on 19 March 2021).
- Gil, R.G. Forming and Consolidation of Textile Composites. Ph.D. Thesis, School of Mechanical, Materials, Manufacturing Engineering and Management, University of Nottingham, Nottingham, UK, 2003. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 2019; Dassault Systèmes Simulia Corp: Mayfield Heights, OH, USA, 2019. [Google Scholar]
- BETA. ANSA Version 20.0.x User Guide; BETA CAE Systems: Root, Switzerland, 2019. [Google Scholar]
- Nagai, H.; Fujita, K.; Urabe, K.; Iwashita, N. FEM analysis of flexural modulus of carbon fiber monofilament considering anisotropy. Adv. Compos. Mater. 2022, 31, 137–150. [Google Scholar] [CrossRef]
- Balasubramani, N.K.; Zhang, B.; Chowdhury, N.T.; Mukkavilli, A.; Suter, M.; Pearce, G.M. Micro-mechanical analysis on random RVE size and shape in multiscale finite element modelling of unidirectional FRP composites. Compos. Struct. 2022, 282, 115801. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM Standard D3039/D3039M-17; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Eliasson, S.; Wanner, S.; Barsoum, Z.; Wennhage, P. Development of fatigue testing Procedure for unidirectional carbon fiber composites. Procedia Struct. Integr. 2019, 19, 81–89. [Google Scholar] [CrossRef]
- Purslow, D. On the optical assessment of the void content in composite materials. Composites 1984, 15, 207–210. [Google Scholar] [CrossRef] [Green Version]


















| Magnification | Avg. (-) | Avg. (-) | Avg. (-) |
|---|---|---|---|
| 5 | N/A | N/A | 0.0062 |
| 20 | 0.5808 | 0.4192 | N/A |
| 50 | 0.5963 | 0.4037 | N/A |
| (-) | (m) | Area (m) | (-) | (-) (w.o. Void) |
|---|---|---|---|---|
| 0.2498 | 112.8 | 10,000 | 0.4341 | 0.5787 |
| 0.2003 | 101.0 | 8000 | 0.4757 | 0.5949 |
| 0.1500 | 87.4 | 6000 | 0.4943 | 0.5815 |
| 0.1001 | 71.4 | 4000 | 0.5300 | 0.5890 |
| 0.0499 | 50.4 | 2000 | 0.5656 | 0.5953 |
| 0.0249 | 35.6 | 1000 | 0.5751 | 0.5898 |
| 0.0125 | 25.2 | 500 | 0.5852 | 0.5925 |
| 0.0062 | 17.8 | 250 | 0.5880 | 0.5917 |
| 0.0025 | 11.2 | 100 | 0.5958 | 0.5972 |
| [-] | Major Axis, a (m) | Minor Axis, b (m) | Area (m) | (-) | (-) (w.o. Void) |
|---|---|---|---|---|---|
| 0.2503 | 73.6 | 43.3 | 10,000 | 0.4420 | 0.5896 |
| 0.2000 | 65.8 | 38.7 | 8000 | 0.4675 | 0.5844 |
| 0.1500 | 57.0 | 33.5 | 6000 | 0.4945 | 0.5818 |
| 0.1001 | 46.5 | 27.4 | 4000 | 0.5273 | 0.5859 |
| 0.0501 | 32.9 | 19.4 | 2000 | 0.5657 | 0.5956 |
| 0.0251 | 23.3 | 13.7 | 1000 | 0.5767 | 0.5915 |
| 0.0125 | 16.4 | 9.7 | 500 | 0.5870 | 0.5945 |
| 0.0062 | 11.6 | 6.8 | 250 | 0.5912 | 0.5949 |
| 0.0025 | 7.4 | 4.3 | 100 | 0.5938 | 0.5953 |
| (-) | Major Axis, a (m) | Minor Axis, b (m) | Area (m) | (-) | (-) (w.o. Void) |
|---|---|---|---|---|---|
| 0.2503 | 73.6 | 43.3 | 10,000 | 0.4383 | 0.5847 |
| 0.2000 | 65.8 | 38.7 | 8000 | 0.4583 | 0.5728 |
| 0.1500 | 57.0 | 33.5 | 6000 | 0.4899 | 0.5763 |
| 0.1001 | 46.5 | 27.4 | 4000 | 0.5305 | 0.5895 |
| 0.0501 | 32.9 | 19.4 | 2000 | 0.5692 | 0.5993 |
| 0.0251 | 23.3 | 13.7 | 1000 | 0.5850 | 0.6000 |
| 0.0125 | 16.4 | 9.7 | 500 | 0.5830 | 0.5903 |
| 0.0062 | 11.6 | 6.8 | 250 | 0.5959 | 0.5996 |
| 0.0025 | 7.4 | 4.3 | 100 | 0.5868 | 0.5882 |
| Property | Avg. Value |
|---|---|
| 136,395 MPa | |
| 7900 MPa | |
| 7904 MPa | |
| 4235 MPa | |
| 2908 MPa | |
| 4244 MPa | |
| 0.22 | |
| 0.01 | |
| 0.22 | |
| 0.01 | |
| 0.36 | |
| 0.36 |
| UTS (MPa) | Stiffness (MPa) |
|---|---|
| 1377 | 68,519 |
| 1268 | 67,368 |
| (-) | Circular Void | Circular Void | Elliptical Void | Elliptical Void | Elliptical Void | Elliptical Void |
|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | |
| 0.25 | 52,352 | 2485 | 52,677 | 1956 | 52,687 | 2374 |
| 0.20 | 57,087 | 2825 | 55,909 | 2339 | 55,490 | 2649 |
| 0.15 | 59,858 | 3085 | 59,624 | 2768 | 59,495 | 3007 |
| 0.10 | 64,753 | 3467 | 63,790 | 3224 | 64,265 | 3403 |
| 0.05 | 68,734 | 3835 | 68,528 | 3733 | 69,320 | 3850 |
| 0.025 | 70,567 | 4078 | 69,933 | 3948 | 71,309 | 4081 |
| 0.0125 | 71,573 | 4149 | 71,585 | 4118 | 71,200 | 4119 |
| 0.006 | 71,806 | 4191 | 72,287 | 4217 | 72,419 | 4236 |
| 0.0025 | 72,580 | 4239 | 72,960 | 4294 | 71,912 | 4207 |
| 0 | 72,308 | 4235 | 72,308 | 4235 | 72,308 | 4235 |
| Property | RVE 200 m No Void (Baseline) | RVE 200 m Circ. Void | RVE 400 m Circ. Void | RVE 200 m Ellip. Void | RVE 400 m Ellip. Void |
|---|---|---|---|---|---|
| (-) | 0 | 0.0062 | 0.0062 | 0.0062 | 0.0062 |
| Void size | - | = 17.8 m | = 35.6 m | a = 11.6 m b = 6.8 m | a = 23.2 m b = 13.6 m |
| (-) | 0.5902 | 0.5880 (incl. void) | 0.5965 (incl. void) | 0.5912 (incl. void) | 0.5920 (incl. void) |
| (MPa) | 136,395 | −0.61% | +0.83% | +0.10% | −0.48% |
| (MPa) | 7900 | −2.11% | −1.09% | −2.24% | −2.59% |
| (MPa) | 7904 | −2.02% | −1.23% | −1.13% | −1.35% |
| (MPa) | 4235 | −1.04% | 0.50% | −0.43% | −1.02% |
| (MPa) | 2908 | −1.65% | −0.89% | −1.51% | −1.62% |
| (MPa) | 4244 | −1.32% | +0.02% | −0.57% | −0.94% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eliasson, S.; Karlsson Hagnell, M.; Wennhage, P.; Barsoum, Z. An Experimentally Based Micromechanical Framework Exploring Effects of Void Shape on Macromechanical Properties. Materials 2022, 15, 4361. https://doi.org/10.3390/ma15124361
Eliasson S, Karlsson Hagnell M, Wennhage P, Barsoum Z. An Experimentally Based Micromechanical Framework Exploring Effects of Void Shape on Macromechanical Properties. Materials. 2022; 15(12):4361. https://doi.org/10.3390/ma15124361
Chicago/Turabian StyleEliasson, Sara, Mathilda Karlsson Hagnell, Per Wennhage, and Zuheir Barsoum. 2022. "An Experimentally Based Micromechanical Framework Exploring Effects of Void Shape on Macromechanical Properties" Materials 15, no. 12: 4361. https://doi.org/10.3390/ma15124361