In this section, the jets’ flow dynamics and velocity profiles obtained for the three plate configurations are analyzed and discussed. The heat transfer measurements are also presented and support the main conclusions obtained from the PIV measurements.
4.1. Multiple Jet Impingement Flow Dynamics
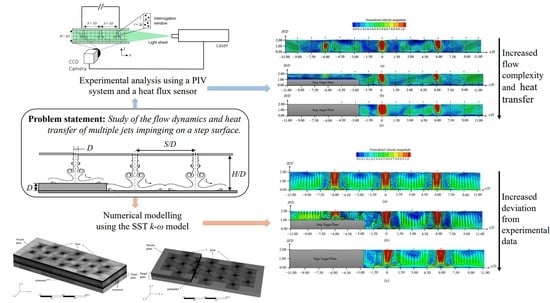
The averaged velocity field of multiple jets impinging on target plates with different configurations was obtained from PIV measurements, and the results are presented in
Figure 8. As previously mentioned, the row illuminated by the laser sheet contained the central jet and two adjacent jets, one on each side. However, the effect of the jets located at the front and back rows also had to be quantified due to the staggered configuration. In summary, the multiple jet flow analysis consisted of seven jets. Even if the measuring zone was totally open, the effect of the outlets on the impingement could only be considered on the right and left end side of the impingement plate since a total of nine rows (four on each side of the central row) were considered.
Starting with an overall analysis of the multiple jets’ flow dynamics depicted in
Figure 8, it was observed that the air flowed through the circular nozzles at a maximum velocity and started to mix with the surrounding air, entraining mass, momentum, and energy [
52]. This is known as the free jet region. From the mixing between the jet flow and the ambient air, a shear layer was generated leading to high lateral velocity gradients. As mentioned by [
53], jet impingements characterized by 0.5 <
H/
D < 5 are within the length of the potential core. This means that no decaying or fully developed regions were expected to be identified. As the jets approached the wall, the axial velocity decreased and was transformed into an accelerated horizontal component [
54]. This was identified as the stagnation region, which was characterized by a higher static pressure and a thin boundary layer [
55]. The development of the flow over the target plate induced a wall jet region, in which the flow velocity was accelerated along the plate from zero to a maximum at a specific distance from the stagnation point. The jets’ flow was divided into two streams moving in opposite directions, being characterized by a growing boundary layer [
56]. Considering this jet flow structure, higher heat transfer coefficients were expected to be recorded in the vicinity of the stagnation region, but a portion of the wall jet region significantly contributed to the heat exchange [
57]. However, as presented in
Figure 8, the jets’ flow complexity not only was increased by the jets’ interactions upstream and downstream of the impingement but also was increased by the non-flat plate.
Considering that the ratio
H/
D was small, a high velocity magnitude was identified from the nozzle exit to the target surface. Observing in detail the central jet, results show that the wall jet developed through the surface until it collided with the wall jet of adjacent jets located in the back and front rows. These interactions induced a fountain flow at
x/
D ≈ ±3 and recirculation regions, identified by Caliskan et al. [
58] as primary vortices. The magnitude and structure of these vortices, located on both sides of the central jet axis, seemed to be symmetric in the flat plate case (
Figure 8a). As the flow went through the outlets, an increase in the velocity magnitude was observed in direction of the adjacent jets, located at
x/
D equal to ±6. The interactions between the wall jets induced by the central jet and the adjacent jets located at the front and back rows led to a deflection of the adjacent jets flow located at
x/
D = ±6. This deflection was mainly due to the development of primary vortices generated at the right end side of the left jet and at the left end side of the right jet, which resulted from wall-jets development and jet-induced crossflow generated by the upstream jets. As mentioned by [
55], the self-induced crossflow causes an asymmetric jet flow field, disturbs other wall jets, moves the stagnation points, and develops thicker boundary layers, reducing the average heat transfer rates. This behavior was clearly observed in the three cases presented in
Figure 8. Thus, a reduction in the stagnation region of adjacent jets located at
x/
D = ±6 was verified and a weaker local heat transfer was expected in this region. The second increase in velocity magnitude was observed at
x/
D ≈ ±9, which represented the position of adjacent jets located at the front and back rows. The increased flow velocity was clear near the outlets, showing the magnitude of the crossflow generated by the upstream jets flow.
Regarding the non-flat plate case, the jet flow dynamics were slightly different. As identified in
Figure 8b, the wall jet development induced by the central jet was blocked by the step, inducing a flow reversal. In addition, the step deflected the flow from the adjacent jets located just above the step. The combination of these two effects increased the flow turbulence and affected the central jet flow. The vortex-induced in the left-hand side of the central jet deflected the central jet flow, and the stagnation point was moved to the right side. Even if the primary structure of the central jet was affected, the vortex promoted the mixing, which may have enhanced the heat transfer at the stagnation point [
54]. Comparing the two-step configurations, with 1
D (
Figure 8b) and 2
D (
Figure 8c) heights, the average velocity field shows that the 2
D step blocked the flow generated by the jets located immediately above step, while in the 1
D case, the small gap enabled the development of a short jet over the surface, ensuring its cooling. In that sense, higher velocities were induced in the vicinity of the 2
D step, increasing the overall turbulence of the flow. The deflection of the central jet was weaker when compared with the 1
D step. Therefore, there was no motion of the stagnation point. It was expected that this increased turbulence would enhance the heat transfer rates compared with the flat plate and the 1
D step.
As in the flat plate case, an increased velocity between the central jet and those adjacent, promoted by the jets located at the front and back rows, was identified. As the wall jet induced by the central jet went through the outlet, colliding with the wall jets from the adjacent jets, the deflection of the adjacent jets located at x/D = −6 was observed. This led to a decrease in the impingement area, and a reduced local heat transfer was expected in this region.
Beyond the influence of the target plate configuration, the PIV measurements show that the confined space played an important role in the velocity magnitude. Since the jets’ flow had a reduced space in which to develop, an increase in the flow vorticity was observed. The increase in velocity led to an overall increase in the flow turbulence. Including a step over the target plate, this space became even smaller, which induced a stronger mixing between the multiple jets flow and the surrounding air. In that sense, higher heat transfer rates were expected over a non-flat plate with the configurations presented in this study.
4.2. Velocity Profile over the Target Plate
The velocity profile over the target plate is depicted in
Figure 9 for the three plate configurations. To conduct the analysis, the average velocity magnitude was normalized by the maximum velocity (
max), as well as the distance from the central jet axis (
x/
D).
An overall view of the velocity field over the target plate, depicted in
Figure 9, shows that higher velocities were recorded at the beginning of the wall jet development, immediately outward the stagnation region of the central jet in all cases. This flow acceleration was induced after the flow deflection and was characterized by increased shear forces and a thin boundary layer. As previously discussed, the central jet’s flow kept its regular structure while the adjacent jets were affected by the interaction of the upstream jets’ flow. This deflection led to a decrease in the velocity recorded at the adjacent jets’ stagnation zone located at
x/
D = 6. As expected from the previous analysis, higher velocities were achieved at the acceleration region induced in the vicinity of the stagnation region of the central jet impinging the 2
D step plate. Therefore, higher local heat transfer rates were expected to be recorded. The velocity magnitude over the plate started to decrease as the radial distance (
x/
D) from the central jet axis increased. This decrease was approximately the same for the three cases, achieving a minimum value at
x/
D = 1. As the central wall jet developed over the target plate, flow interactions occurred due to the collision with the wall-jet of the adjacent jets. These interactions increased the flow turbulence and consequently an increase in velocity was observed, achieving a secondary peak at
x/
D ≈ 3. This location corresponds to the vicinity of the stagnation region of adjacent jets located at the front and back rows. As the results demonstrate, the magnitude of the secondary peak was approximately the same for all cases. Near
x/
D = 4, a decrease in velocity was observed and had to correspond to a stagnation point induced by the collision between the wall jet’s flow. The third velocity peak was identified near the stagnation region of the adjacent jet located at
x/
D = 6, as expected. Comparing the different cases, it seems that the higher velocity was identified for the flat plate case. This shows that the deflection of the adjacent jet flow was stronger for the non-flat plates, leading to a reduction in the local velocity. As the flow went through the outlet, an increase in flow turbulence was also identified due to the interaction of the upstream jets-induced crossflow with the adjacent jets located at
x/
D = 9.
Looking at the left-hand side, the velocity profile shows a peak near
x/
D = −1.5 for the non-flat plate cases. This peak was induced by the increased flow vorticity generated by the collision of the central wall jet with the step surface. This peak is slightly higher for the 1
D step due to the cumulative effect of the deflection of the adjacent jet flow located at
x/
D = −3 and the step corner with the central wall jet. At the bottom of the step, a stagnation point was identified, recording a velocity near zero. For the case of the flat plate case, a peak was recorded near
x/
D = −3 due to the strong interactions between the wall jets of the jets positioned in the front and back row with the one located in the central row. Finally, another maximum velocity was observed at
x/
D = −6, being higher than the one identified at
x/
D = 6, showing that the magnitude of the vortex that induced the deflection of the adjacent jet (
x/
D = −6) and that is identified in
Figure 8, was lower than the vortex that interfered with the jet located at
x/
D = 6. These results demonstrate the complexity of the flow field and the difficulty of obtaining uniform development of the flow over the target surface. These effects were stronger when non-flat target plates were applied.
4.3. Velocity Profile over the Central Jet Axis
The velocity profile at the central jet axis and that adjacent on the right are presented in
Figure 10a,b, respectively. The velocity profile recorded at the jets’ axis shows the effect of the target plate geometry on the jets’ flow development.
Looking at the central jet, the results demonstrate that near zero velocities at the stagnation point were only identified in the 1
D step plate case, while higher velocities were recorded in the case of the flat plate and 2
D step plate. These results show the limitation of the PIV system to measure, with accuracy, the velocities near the target plate. To improve these measurements and to be able to capture the stagnation points, the CCD camera should focus the flow at the surface transition instead of the overall, from the nozzle to the target plate. While the velocity field recorded by the PIV system and presented in
Figure 8 does not allow clear identification of the different jets’ regions, the velocity profile at the jet axis (
Figure 10) shows that 95% of the maximum velocity, the end of the potential core, was achieved at
H/
D near 0.7 for the flat and 2
D step plates and 0.8 for the 1
D step plate. These data demonstrate that the 1
D step induced higher fluctuations of the flow, due to the jets’ flow separation near the step. The vortex previously identified in
Figure 8, highly contributed to this reduction in the potential core length compared with the other cases. These interactions were not observed in the 2
D step case since the step height was similar to the nozzle-to-plate separation. Comparing these values with those obtained at the axis of the adjacent jets, the data show a reduction in the actual length of the potential core. A decrease of 20% was identified in the flat plate case, and 40% and 65% for the 2
D step and 1
D step cases, respectively. These results evidence not only that the adjacent jets were strongly affected by the upstream jets but also that the non-flat plate increased the flow turbulence. The higher decrease was identified in the 1
D step configuration, as expected. The end of the potential core indicates the beginning of the stagnation region that extended from
H/
D near 0.8 to
H/
D = 0.
Considering that the distance between the nozzle and the target plates was small (
H/
D = 2), other jet regions identified by [
57], such as the decaying and acceleration regions, were not observed in the central jet. However, this was not the case for the adjacent jets. The reduction in the potential core length, as described above, was mainly due to the increased magnitude of the primary vortices. The intensity of the flow turbulence increased with more complex surfaces, and a gradual acceleration between the end of the potential core and the stagnation region was observed. In addition, while velocities near zero at the stagnation point were not detected in all central jets, this was not the case for the adjacent jets.
4.4. Average Heat Transfer over a Flat and Non-Flat Plate
The average heat transfer of multiple air jets impinging a flat and non-flat plate is analyzed in this section. The average Nusselt numbers obtained from the heat flux measurements for the flat and non-flat plate cases are summarized in
Table 3, as well as the uncertainty of the measurements.
The results demonstrate that the heat transfer was increased by the non-flat plate. These observations are in agreement with the velocity profiles obtained in the previous sections. Compared with the flat plate, the heat transfer increased about 10% for the case of the 1
D step plate and 20% for the 2
D step plate. As mentioned previously, the step surface increased the turbulence inside the confined space between the nozzle and the target plates. As a consequence, higher velocities were measured by the PIV system compared with the flat plate. This increased turbulence promoted the mixing between the jets’ flow and the surrounding air, increasing the heat transfer. In addition to the overall increase in the flow turbulence, the step induced a deflection of the jets that directly impinged over it and blocked the wall jet development coming from the central jet, inducing a flow recirculation. This phenomenon increased the local heat transfer, which was also observed by others [
10]. This observation can be explained by the larger stagnation zone of the central jet compared with the other cases, which induced higher heat transfer rates. According to [
59], the heat transfer mechanism in the stagnation region is caused by the dynamic behavior of recirculation zones characterized by stagnant heated fluid and the sweeping of the heated fluid. Thus, these circulation zones were expected to be identified with a stronger intensity in the 2
D step plate. To support these conclusions, more analysis with smaller step dimensions is needed.