Distributed Event-Based Control of Hierarchical Leader-Follower Networks with Time-Varying Layer-To-Layer Delays
Abstract
:1. Introduction
2. Preliminaries
2.1. Basic Theory on Graphs and Matrices
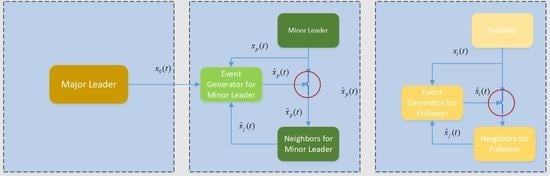
2.2. System Description
3. Main Results
3.1. Event-Based Control for Consensus of HLFNs
3.2. Event-Based Control for Consensus of HLFNs with Layer-to-Layer Delays
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, Y.; Ma, J.; Wang, L. Consensus of hybrid multi-agent systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1359–1365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Zhang, K.; Xie, W.C. Consensus of multi-agent systems via hybrid impulsive protocols with time-delay. Nonlinear Anal. Hybrid Syst. 2018, 30, 134–146. [Google Scholar] [CrossRef]
- Yan, Z.; Pan, X.; Yang, Z.; Yue, L. Formation Control of Leader-Following Multi-UUVs With Uncertain Factors and Time-Varying Delays. IEEE Access 2019, 7, 118792–118805. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, X.; Cong, Y.; Li, H. Scalability Analysis of Algebraic Graph-Based Multi-UAVs Formation Control. IEEE Access 2019, 7, 129719–129733. [Google Scholar] [CrossRef]
- Tanner, H.G.; Christodoulakis, D.K. Decentralized cooperative control of heterogeneous vehicle groups. Robot. Auton. Syst. 2007, 55, 811–823. [Google Scholar] [CrossRef]
- Liang, C.D.; Wang, L.; Yao, X.Y.; Liu, Z.W. Multi-target tracking of networked heterogeneous collaborative robots in task space. Nonlinear Dynam. 2019, 1–15. [Google Scholar] [CrossRef]
- HYazdani, S.; Haeri, M. Flocking of multi-agent systems with multiple second-order uncoupled linear dynamics and virtual leadere. IET Control Theory Appl. 2016, 10, 853–860. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Su, H. Self-triggered leader-following consensus of multi-agent systems with input time delay. Neurocomputing 2019, 330, 70–77. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, P.; Zhu, J.; Zhang, L. Adaptive consensus control of leader-following systems with transmission nonlinearities. Int. J. Control 2019, 92, 317–328. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Lu, Q. Fixed-Time Leader-Following Consensus for Multiple Wheeled Mobile Robots. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef] [PubMed]
- Nagy, M.; Akos, Z.; Biro, D.; Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 2010, 464, 890. [Google Scholar] [CrossRef] [PubMed]
- He, D.X.; Xu, G.H.; Guan, Z.H.; Chi, M.I. Hybrid coordination of multi-agent networks with hierarchical leaders. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 110–119. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Chandrasekar, A.; Laksmanan, S.; Park, J.H. State estimation of memristor-based recurrent neural networks with time-varying delays based on passivity theory. Complexity 2014, 19, 32–43. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Ding, X.; Zhao, G. Leader–Follower Consensus of Multiagent Systems With Time Delays Over Finite Fields. IEEE Trans. Cybern. 2018, 49, 3203–3208. [Google Scholar] [CrossRef]
- Zhao, G.; Hua, C.; Guan, X. Distributed Event-Triggered Consensus of Multiagent Systems With Communication Delays: A Hybrid System Approach. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Y.; Wang, S. Distributed adaptive consensus control for networked robotic manipulators with time-varying delays under directed switching topologies. Peer-to-Peer Netw. Appl. 2019. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Chen, T.; Hao, F. Event-triggered bipartite consensus for multi-agent systems: A Zeno-free analysis. IEEE Trans. Autom. Control 2019. [Google Scholar] [CrossRef]
- Yi, X.; Yang, T.; Wu, J.; Johansson, K.H. Distributed event-triggered control for global consensus of multi-agent systems with input saturation. Automatica 2019, 310, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Song, Q.; Lu, G. Event-triggered bipartite leader-following consensus of second-order nonlinear multi-agent systems under signed digraph. IEEE J. Frankl. Inst. 2019, 356, 6591–6609. [Google Scholar] [CrossRef]
- Mirollo, R.E.; Strogatz, S.H. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 1990, 50, 1645–1662. [Google Scholar] [CrossRef]
- Strogatz, S.H. From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Phys. D Nonlinear Phenom. 2000, 143, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Preciado, V.M.; Verghese, G.C. Synchronization in Generalized Erd ö sR é nyi Networks of Nonlinear Oscillators. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 4628–4633. [Google Scholar]
- Sepulchre, R.; Paley, D.; Leonard, N. Collective motion and oscillator synchronization. Lect. Notes Control Inf. Sci. 2004, 309, 466–469. [Google Scholar]
- Rojo-Rodriguez, E.G.; Garcia, O.; Ollervides, E.J.; Zambrano Robledo, P.C. Robust Consensus-Based Formation Flight for Multiple Quadrotors. J. Intell. Robot. Syst. 2019, 93, 213–226. [Google Scholar] [CrossRef]
- Masroor, S.; Peng, C. Event triggered non-inverting chopper fed networked DC motor speed synchronization. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 911–929. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, R.; Yan, H. Distributed event-triggered control for consensus of multi-agent systems. J. Frankl. Inst. 2015, 352, 3476–3488. [Google Scholar] [CrossRef]
- Wang, Y.W.; Lei, Y.; Bian, T.; Guan, Z.H. Distributed Control of Nonlinear Multiagent Systems With Unknown and Nonidentical Control Directions via Event-Triggered Communication. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Jian, L.; Hu, J.; Wang, J. New Event-based Control for Sampled-data Consensus of Multi-agent Systems. Int. J. Control Autom. Syst. 2019, 17, 1107–1116. [Google Scholar] [CrossRef]
- Lai, Q.; Didier Kamdem Kuate, P.; Liu, F.; Ho-Ching Iu, H. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2019. [Google Scholar] [CrossRef]
- Lai, Q.; Akgul, A.; Li, C.; Xu, G.; Çavuşoğlu, Ü. A New Chaotic System with Multiple Attractors: Dynamic Analysis, Circuit Realization and S-Box Design. Entropy 2018, 20, 12. [Google Scholar] [CrossRef] [Green Version]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Solitons Fractals 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Ge, M.F.; Liu, Z.W.; Wen, G.; Yu, X.; Huang, T. Hierarchical Controller-Estimator for Coordination of Networked Euler-Lagrange Systems. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Sun, C.; Li, H. Event-based leader-following consensus of multi-agent systems with switching topologies. In Proceedings of the Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 7511–7516. [Google Scholar]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.-H.; Xu, M.; Ge, M.-F.; Ding, T.-F.; Qi, F.; Li, M. Distributed Event-Based Control of Hierarchical Leader-Follower Networks with Time-Varying Layer-To-Layer Delays. Energies 2020, 13, 1808. https://doi.org/10.3390/en13071808
Xu G-H, Xu M, Ge M-F, Ding T-F, Qi F, Li M. Distributed Event-Based Control of Hierarchical Leader-Follower Networks with Time-Varying Layer-To-Layer Delays. Energies. 2020; 13(7):1808. https://doi.org/10.3390/en13071808
Chicago/Turabian StyleXu, Guang-Hui, Meng Xu, Ming-Feng Ge, Teng-Fei Ding, Feng Qi, and Meng Li. 2020. "Distributed Event-Based Control of Hierarchical Leader-Follower Networks with Time-Varying Layer-To-Layer Delays" Energies 13, no. 7: 1808. https://doi.org/10.3390/en13071808