Comparison of Nonlinear Wave-Loading Models on Rigid Cylinders in Regular Waves
Abstract
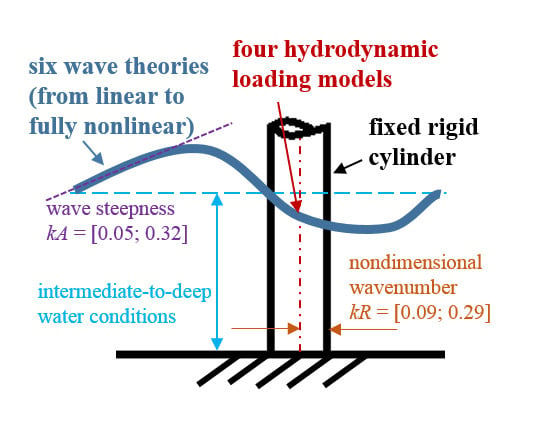
:1. Introduction
2. Methodology
2.1. Wave Kinematics
2.2. Hydrodynamic Loading Models
2.3. Experimental Grid
3. Results and Discussion
3.1. Secondary Load Cycle
3.2. Distinction between the Nonlinearities in Wave Kinematics and Loading Models
3.3. Non-Monotonic Experimental Behavior Over Increasing Steepness
3.4. Influence of the Number
3.5. Behavior of the Numerical Models in Reference to the ()-grid and Wave Theory Limits
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Norwegian Petroleum Directorate. NPD Annual Report 1992; Technical Report; Norwegian Petroleum Directorate: Stavanger, Norway, 1993. [Google Scholar]
- Chaplin, J.R.; Rainey, R.C.; Yemm, R. Ringing of a vertical cylinder in waves. J. Fluid Mech. 1997, 350, 119–147. [Google Scholar] [CrossRef]
- Grue, J.; Bjorshol, G.; Strand, Ø. Higher harmonic wave exciting forces on a vertical cylinder. In Mechanics and Applied Mathematics; Preprint series No. 2; University of Oslo: Oslo, Norway, 1993; pp. 1–30. Available online: http://urn.nb.no/URN:NBN:no-52740 (accessed on 10 September 2019).
- Grue, J.; Huseby, M. Higher harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 2002, 24, 203–214. [Google Scholar] [CrossRef]
- Rainey, R.C. Weak or strong nonlinearity: The vital issue. J. Eng. Math. 2007, 58, 229–249. [Google Scholar] [CrossRef]
- Paulsen, B.T.; Bredmose, H.; Bingham, H.B.; Jacobsen, N.G. Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 2014, 755, 1–34. [Google Scholar] [CrossRef]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Bredmose, H.; Schlütter, F.; Qvist, J.; Bergua, R.; Yde, A.; Anders, T.; et al. OC5 Project Phase Ib: Validation of Hydrodynamic Loading on a Fixed, Flexible Cylinder for Offshore Wind Applications. Energy Procedia 2016, 94, 82–101. [Google Scholar] [CrossRef]
- Krokstad, J.R.; Solaas, F. Study of Nonlinear Local Flow. In Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, WA, USA, 28 May–2 June 2000; Volume 4, pp. 449–454. [Google Scholar]
- Suja-Thauvin, L.; Krokstad, J.R.; Bachynski, E.E.; de Ridder, E.J. Experimental results of a multimode monopile offshore wind turbine support structure subjected to steep and breaking irregular waves. Ocean. Eng. 2017, 146, 339–351. [Google Scholar] [CrossRef]
- Gurley, K.R.; Kareem, A. Simlulation of ringing in offshore systems under viscous loads. J. Eng. Mech. 1998, 124, 582–586. [Google Scholar] [CrossRef]
- Waisman, F.; Gurley, K.R.; Grigoriu, M.; Kareem, A. Non-Gaussian Model for Ringing Phenomena in Offshore Structures. J. Eng. Mech. 2002, 128, 730–741. [Google Scholar] [CrossRef] [Green Version]
- Marino, E.; Lugni, C.; Borri, C. A novel numerical strategy for the simulation of irregular nonlinear waves and their effects on the dynamic response of offshore wind turbines. Comput. Methods Appl. Mech. Eng. 2013, 255, 275–288. [Google Scholar] [CrossRef]
- Marino, E.; Lugni, C.; Borri, C. The role of the nonlinear wave kinematics on the global responses of an OWT in parked and operating conditions. J. Wind Eng. Ind. Aerodyn. 2013, 123, 363–376. [Google Scholar] [CrossRef]
- Marino, E.; Lugni, C.; Stabile, G.; Borri, C. Coupled dynamic simulations of offshore wind turbines using linear, weakly and fully nonlinear wave models: The limitations of the second-order wave theory. In Proceedings of the 9th International Conference on Structural Dynam, Porto, Portugal, 30 June–2 July 2014; pp. 3603–3610. [Google Scholar]
- Schløer, S.; Bredmose, H.; Bingham, H.B. The influence of fully nonlinear wave forces on aero-hydro-elastic calculations of monopile wind turbines. Mar. Struct. 2016, 50, 162–188. [Google Scholar] [CrossRef]
- Morison, J.; O’Brien, M.; Johnson, J.; Schaaf, S. The Force Exerted by Surface Waves on Piles. Pet. Trans. AIME 1950, 189, 149–154. [Google Scholar] [CrossRef]
- Rainey, R.C. A new equation for calculating wave loads on offshore structures. J. Fluid Mech. 1989, 204, 295–324. [Google Scholar] [CrossRef]
- Rainey, R.C. Slender-body expressions for the wave load on offshore structures. Proc. Math. Phys. Sci. 1995, 450, 391–416. [Google Scholar] [CrossRef]
- Malenica, S.; Molin, B.; Malenica, Š.; Molin, B. Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 1995, 302, 203–229. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Newman, J.N.; Vinje, T. Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 1995, 289, 179–198. [Google Scholar] [CrossRef]
- Stansberg, C. Comparing ringing loads from experiments with cylinder of different diameters—An experimental study. 1997. [Google Scholar]
- Swan, C.; Bashir, T.; Gudmestad, O. Nonlinear inertial loading. Part I: Accelerations in steep 2-D water waves. J. Fluids Struct. 2002, 16, 391–416. [Google Scholar] [CrossRef]
- Bredmose, H.; Mariegaard, J.; Paulsen, B.T.; Jensen, B.; Schløer, S.; Larsen, T.; Kim, T.; Hansen, A.M. The Wave Loads Project; Technical Report; DTU Wind Energy: Roskilde, Denmark, 2013. [Google Scholar]
- Kristiansen, T.; Faltinsen, O.M. Higher harmonic wave loads on a vertical cylinder in finite water depth. J. Fluid Mech. 2017, 833, 773–805. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, S.K. Hydrodynamics of Offshore Structures. 1. Offshore Structures—Hydrodynamics I.; Springer: Berlin/Heidelberg, Germany, 1987; p. 435. [Google Scholar]
- Rienecker, M.M.; Fenton, J.D. A Fourier approximation method for steady water waves. J. Fluid Mech. 1981, 104, 119–137. [Google Scholar] [CrossRef]
- Marino, E. An Integrated Nonlinear Wind-Waves Model for Offshore Wind Turbines; Firenze University Press: Firenze, Italy, 2010; p. 201. [Google Scholar]
- Marino, E.; Borri, C.; Peil, U. A fully nonlinear wave model to account for breaking wave impact loads on offshore wind turbines. J. Wind Eng. Ind. Aerodyn. 2011, 99, 483–490. [Google Scholar] [CrossRef]
- Marino, E.; Borri, C.; Lugni, C. Influence of wind–waves energy transfer on the impulsive hydrodynamic loads acting on offshore wind turbines. J. Wind Eng. Ind. Aerodyn. 2011, 99, 767–775. [Google Scholar] [CrossRef]
- Grilli, S.T.; Svendsen, I. Corner problems and global accuracy in the boundary element solution of nonlinear wave flows. Eng. Anal. Bound. Elem. 1990, 7, 178–195. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.; Cokelet, E. The Deformation of Steep Surface Waves on Water. I. A Numerical Method of Computation. Proc. R. Soc. A 1976, 350, 1–26. [Google Scholar] [CrossRef]
- Newman, J.N. Nonlinear Scattering of Long Waves by a Vertical Cylinder. In Waves Nonlinear Processes in Hydrodynamics; Grue, J., Gjevik, B., Weber, J.E., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1996; pp. 91–102. [Google Scholar]
- Faltinsen, O.M. Ringing loads on a slender vertical cylinder of general cross-section. J. Eng. Math. 1999, 35, 199–217. [Google Scholar] [CrossRef]
- International Electrotechnical Commission (IEC). INTERNATIONAL STANDARD IEC 61400-3. In Wind Turbines—Part 3: Design Requirements for Offshore Wind Turbines; IEC: Geneva, Switzerland, 2009. [Google Scholar]
- Mockute, A.; Marino, E.; Lugni, C.; Borri, C. Comparison of hydrodynamic loading models for vertical cylinders in nonlinear waves. Procedia Eng. 2017, 199, 3224–3229. [Google Scholar] [CrossRef]
- Huseby, M.; Grue, J. An experimental investigation of higher-harmonic wave forces on a vertical cylinder. J. Fluid Mech. 2000, 414, 75–103. [Google Scholar] [CrossRef]












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mockutė, A.; Marino, E.; Lugni, C.; Borri, C. Comparison of Nonlinear Wave-Loading Models on Rigid Cylinders in Regular Waves. Energies 2019, 12, 4022. https://doi.org/10.3390/en12214022
Mockutė A, Marino E, Lugni C, Borri C. Comparison of Nonlinear Wave-Loading Models on Rigid Cylinders in Regular Waves. Energies. 2019; 12(21):4022. https://doi.org/10.3390/en12214022
Chicago/Turabian StyleMockutė, Agota, Enzo Marino, Claudio Lugni, and Claudio Borri. 2019. "Comparison of Nonlinear Wave-Loading Models on Rigid Cylinders in Regular Waves" Energies 12, no. 21: 4022. https://doi.org/10.3390/en12214022