1. Introduction
The analysis of time-frequency of vibration signals is one of the most effective and important methods for fault diagnosis of rotating machinery, since the vibration signal includes massive information that reflects the running state of rotating machinery [
1]. The empirical mode decomposition (EMD) is one of most commonly used methods for signal processing in the time-frequency domain. EMD can decompose a complex signal into the finite intrinsic mode functions (IMF) based on the local characteristic time scale of signals, and each IMF represents one intrinsic vibration mode of the original signal. Then the characteristic information of the signal can be extracted by analyzing such stationary stable IMFs [
2]. EMD has attracted increasing attention since it appeared [
3,
4,
5], and it has been widely used in economics, biomedicine and engineering science fields, especially for fault diagnosis. Ali et al. [
6] applied the EMD method and artificial neural network in fault diagnosis of rolling bearings automatically. Xue et al. [
7] presented an adaptive, fast EMD method and applied it to rolling bearings fault diagnosis. Yu et al. [
8] introduced various applications of EMD in fault diagnosis. Cheng et al. [
9] combined EMD with a Hilbert transform to conduct the recognition for mode parameters. Then, they introduced how to apply the EMD to the fault diagnosis for local rub-impact of rotors [
10]. Rilling [
11] investigates how the EMD behaves under the case of a composite two-tone signal.
Though EMD has been commonly utilized in reality, some shortcomings are exposed, including mode mixing, end effects, stop criteria of IMF, over-envelope and under-envelope. These deficiencies normally restrict the further promotion and application of EMD [
12]. Since the criterion to judge IMF is that the average value of its upper and lower envelope spectrums is zero in the EMD method, but in the real decomposition process, that average value is impossible to be zero due to the disturbance of cubic spline interpolation, the influence of end effect and adopted frequency. Thus, it is necessary to define a valid stop criterion for the decomposition process in engineering, namely the stop criterion problem of IMF for the EMD method, also named as the sifting stop criterion. Some researchers have attempted to improve the efficiency of EMD. Among them, Pustelnik [
13] mainly developed an alternative to the sifting process for EMD, based on non-smooth convex optimization allowing integration flexibility in the criteria, proposed algorithm and its convergence guarantees.
Mode mixing means that one IMF contains vastly different characteristic time scales, or similar characteristic time scales that are distributed in different IMFs, which results in the waveform mixing of the two adjacent IMFs. These mixing modes influence each other so that it is difficult to identify them. Mode mixing is the fatal flaw of EMD. It makes the physical significance of IMF components uncertain finally, which influences the correctness of signal decomposition and seriously restricts its application in engineering [
14].
Until now, various methods have been developed to restrain the mode-mixing problem in the EMD. Zhao [
15] directly filtered abnormal information related to the IMF and fitted filtered data segment by spline interpolation, but it only proved to dispose the mode mixing problems caused by a known transient abnormity. The masking signal method [
16] and the high frequency harmonic method [
17] are simple and effective, but they are susceptible to distortion and need to be reprocessed for practical engineering signals.
The ensemble empirical mode decomposition (EEMD) presented by Huang is generally considered an effective one [
18]. EEMD takes advantage of the statistical characteristics of white Gaussian noise while frequency is uniformly distributed, so the signal after adding white Gaussian noise shows continuity in different scales, which solved the mode mixing problem to some extent. However, it also raised some other issues. For example, the number and the amplitude of white noises which are added in the signal are greatly subjective, and the EEMD sacrifices some adaptivity. In addition, although the number and the amplitude of added white noises are chosen reasonably, the mode mixing in low frequency may be aroused artificially while high-frequency mode mixing is restricted [
19]. Moreover, the algorithm of the EEMD method is complex and it takes a long time to run the program, which will restrict its application on the signal process that demands to be processed in real-time. Accordingly, some researchers presented improved methods to overcome the deficiencies of EEMD. Among them, Lei [
20] proposed adaptive EEMD to improve its adaptivity. Zheng [
21] developed partial EEMD and Tan [
22] presented multi-resolution EMD to solve mode mixing problem. Mohammad [
23] uses approximate entropy and mutual information to improve EEMD to generate statistical features in order to increase the performance of early fault appearance detection, as well as the fault type and severity estimation.
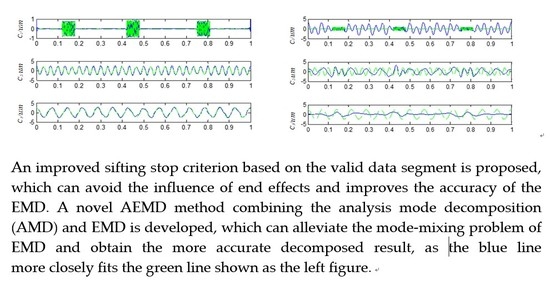
In this paper, a new sifting stop criterion was proposed based on valid data segments to solve the problem of sifting stop criteria in the EMD, and an improved method, namely AEMD, combined the analysis mode decomposition (AMD) and EMD. It was developed to solve the mode-mixing problem. The sifting stop criteria and AEMD proposed were applied to a simulation signal and an engineering case to illustrate the validity and superiority of the proposed method. The structure of the paper is as follows:
Section 2 introduces the basic principles of EMD;
Section 3 narrates the proposed sifting stop criteria based on valid data segment and compares it with the original one; in
Section 4, the principle and steps of AEMD are expounded firstly, then applied to decompose simulation signals and a rotor vibration signal, and it is compared with the EMD and EEMD methods; finally,
Section 5 draws a brief conclusion of current work.
2. Basic Principles of EMD
EMD refers to a “sifting” process, in which, the component with the smallest extreme time feature scale is sifted out firstly, then those with larger extreme time feature scales, and the component with the largest feature scales are finally sifted out. That is to say, the average frequency of IMF components obtained from the EMD is reduced gradually, and the main steps of the EMD are introduced as follows [
24]:
(1) Firstly, identify all the local maximum points and minimum points of original signal
, then match the upper and lower envelope spectrums of extreme points with cubic spline line respectively. Furthermore, ensure that the signal
is between the upper and lower envelope spectrums; (2) calculate the local mean of upper and lower envelope spectrums, denoted as
; (3) calculate the first component
according to Equation (1):
(4) Judge that whether
can satisfy the conditions to be an IMF. If not,
should be treated as an original signal to repeat steps (1), (2) and (3) until
can meet the conditions, designated as
.
is the first IMF component after decomposition. (5) Separate
from the signal
, i.e.,
. (6) Treat
as an original signal to repeat steps (1)–(5), and after
n cycles,
n IMF components and 1 residual value
can be derived; i.e.,
Then, the original signal
can be expressed as:
where
ci refers to the
ith IMF component and
rn is the residual function.
This cycle comes to the end when rn becomes a monotonic function, but in the real decomposition process, when rn meets the conditions of monotonic function, the cycle number is usually large, and the number of IMF components will be too large. Furthermore, a mass of EMD tests have revealed that most of these final components obtained from EMD are false IMF components, without substantive physical significance. Thus, a good sifting stop criterion can not only improve the decomposition efficiency, but also increase the decomposition accuracy.
The stop criteria of decomposition process proposed by Huang was realized by limiting the standard deviation of the two adjacent IMFs and the sifting times are eventually controlled by the iteration threshold
Sd [
25]. In particular,
Sd is defined as:
where
T refers to the time span of a signal,
and
denote the two adjacent processing sequences in the process of EMD and the value of
is usually between 0.2 and 0.3.
It is of great significance to determine reasonable iteration threshold . If the threshold is too small, the computational cost will increase greatly and the IMF components finally obtained will be of no significance; while if it is too large, it will be difficult to satisfy the condition of IMF.
3. The Sifting Stop Criteria Based on the Valid Data Segment
The sifting stop criteria of IMF proposed by Huang is valid for most cases, but there are some problems; it can be noted from Equation (3) that when hk(t) = 0, the iteration threshold will become an uncertain value. It is evidently inappropriate if the iteration threshold is used to control sifting number at the time. In addition, the sifting stop criteria ignored the influence of end effect. Consequently, the decomposition result may produce errors if the distorted endpoint data are adopted. In most cases, the end effect of EMD is obvious, though some effective measures will been taken to restrain it, the end effect still exists.
In this paper, an improved sifting stop criterion of IMF based on the valid data segment is proposed, where the valid data segment means the residual data segment after kicking out the distorted endpoint data. The sifting stop criteria fully consider the influence of end effect to sifting stop criteria, and only use the valid data segment to calculate the iteration threshold. The sifting stop criterion is expressed as follows:
If
hk(
t) is an IMF, it satisfies the following inequality:
where
denotes the valid data segment of the mean curve of upper envelope and lower envelope;
represents the error threshold, which ranges from 0.01 to 0.1.
The EMD is applied to decompose a simulation signal respectively based on the proposed sifting stop criterion and the traditional one below. The simulation signal is
The simulation signal consists of
x1(
t) and
x2(
t) (as shown in
Figure 1,
Figure 2 and
Figure 3) are the decomposition results by using EMD based on the proposed sifting stop criterion and the traditional one, respectively. It is worth noting that the EMD can efficiently decompose the original signal by using the two sifting stop criteria, but it is clear from the two edges of these two figures that the decomposition result
c1 and
c2 in
Figure 2 are more accurate than
imf1 and
imf2 in
Figure 3, which show an evident end effect.
Figure 4 plots the vibration signal of a real gear with broken teeth. The number of gear teeth
; module
; the rotating frequency
. EMD based on the proposed sifting stop criteria is used to decompose the vibration signal of a gear, and obtain five IMFs. The first IMF
imf1 contains massive fault information of the gear. Note from its time domain graph (see
Figure 5) that the waveform of
imf1 presents an obvious modulation feature, and its cycle of modulation wave (
T, approximately 0.074 s) accordingly had a frequency of about 13.6 Hz, which is exactly the rotating frequency of the faulty gear. Thus, it can be concluded that the fault information has been exacted from the vibration signal of the practical gears by using the proposed sifting stop criterion.
5. Conclusions
In this paper, an improved sifting stop criterion based on valid data segment was proposed. Compared with the traditional one, results indicated that the newly proposed sifting stop criterion avoids the influence of end effects and improves the correctness of the EMD. In addition, a novel method, namely AEMD, which combines the AMD and EMD, was developed to solve the mode mixing problem of EMD. Model comparison was conducted between the proposed method and the EEMD. It is worth mentioning that both the AEMD and EEMD can effectively restrain the mode mixing, but the AEMD needs less execution time than that of EEMD. The proposed method overcomes some shortcomings of EMD to some extent and makes it better for use in the fault diagnosis of rotating machinery. However, the proposed method has certain imitations; the boundary frequency of AMD method requires human intervention, which means worse adaptivity than EMD. It can achieve better results for more simple signals, but its advantage is not obvious for complex engineering signals, since they take more time than EMD.