Configurational Entropy in Multicomponent Alloys: Matrix Formulation from Ab Initio Based Hamiltonian and Application to the FCC Cr-Fe-Mn-Ni System
Abstract
:1. Introduction
2. Methods
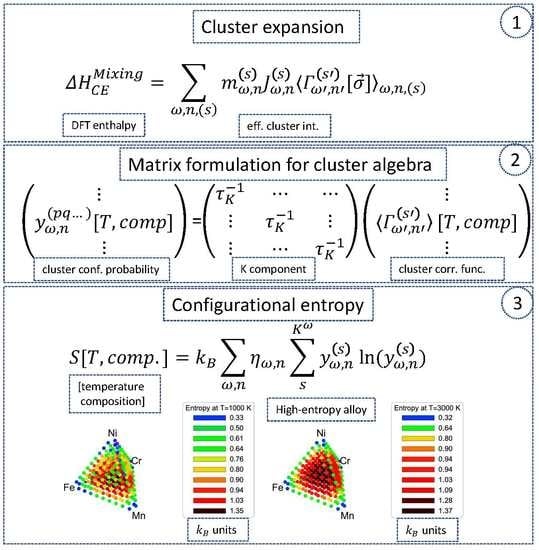
2.1. Matrix Formulation of Cluster Expansion
2.2. Configuration Entropy in the Matrix Formulation
2.3. Computational Details
3. Cluster Probability Functions in FCC Cr-Fe-Mn-Ni Alloys
3.1. Cluster Expansion Hamiltonian for FCC CrFeMnNi
3.2. Full Set of Cluster Decorations
3.3. Four-Body Probability Functions from Monte Carlo Simulations
4. Configuration Entropy in a Cr-Fe-Mn-Ni System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CE | Cluster Expansion |
| CVM | Cluster Variation Method |
| HEA | High-Entropy Alloy |
| K | Number of components in alloy |
| DFT | Density Functional Theory |
| GS | Ground States |
| G | Space Group of the disordered high temperature structure |
| i-th sub-cluster of a maximal cluster | |
| operators acting on the sites of cluster to rearrange the sites i.e., a permutation | |
| site multiplicity of the cluster | |
| sub-cluster multiplicity of the cluster | |
| Number of times a cluster is contained in a supercell structure, generally used for Monte Carlo simulations, for obtaining thermodynamic quantities. |
References
- Cantor, B.; Chang, I.; Knight, P.; Vincent, A. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Gali, A.; George, E.P. Tensile properties of high- and medium-entropy alloys. Intermetallics 2013, 39, 74–78. [Google Scholar] [CrossRef] [Green Version]
- Carroll, R.; Lee, C.; Tsai, C.W.; Yeh, J.W.; Antonaglia, J.; Brinkman, B.A.W.; Leblanc, M.; Xie, X.; Chen, S.; Liaw, P.K.; et al. Experiments and Model for Serration Statistics in Low-Entropy, Medium-Entropy, and High-Entropy Alloys. Sci. Rep. 2015, 5, 16997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, S.; Gao, M.C.; Yang, T.; Liaw, P.K.; Zhang, Y. Phase stability and microstructures of high entropy alloys ion irradiated to high doses. J. Nucl. Mater. 2016, 480, 100–108. [Google Scholar] [CrossRef] [Green Version]
- Lucas, M.S.; Mauger, L.; Muñoz, J.A.; Xiao, Y.; Sheets, A.O.; Semiatin, S.L.; Horwath, J.; Turgut, Z. Magnetic and vibrational properties of high-entropy alloys. J. Appl. Phys. 2011, 109, 07E307. [Google Scholar] [CrossRef]
- Calvo-Dahlborg, M.; Cornide, J.; Tobola, J.; Nguyen-Manh, D.; Wróbel, J.S.; Juraszek, J.; Jouen, S.; Dahlborg, U. Interplay of electronic, structural and magnetic properties as the driving feature of high-entropy CoCrFeNiPd alloys. J. Phys. D Appl. Phys. 2017, 50, 185002. [Google Scholar] [CrossRef]
- Rossiter, P.L.; Wells, P. The dependence of the electrical resistivity on short-range order. J. Phys. C Solid State Phys. 1971, 4, 354–363. [Google Scholar] [CrossRef]
- Spruiell, J.E.; Stansbury, E.E. X-Ray study of short-range order in nickel alloys containing 10.7 and 20.0 at. % Molybdenum. J. Phys. Chem. Solids 1965, 26, 811–822. [Google Scholar] [CrossRef]
- Fisher, J.C. On the strength of solid solution alloys. Acta Metall. 1954, 2, 9–10. [Google Scholar] [CrossRef]
- Fernández-Caballero, A.; Wróbel, J.S.; Mummery, P.M.; Nguyen-Manh, D. Short-Range Order in High Entropy Alloys: Theoretical Formulation and Application to Mo-Nb-Ta-V-W System. J. Phase Equilib. Diffus. 2017, 38, 391–403. [Google Scholar] [CrossRef] [Green Version]
- Santodonato, L.J.; Zhang, Y.; Feygenson, M.; Parish, C.M.; Gao, M.C.; Weber, R.J.K.; Neuefeind, J.C.; Tang, Z.; Liaw, P.K. Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy. Nat. Commun. 2015, 6, 5964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leong, Z.; Wróbel, J.S.; Dudarev, S.L.; Goodall, R.; Todd, I.; Nguyen-Manh, D. The Effect of Electronic Structure on the Phases Present in High Entropy Alloys. Sci. Rep. 2017, 7, 39803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Fontaine, D. Cluster Approach to Order-Disorder Transformations in Alloys. Solid State Phys. 1994, 47, 33–176. [Google Scholar]
- Van de Walle, A.; Asta, M.; Ceder, G. The Alloy Theoretic Automated Toolkit: A User Guide. Calphad Comput. Coupling Phase Diagr. Thermochem. 2002, 26, 539–553. [Google Scholar] [CrossRef]
- Van de Walle, A. Multicomponent multisublattice alloys, nonconfigurational entropy and other additions to the Alloy Theoretic Automated Toolkit. Calphad Comput. Coupling Phase Diagr. Thermochem. 2009, 33, 266–278. [Google Scholar] [CrossRef] [Green Version]
- Wróbel, J.S.; Nguyen-Manh, D.; Lavrentiev, M.Y.; Muzyk, M.; Dudarev, S.L. Phase stability of ternary fcc and bcc Fe-Cr-Ni alloys. Phys. Rev. B 2015, 91, 024108. [Google Scholar] [CrossRef]
- Sanchez, J.M.; de Fontaine, D. The fcc Ising model in the cluster variation approximation. Phys. Rev. B 1978, 17, 2926–2936. [Google Scholar] [CrossRef]
- Finel, A. The cluster variation method and some applications. In Proceedings of NATO Advanced Study Institute on Statics and Dynamics of Alloy Phase Transformations; Turchi, P.E.A., Gonis, A., Eds.; Springer: Rhodes, Greece, 1992; pp. 495–540. [Google Scholar]
- Lu, Z.W.; Wei, S.H.; Zunger, A.; Frota-Pessoa, S.; Ferreira, L.G. First-principles statistical mechanics of structural stability of intermetallic compounds. Phys. Rev. B 1991, 44, 512–544. [Google Scholar] [CrossRef]
- Lechermann, F.; Fähnle, M.; Sanchez, J.M. First-principles investigation of the Ni-Fe-Al system. Intermetallics 2005, 13, 1096–1109. [Google Scholar] [CrossRef]
- Ackermann, H.; Inden, G.; Kikuchi, R. Tetrahedron approximation of the cluster variation method for b.c.c. alloys. Acta Metall. 1989, 37, 1–7. [Google Scholar] [CrossRef]
- Tepesch, P.D.; Asta, M.; Ceder, G. Computation of configurational entropy using Monte Carlo probabilities in cluster-variation method entropy expressions. Model. Simul. Mater. Sci. Eng. 1998, 6, 787–797. [Google Scholar] [CrossRef]
- Kumar, N.K.; Li, C.; Leonard, K.; Bei, H.; Zinkle, S. Microstructural stability and mechanical behavior of FeNiMnCr high entropy alloy under ion irradiation. Acta Mater. 2016, 113, 230–244. [Google Scholar] [CrossRef] [Green Version]
- Hart, G.L.W.; Forcade, R.W. Algorithm for generating derivative structures. Phys. Rev. B 2008, 77, 224115. [Google Scholar] [CrossRef]
- Taggart, G.B. Generalized Flinn operators with applications to multi-component alloys. J. Phys. Chem. Solids 1973, 34, 1917–1925. [Google Scholar] [CrossRef]
- Cenedese, P.; Gratias, D. Multicomponent formalism in the mean-field approximation: A geometric interpretation of Chebychev polynomials. Phys. A Stat. Mech. Appl. 1991, 179, 277–287. [Google Scholar] [CrossRef]
- Sluiter, M.H.; Kawazoe, Y. Invariance of truncated cluster expansions for first-principles alloy thermodynamics. Phys. Rev. B 2005, 71, 1–2. [Google Scholar] [CrossRef]
- Blum, V.; Zunger, A. Prediction of ordered structures in the bcc binary systems of Mo, Nb, Ta, and W from first-principles search of approximately 3,000,000 possible configurations. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 3–6. [Google Scholar] [CrossRef]
- Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev. 1951, 81, 988–1003. [Google Scholar] [CrossRef]
- Barker, J.A. Methods of Approximation in the Theory of Regular Mixtures. Proc. R. Soc. A Math. Phys. Eng. Sci. 1953, 216, 45–56. [Google Scholar]
- Gratias, D.; Sanchez, J.; De Fontaine, D. Application of group theory to the calculation of the configurational entropy in the cluster variation method. Phys. A Stat. Mech. Appl. 1982, 113, 315–337. [Google Scholar] [CrossRef]
- Wróbel, J.S.; Nguyen-Manh, D.; Kurzydłowski, K.J.; Dudarev, S.L. A first-principles model for anomalous segregation in dilute ternary tungsten-rhenium-vacancy alloys. J. Phys. Condens. Matter 2017, 29, 145403. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Van de Walle, A.; Asta, M. Self-driven lattice-model Monte Carlo simulations of alloy thermodynamic properties and phase diagrams. Model. Simul. Mater. Sci. Eng. 2002, 10, 521–538. [Google Scholar] [CrossRef] [Green Version]
- Lavrentiev, M.Y.; Wróbel, J.S.; Nguyen-Manh, D.; Dudarev, S.L.; Ganchenkova, M.G. Magnetic cluster expansion model for random and ordered magnetic face-centered cubic Fe-Ni-Cr alloys. J. Appl. Phys. 2016, 120, 043902. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lu, Z.; Ma, S.; Liaw, P.; Tang, Z.; Cheng, Y.; Gao, M. Guidelines in predicting phase formation of high-entropy alloys. MRS Commun. 2014, 4, 57–62. [Google Scholar] [CrossRef]




| n | Coordinates | ECI (meV/atom) | n | Coordinates | ECI (meV/atom) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | (0) | (1,1,1) | +0.00 | 3 | 1 | (1,1,1) | (1,1,1) | +0.20 |
| (1) | +0.11 | (2,1,1) | (3/2,1,1/2) | +0.90 | |||||
| (2) | −0.04 | (3,1,1) | (1,3/2,1/2) | +1.60 | |||||
| (3) | −0.01 | (2,2,1) | −3.40 | ||||||
| 2 | 1 | (1,1) | (1,1,1) | +9.40 | (3,2,1) | −0.50 | |||
| (2,1) | (1,3/2,3/2) | −0.10 | (3,3,1) | +1.20 | |||||
| (3,1) | +3.40 | (2,2,2) | +0.20 | ||||||
| (2,2) | +0.40 | (3,2,2) | +2.00 | ||||||
| (3,2) | +1.30 | (3,3,2) | −0.50 | ||||||
| (3,3) | +6.00 | (3,3,3) | +0.00 | ||||||
| 2 | 2 | (1,1) | (1,1,1) | −9.20 | 3 | 2 | (1,1,1) | (1,1,1) | −0.60 |
| (2,1) | (1,1,0) | +0.40 | (2,1,1) | (1,3/2,1/2) | +1.00 | ||||
| (3,1) | −4.40 | (3,1,1) | (1,1,0) | +0.90 | |||||
| (2,2) | −11.60 | (1,2,1) | −1.80 | ||||||
| (3,2) | −3.50 | (2,2,1) | +2.30 | ||||||
| (3,3) | −8.80 | (3,2,1) | −0.70 | ||||||
| 2 | 3 | (1,1) | (1,1,1) | 0.90 | (1,3,1) | −2.10 | |||
| (2,1) | (2,3/2,3/2) | 2.60 | (2,3,1) | −0.30 | |||||
| (3,1) | 3.50 | (3,3,1) | −0.60 | ||||||
| (2,2) | 1.60 | (2,1,2) | −6.30 | ||||||
| (3,2) | −0.30 | (3,1,2) | −1.20 | ||||||
| (3,3) | 0.10 | (2,2,2) | -0.60 | ||||||
| 2 | 4 | (1,1) | (1,1,1) | −0.40 | (3,2,2) | −0.10 | |||
| (2,1) | (2,1,2) | 2.40 | (2,3,2) | +1.60 | |||||
| (3,1) | 1.20 | (3,3,2) | +0.60 | ||||||
| (2,2) | 0.50 | (3,1,3) | −2.00 | ||||||
| (3,2) | 0.60 | (3,2,3) | +0.30 | ||||||
| (3,3) | −0.80 | (3,3,3) | −1.40 | ||||||
| 2 | 5 | (1,1) | (1,1,1) | −1.00 | 4 | 1 | (1,1,1,1) | (1,1,1) | −3.30 |
| (2,1) | (1,3/2,−1/2) | −3.50 | (2,1,1,1) | (3/2,3/2,1) | +2.00 | ||||
| (3,1) | −2.00 | (3,1,1,1) | (3/2,1,1/2) | +0.70 | |||||
| (2,2) | 0.20 | (2,2,1,1) | (1,3/2,1/2) | −2.90 | |||||
| (3,2) | 0.90 | (3,2,1,1) | +0.60 | ||||||
| (3,3) | 0.40 | (3,3,1,1) | +0.70 | ||||||
| 2 | 6 | (1,1) | (1,1,1) | 0.80 | (2,2,2,1) | −0.60 | |||
| (2,1) | (2,2,0) | 2.10 | (3,2,2,1) | −1.10 | |||||
| (3,1) | 1.00 | (3,3,2,1) | +1.30 | ||||||
| (2,2) | −2.70 | (3,3,3,1) | +2.60 | ||||||
| (3,2) | −1.30 | (2,2,2,2) | −0.50 | ||||||
| (3,3) | 0.50 | (3,2,2,2) | +4.90 | ||||||
| (3,3,2,2) | +1.00 | ||||||||
| (3,3,3,2) | −1.60 | ||||||||
| (3,3,3,3) | −1.70 |
| Maximal Cluster | Permutation Operators | Sub-Cluster | |||
|---|---|---|---|---|---|
| 1 | 1 | −1 | |||
| 1 | 2 | 11 | |||
| 6 | 1 | −6 | |||
| 1 | 2 | 5 | |||
| 3 | 1 | −3 | |||
| 1 | 2 | 23 | |||
| 12 | 1 | −12 | |||
| 1 | 2 | 11 | |||
| 6 | 1 | −6 | |||
| 1 | 2 | 23 | |||
| 12 | 1 | −12 | |||
| 1 | 2 | 7 | |||
| 4 | 1 | −4 | |||
| 1 | 3 | −13 | |||
| 6 | 3 | 18 | |||
| 8 | 1 | −8 | |||
| 1 | 3 | −19 | |||
| 1 | 1 | 9 | |||
| 6 | 2 | 18 | |||
| 12 | 1 | −12 | |||
| 1 | 4 | −5 | |||
| 6 | 6 | 6 | |||
| 8 | 4 | 0 | |||
| 2 | 1 | −2 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Caballero, A.; Fedorov, M.; Wróbel, J.S.; Mummery, P.M.; Nguyen-Manh, D. Configurational Entropy in Multicomponent Alloys: Matrix Formulation from Ab Initio Based Hamiltonian and Application to the FCC Cr-Fe-Mn-Ni System. Entropy 2019, 21, 68. https://doi.org/10.3390/e21010068
Fernández-Caballero A, Fedorov M, Wróbel JS, Mummery PM, Nguyen-Manh D. Configurational Entropy in Multicomponent Alloys: Matrix Formulation from Ab Initio Based Hamiltonian and Application to the FCC Cr-Fe-Mn-Ni System. Entropy. 2019; 21(1):68. https://doi.org/10.3390/e21010068
Chicago/Turabian StyleFernández-Caballero, Antonio, Mark Fedorov, Jan S. Wróbel, Paul M. Mummery, and Duc Nguyen-Manh. 2019. "Configurational Entropy in Multicomponent Alloys: Matrix Formulation from Ab Initio Based Hamiltonian and Application to the FCC Cr-Fe-Mn-Ni System" Entropy 21, no. 1: 68. https://doi.org/10.3390/e21010068