Nonlinear Thermodynamic Analysis and Optimization of a Carnot Engine Cycle
Abstract
:1. Introduction
2. Materials and Methods
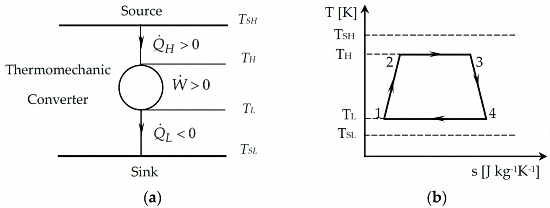
2.1. Model of Carnot Cycle Engine
2.2. Optimization of the CNCA Machine by Using the Entropic Ratio Method
2.2.1. Optimization General Approach
- entering fluxes, which are generally called EC, energy or material consumptions; to them OF 5 corresponds, namely MIN EC (here );
- an useful flux or Useful Effect, UE (here MAX )
- rejects, R, that may be recoverable (RR, recyclable waste), but most often pollutants for the Environment (RP, pollutant rejects); accordingly, OF 6 namely MIN (R).
2.2.2. Particular Results for the Objective Functions MAX , MIN ISH
Maximization of the Power Output of CNCA Engine
Consideration of System Irreversibility
- Condition of transfer entropies equipartition
- Minimization of the entropy production rate of the system
2.3. Optimization of the CNCA Machine by Using the Entropy Production Rate Method
2.3.1. General Statement of the Optimization
- Entropy production rate of the converter
- -
- (, endoreversible)
- -
- (linear dependence on temperature difference)
- -
- (logarithmic dependence on temperature ratio)
- Heat transfer laws at the source and sink
2.3.2. General and Required Condition for the Existence of Optimum Corresponding to MAX
2.3.3. Sequential Optimization of the Engine Power Output
Asymptotic Solution for the Case SC(w) Smaller than kHAH and kLAL
Optimization of the Physical Geometric Dimensions AH, AL, of the System
3. Discussion—Partial Conclusion
- (a)
- For a dissipation law, similar to that reported in [18], Equation (51) becomes:
- (b)
- For a dissipation law as an mth power function of the speed:
4. Extensions—Particular Results
4.1. Optimization Statement on an Entropic Base
4.2. Particularization to Calculate the Various Entropy Production Rates
5. Conclusions
- the maximum power supplied by the engine does not correspond systematically to the minimum entropy production rate;
- equipartition of entropy production rate is not associated to the maximum power delivered by the engine (endoreversible or not).
Author Contributions
Conflicts of Interest
Nomenclature
| A | heat transfer area | m2 |
| a | coefficient dependent of the gas nature | - |
| b | coefficient related to throttling | - |
| c | molecular average speed | m/s |
| mass specific heat at constant pressure | J/kg−K | |
| heat rate capacity of the source | W/K | |
| mass flow rate of the source fluid | kg/s | |
| I | entropic ratio | - |
| K | heat transfer conductance | W/K |
| k | overall heat transfer coefficient | W/m2K |
| Pm, i | instantaneous mean pressure of the gas | Pa |
| ΔP | pressure losses | Pa |
| heat transfer rate | W | |
| S | entropy | J/K |
| entropy rate | W/K | |
| T | temperature | K |
| V | volume | m3 |
| power output of the engine | W | |
| w | characteristic speed | m/s |
Greek symbols
| α | intermediate variable |
| ηC | Carnot cycle efficiency |
| ηex | exergetic efficiency |
| ηI | First Law efficiency |
| ηII | Second Law efficiency |
Subscripts
| C | related to the converter |
| eq | corresponding to equipartition of entropy production between hot-end and cold-end |
| f | friction |
| H | related to the gas at the hot-end |
| L | related to the gas at the cold-end |
| SH | related to the source (hot-end) |
| SHi | related to the source fluid in the hot-end heat exchanger |
| SL | related to the sink (cold-end) |
| T | total |
| thr | throttling |
| 0 | related to ambient conditions |
Superscript
| * | related to optimum |
Acronyms
| C1, C2 | Constraints |
| CHP | Combined Heat and Power |
| CNCA | Carnot–Novikov–Curzon–Ahlborn |
| EC | Energy Consumption |
| FST | Finite Speed Thermodynamics |
| FTT | Finite Time Thermodynamics |
| OF | Objective Function |
| R | Reject |
| UE | Useful Effect |
References and Notes
- Carnot, S. Réflexion Sur la Puissance Motrice du Feu et Des Machines Propres à Développer Cette Puissance; Albert Blanchard: Paris, France, 1953. (In French) [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Conditions. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Feidt, M.; Université de Lorraine, Nancy, France. Personal Communication, 23 February 2013.
- Novikov, I.I. The efficiency of Atomic Power Stations (a review). J. Nucl. Energy 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. (In French) [Google Scholar]
- Chambadal, P. Evolutions et Applications du Concept D’entropie; Dunod: Paris, France, 1963; p. 84. (In French) [Google Scholar]
- Feidt, M. Thermodynamique Optimale en Dimensions Physiques Finies; Hermes, Lavoisier: Paris, France, 2013. [Google Scholar]
- Park, H.; Kim, M.S. Thermodynamic performance Analysis of Sequential Carnot Cycles using Heat Sources with Finite Heat Capacity. Energy 2014, 68, 592–598. [Google Scholar] [CrossRef]
- Mehta, P.; Polkovnikov, A. Efficiency bounds for non-equilibrium heat engines. Ann. Phys. 2012, 332, 110–126. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, Y.; Liu, Y. Performance Optimization of an Irreversible Carnot Refrigerator with Finite Mass Flow Rate. Int. J. Refrig. 2011, 34, 567–572. [Google Scholar] [CrossRef]
- Frikha, S.; Abid, M.S. Performance Optimization of an Irreversible Combined Carnot Refrigerator based on Ecological Criterion. Int. J. Refrig. 2016, 65, 153–165. [Google Scholar] [CrossRef]
- Vaudrey, A.; Lanzetta, F.; Feidt, M. HB reitlinger and the origins of the efficiency at maximum power formula for heat engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Petrescu, S.; Costea, M.; Feidt, M.; Ganea, I.; Boriaru, N. Advanced Irreversible Thermodynamics of Processes with Finite Speed and Finite Dimensions; Editura AGIR: Bucharest, Romania, 2015. [Google Scholar]
- Petrescu, S.; Costea, M. Development of Thermodynamics with Finite Speed and Direct Method; Editura AGIR: Bucharest, Romania, 2011. [Google Scholar]
- Petrescu, S.; Harman, C.; Costea, M.; Feidt, M. Thermodynamics with finite speed versus thermodynamics in finite time in the optimization of Carnot cycle. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, Kohala, HI, USA, 16–20 March 2003.
- Petrescu, S.; Harman, C.; Bejan, A. The Carnot cycle with external and internal irreversibility. In Proceedings of the Florence World Energy Research Symposium, Energy for The 21st Century: Conversion, Utilization and Environmental Quality, Firenze, Italy, 6–8 July 1994.
- Petrescu, S.; Feidt, M.; Harman, C.; Costea, M. Optimization of the irreversible Carnot cycle engine for maximum efficiency and maximum power through use of finite speed thermodynamic analysis. In Proceedings of the 15th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, ECOS’2002, Berlin, Germany, 3–5 July 2002; Tsatsaronis, G., Moran, M., Cziesla, F., Bruckner, T., Eds.; Volume II, pp. 1361–1368.
- Petre, C.; Feidt, M.; Costea, M.; Petrescu, S. A model for study and optimization of real-operating refrigeration machines. Int. J. Energy Res. 2009, 33, 173–179. [Google Scholar] [CrossRef]
- Feidt, M. Energétique: Concepts et Applications; Dunod: Paris, France, 2006. [Google Scholar]
- Tondeur, D. Optimisation thermodynamique: Équipartition de production d'entropie. Available online: https://hal.archives-ouvertes.fr/hal-00560251/ (accessed on 25 June 2016).
- Tondeur, D. Optimisation thermodynamique. Equipartition: Exemples et applications. Available online: https://hal.archives-ouvertes.fr/hal-00560257/ (accessed on 25 June 2016).
- Dong, Y.; El-Bakkali, A.; Feidt, M.; Descombes, G.; Perilhon, C. Association of finite-time thermodynamics and a bond-graph approach for modelling an irreversible heat engine. Entropy 2012, 14, 1234–1258. [Google Scholar] [CrossRef]
- Ares de Parga, G.; Angulo-Brown, F.; Navarrete-González, T.D. A variational optimization of a finite-time thermal cycle with a nonlinear heat transfer law. Energy 1999, 24, 997–1008. [Google Scholar] [CrossRef]
- Ramírez-Moreno, M.A.; González-Hernández, S.; Angulo-Brown, F. The role of the Stefan–Boltzmann law in the thermodynamic optimization of an n-Müser engine. Phys. A Stat. Mech. Appl. 2016, 444, 914–921. [Google Scholar] [CrossRef]
- Qin, X.; Chen, L.; Sun, F.; Wu, C. Performance of an endoreversible four-heat-reservoir absorption heat pump with a generalized heat transfer law. Int. J. Therm. Sci. 2006, 45, 627–633. [Google Scholar] [CrossRef]
- Song, H.; Chen, L.; Sun, F. Endoreversible heat-engines for maximum power-output with fixed duration and radiative heat-transfer law. Appl. Energy 2007, 84, 374–388. [Google Scholar] [CrossRef]
- Petre, C. The use of Thermodynamics with Finite Speed to Study and Optimization of Carnot Cycle and Stirling Machines. Ph.D. Thesis, University Henri Poincaré of Nancy and University Politehnica of Bucharest, Bucharest, Romania, 2007. [Google Scholar]
- Dong, Y.; El-Bakkali, A.; Descombes, G.; Feidt, M.; Perilhon, C. Association of finite-time thermodynamics and a bond-graph approach for modelling an endoreversible heat engine. Entropy 2012, 14, 642–653. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M.; Petre, C.; Petrescu, S. Optimization of Direct Carnot Cycle. Appl. Therm. Eng. 2007, 27, 829–839. [Google Scholar] [CrossRef]
- Feidt, M.; Université de Lorraine, Nancy, France. Private communication, 2014.
- Haseli, Y. Performance of irreversible heat engines at minimum entropy generation. Appl. Math. Model. 2013, 37, 9810–9817. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Salamon, P.; Hoffmann, K.H.; Schubert, S.; Berry, R.S. Thermodynamics in finite time. IV: Minimum entropy production in heat engines. Phys. Rev. A 1980, 21, 2115–2129. [Google Scholar] [CrossRef]
- Johanessen, E.; Kjelstrup, S. Minimum entropy production rate in plug flow reactors: An optimal control problem solved for SO2 oxidation. Energy 2004, 29, 2403–2423. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feidt, M.; Costea, M.; Petrescu, S.; Stanciu, C. Nonlinear Thermodynamic Analysis and Optimization of a Carnot Engine Cycle. Entropy 2016, 18, 243. https://doi.org/10.3390/e18070243
Feidt M, Costea M, Petrescu S, Stanciu C. Nonlinear Thermodynamic Analysis and Optimization of a Carnot Engine Cycle. Entropy. 2016; 18(7):243. https://doi.org/10.3390/e18070243
Chicago/Turabian StyleFeidt, Michel, Monica Costea, Stoian Petrescu, and Camelia Stanciu. 2016. "Nonlinear Thermodynamic Analysis and Optimization of a Carnot Engine Cycle" Entropy 18, no. 7: 243. https://doi.org/10.3390/e18070243