Entropy-Weighted Instance Matching Between Different Sourcing Points of Interest
Abstract
:1. Introduction

2. Related Work
3. The Entropy-Weighted Approach for Finding Matched POIs
3.1. The Strategy of Attribute Selection
- (1)
- For an attribute category . If ( and ) or ( and ), then define the similarity of this attribute , and exclude this property in the weighted multi-attributes model.
- (2)
- If (), then confirm the calculation of according to the feature of attribute value and include this property in the weighted multi-attributes model.
3.2. Spatial Similarity

3.3. Name Similarity
3.4. Category Similarity


3.5. The Entropy-Weighted Multi-Attributes Method
- (1)
- Set the probability distribution of each calculation , i = 1, 2… n, j = 1, 2… m, where n refers to the count of discrete similarity that divided with unique interval, and m equal the amount of (for example, m = 5 in the Five-Methods Model).
- (2)
- Compute the normalized information entropy , the formula is given as follows [37]:where is the entropy constant and is the information entropy. In relation to = 0, the value of is defined as 0.
- (3)
- The weights are calculated as follows:
4. Case Study and Discussion
4.1. Experimental Dataset
4.2. The Spatial Attribute

4.3. The Name Attribute

4.4. The Category Attribute

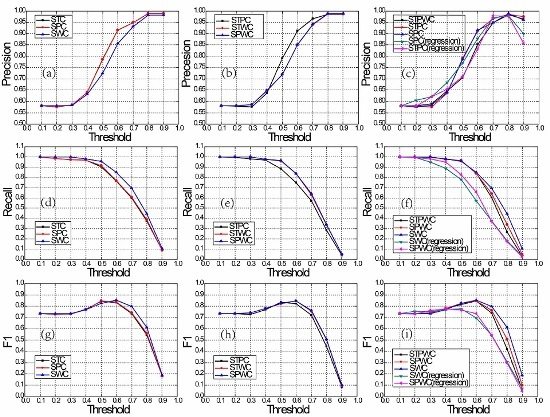
4.5. The Entropy-Weighted Multi-Attributes Model Analysis
| Similarity | P(1) | P(2) | P(3) | P(4) | P(5) |
|---|---|---|---|---|---|
| 0 ≤ s < 0.05 | 0 | 0 | 0 | 0 | 0.0830 |
| 0.05 ≤ s < 0.1 | 0.0040 | 0.0040 | 0.0040 | 0 | 0 |
| 0.1 ≤ s < 0.15 | 0.0079 | 0.0079 | 0.0040 | 0 | 0 |
| 0.15 ≤ s < 0.2 | 0.0356 | 0.0040 | 0 | 0 | 0.0040 |
| 0.2 ≤ s < 0.25 | 0.0395 | 0.0237 | 0.0198 | 0 | 0 |
| 0.25 ≤ s < 0.3 | 0.0237 | 0.0316 | 0.0356 | 0.004 | 0 |
| 0.3 ≤ s < 0.35 | 0.0514 | 0.0316 | 0.0277 | 0 | 0 |
| 0.35 ≤ s < 0.4 | 0.0277 | 0.0435 | 0.0356 | 0.004 | 0 |
| 0.4 ≤ s < 0.45 | 0.0198 | 0.0988 | 0.0791 | 0.0356 | 0.0079 |
| 0.45 ≤ s < 0.5 | 0.0395 | 0.0356 | 0.0514 | 0 | 0.0119 |
| 0.5 ≤ s < 0.55 | 0.0237 | 0.1067 | 0.0949 | 0.0514 | 0.0791 |
| 0.55 ≤ s < 0.6 | 0.0079 | 0.0632 | 0.0830 | 0.0277 | 0.0079 |
| 0.6 ≤ s < 0.65 | 0.0316 | 0.1067 | 0.0988 | 0.0395 | 0.0119 |
| 0.65 ≤ s < 0.7 | 0.0316 | 0.0870 | 0.0791 | 0.0909 | 0.0158 |
| 0.7 ≤ s < 0.75 | 0.0277 | 0.0909 | 0.0870 | 0.1067 | 0.0593 |
| 0.75 ≤ s < 0.8 | 0.0356 | 0.0909 | 0.0949 | 0.1581 | 0.1146 |
| 0.8 ≤ s < 0.85 | 0.0474 | 0.1107 | 0.1225 | 0.2055 | 0.1818 |
| 0.85 ≤ s < 0.9 | 0.0514 | 0.0237 | 0.0277 | 0.1502 | 0.1146 |
| 0.9 ≤ s < 0.95 | 0.1146 | 0.0119 | 0.0119 | 0.0632 | 0.1067 |
| 0.95 ≤ s < 1 | 0.3794 | 0 | 0 | 0 | 0.1462 |
| s = 1 | 0 | 0.0277 | 0.0435 | 0.0632 | 0.0553 |
| 0.765 | 0.873 | 0.872 | 0.739 | 0.766 |
| Abbreviation | Spatial | Text | Phonetic | WordSeg | Category | |
|---|---|---|---|---|---|---|
| Five-Methods Model | STPWC | 0.2386 | 0.1289 | 0.1299 | 0.2650 | 0.2376 |
| Four-Methods Model | STPC | 0.3246 | 0.1754 | 0.1768 | – | 0.3232 |
| STWC | 0.2742 | 0.1482 | – | 0.3046 | 0.2730 | |
| SPWC | 0.2739 | – | 0.1492 | 0.3042 | 0.2727 | |
| Three-Methods Model | STC | 0.3943 | 0.2131 | – | – | 0.3926 |
| SPC | 0.3936 | – | 0.2144 | – | 0.3920 | |
| SWC | 0.3219 | – | – | 0.3575 | 0.3205 |

5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hastings, J.T. Automated conflation of digital gazetteer data. Int. J. Geogr. Inf. Sci. 2008, 22, 1109–1127. [Google Scholar] [CrossRef]
- Porter, R.; Collins, L.; Powell, J.; Rivenburgh, R. Information space models for data integration, and entity resolution. Proc. SPIE 2012, 8396, 263–276. [Google Scholar]
- Ruiz, J.J.; Ariza, F.J.; Urena, M.A.; Blazquez, E.B. Digital map conflation: A review of the process and a proposal for classification. Int. J. Geogr. Inf. Sci. 2011, 25, 1439–1466. [Google Scholar] [CrossRef]
- Beeri, C.; Doytsher, Y.; Kanza, Y.; Safra, E.; Sagiv, Y. Finding Corresponding Objects when Integrating Several Geo-Spatial Datasets. In Proceedings of the 13th ACM International Workshop on Geographic Information Systems, Bremen, Germany, 4–5 November 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 87–96. [Google Scholar]
- Kitchin, R.M. Increasing the integrity of cognitive mapping research: Appraising conceptual schemata of environment behaviour interaction. Prog. Hum. Geogr. 1996, 20, 56–84. [Google Scholar] [CrossRef]
- Michalowski, M.; Ambite, J.L.; Thakkar, S.; Tuchinda, R.; Knoblock, C.A.; Minton, S. Retrieving and semantically integrating heterogeneous data from the web. IEEE Intell. Syst. 2004, 19, 72–79. [Google Scholar] [CrossRef]
- Safra, E.; Kanza, Y.; Sagiv, Y.; Beeri, C.; Doytsher, Y. Location-based algorithms for finding sets of corresponding objects over several geo-spatial data sets. Int. J. Geogr. Inf. Sci. 2010, 24, 69–106. [Google Scholar] [CrossRef]
- Fonseca, F.T.; Egenhofer, M.J.; Agouris, P.; Câmara, G. Using ontologies for integrated geographic information systems. Trans. GIS 2002, 6, 231–257. [Google Scholar] [CrossRef]
- Du, H.; Anand, S.; Alechina, N.; Morley, J.; Hart, G.; Leibovici, D.; Jackson, M.; Ware, M. Geospatial information integration for authoritative and crowd sourced road vector data. Trans. GIS 2012, 16, 455–476. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Li, B. A formal method for integrating distributed ontologies and reducing the redundant relations. Kybernetes 2009, 38, 1870–1879. [Google Scholar]
- Li, J.; He, Z.; Zhu, Q. An entropy-based weighted concept lattice for merging multi-source geo-ontologies. Entropy 2013, 15, 2303–2318. [Google Scholar] [CrossRef]
- Samal, A.; Seth, S.; Cueto, K. A feature-based approach to conflation of geospatial sources. Int. J. Geogr. Inf. Sci. 2004, 18, 459–489. [Google Scholar] [CrossRef]
- Garla, V.N.; Brandt, C. Semantic similarity in the biomedical domain: An evaluation across knowledge sources. BMC Bioinform. 2012, 13. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Morie, P.; Roth, D. Semantic integration in text: From ambiguous names to identifiable entities. AI Mag. 2005, 26, 45–58. [Google Scholar]
- Vasardani, M.; Winter, S.; Richter, K.F. Locating place names from place descriptions. Int. J. Geogr. Inf. Sci. 2013, 27, 2509–2532. [Google Scholar] [CrossRef]
- Wang, W.; Stewart, K. Spatiotemporal and semantic information extraction from web news reports about natural hazards. Comput. Environ. Urban Syst. 2015, 50, 30–40. [Google Scholar] [CrossRef]
- Mulliganni, C.; Janowicz, K.; Ye, M.; Lee, W.-C. Analyzing the spatial-semantic interaction of points of interest in volunteered geographic information. In Spatial Information Theory; Egenhofer, M., Giudice, N., Moratz, R., Worboys, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 350–370. [Google Scholar]
- Yang, B.S.; Zhang, Y.F.; Lu, F. Geometric-based approach for integrating vgi pois and road networks. Int. J. Geogr. Inf. Sci. 2014, 28, 126–147. [Google Scholar] [CrossRef]
- Safra, E.; Kanza, Y.; Sagiv, Y.; Doytsher, Y. Integrating Data from Maps on the World-Wide Web. In Web and Wireless Geographical Information Systems; Carswell, J.D., Tezuka, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 180–191. [Google Scholar]
- Scheffler, T.; Schirru, R.; Lehmann, P. Matching Points of Interest from Different Social Networking Sites. In KI 2012: Advances in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2012; pp. 245–248. [Google Scholar]
- McKenzie, G.; Janowicz, K.; Adams, B. A weighted multi-attribute method for matching user-generated points of interest. Cartogr. Geogr. Inf. Sci. 2014, 41, 125–137. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise shannon’s entropy and multi attribute decision making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Log-euclidean metrics for fast and simple calculus on diffusion tensors. Magn. Reson. Med. 2006, 56, 411–421. [Google Scholar] [CrossRef] [PubMed]
- Navarro, G. A guided tour to approximate string matching. ACM Comput. Surv. 2001, 33, 31–88. [Google Scholar] [CrossRef]
- Liu, W.; Cai, M.; Yuan, H.; Shi, X.; Zhang, W.; Liu, J. Phonotactic Language Recognition Based on Dnn-HMM Acoustic Model. In Proceedings of the 9th International Symposium on Chinese Spoken Language Processing (ISCSLP), Singapore, 12–14 September 2014; pp. 153–157.
- Meltzoff, A.N.; Kuhl, P.K.; Movellan, J.; Sejnowski, T.J. Foundations for a new science of learning. Science 2009, 325, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Mattys, S.L.; Davis, M.H.; Bradlow, A.R.; Scott, S.K. Speech recognition in adverse conditions: A review. Lang. Cognit. Process. 2012, 27, 953–978. [Google Scholar] [CrossRef]
- Nie, X.; Feng, W.; Wan, L.; Xie, L. Measuring Semantic Similarity by Contextual Word Connections in Chinese News Story Segmentation. In Proceddings of the 2013 IEEE International Conference on Acoustics, Speech And Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 8312–8316.
- Baidu. Available online: http://developer.baidu.com/map/index.php (accessed on 20 June 2015).
- Sina. Available online: http://open.weibo.com/ (accessed on 20 June 2015).
- Sehgal, V.; Getoor, L.; Viechnicki, P.D. Entity Resolution in Geospatial Data Integration. In Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, ACM-GIS’06, Arlington, VA, USA, 6–11 November 2006; Association for Computing Machinery: New York, NY, USA, 2006; pp. 83–90. [Google Scholar]
- Sanchez, D.; Batet, M. A semantic similarity method based on information content exploiting multiple ontologies. Expert Syst. Appl. 2013, 40, 1393–1399. [Google Scholar] [CrossRef]
- Liu, H.Z.; Bao, H.; Xu, D. Concept vector for semantic similarity and relatedness based on wordnet structure. J. Syst. Softw. 2012, 85, 370–381. [Google Scholar] [CrossRef]
- Dincer, I.; Cengel, Y. Energy, entropy and exergy concepts and their roles in thermal engineering. Entropy 2001, 3, 116–149. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Machado, J. Fractional order generalized information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xing, X.; Xia, H.; Huang, X. Entropy-Weighted Instance Matching Between Different Sourcing Points of Interest. Entropy 2016, 18, 45. https://doi.org/10.3390/e18020045
Li L, Xing X, Xia H, Huang X. Entropy-Weighted Instance Matching Between Different Sourcing Points of Interest. Entropy. 2016; 18(2):45. https://doi.org/10.3390/e18020045
Chicago/Turabian StyleLi, Lin, Xiaoyu Xing, Hui Xia, and Xiaoying Huang. 2016. "Entropy-Weighted Instance Matching Between Different Sourcing Points of Interest" Entropy 18, no. 2: 45. https://doi.org/10.3390/e18020045