1. Introduction
A fundamental thermodynamic theorem states that for whatever open process whose evolution can be approximated as a succession of quasi-equilibrium states and working in thermal contact with an ambient at
T0, the lost available power |
|,
i.e., the difference between the ideally produced or absorbed power and the one really extracted, is proportional to the global rate of entropy generation
:
[
1]. The lost power (
) is always positive, regardless of whether the system is a power producer (e.g., an expander) or a power user (e.g., a compressor). Although not often exploited in real design applications, this theorem is of the utmost importance for the designer, in that it allows for a direct comparison of different configurations (“design options”) that either produce the same output with less irreversible losses or use the same amount of resource input to generate a larger output; both cases corresponding of course to a higher resource-to-end use efficiency. Naturally, the minimization of the entropy generation is not an easy task in practical cases, especially when complicated boundary conditions apply and/or when the operating point is varying in time. During the last three decades the Entropy Generation Minimization (EGM) method has become a well-established procedure in thermal science and engineering. The method relies on the simultaneous application of the heat transfer and engineering thermodynamics principles, in pursuit of realistic models for heat transfer processes, devices and installations. The overwhelming majority of applications of the method for heat transfer problems employs lumped-sum parameter models: the global rate of entropy generation (
[W/K]) is analytically expressed as a function of the topology and physical characteristics of the system (critical dimension, materials...) using correlations for average heat transfer rates and fluid friction available in literature. Then, by varying one or more of the design variables which
depends upon, a minimum of the function
is sought after; thence, an optimal geometry is determined. Many examples of this lumped-sum parameter model technique applied to fundamental heat transfer problems are presented in [
1,
2,
3,
4,
5]. Pin-fins geometries are optimized with this method in [
6,
7], while plate-fins heat sinks are optimized in [
8,
9]. The key point of this
deterministic approach is the analytical definition of
as a function of critical design parameters, like geometry and working conditions. This function has to be inferred with the simultaneous application of principles of heat and mass transfer, fluid mechanics and engineering thermodynamics. Its ability to well describe the inherent irreversibility of the engineering system is closely linked to the “quality” of the correlations on which it relies. But, once we are able to actually write a semi-empirical analytic functional for
, finding its minimum is more a mathematical than a physical problem. One of the aims of the present work is to describe a different,
heuristic, approach: the initial configuration is successively improved by introducing design changes based on a careful analysis of the
local entropy generation maps obtained by means of Computational Fluid Dynamics (CFD) simulations. One of the advantages of this approach is that the rationale behind each step of the design process can be justified on a physical basis. This approach is particularly well suited for problems where a CFD simulation has to be carried out anyway (not explicitly for the purpose of a second-law analysis) and no reliable and explicit correlations for mean heat transfer and fluid friction are available. Typical examples are turbomachinery and (convective) heat exchangers design problems. While this approach has been already adopted in some turbomachinery problems (see [
10,
11]), examples for heat exchangers like the one covered in this work appear quite rarely in the archival literature. This approach consists in focusing the attention first on the local entropy generation rates
,
and in considering the global one
only after having carefully studied the implications of the local irreversibility on the overall design. It must be noted that, while
cannot
directly reflect the specific local features of the flow that are necessary for its phenomenological interpretation, it is nevertheless, the global quantifier that allows us to identify which one of two different configurations is the better performer from a second-law perspective: if systems A and B have the same input and operate so that
, it can be inferred that system A operates more irreversibly than system B, therefore -ceteris paribus- B should be preferred. In order to calculate these local rates, both the velocity and temperature field have to be completely resolved, and therefore a CFD solver,
i.e., a distributed-parameter model, is needed. Once the entropy rates are known, thanks to the visualization tool of the solver, we can display the maps of
and
, so that the designer is able to literally see where the entropy is produced at a higher rate and therefore where exergy is destroyed at a higher rate; it is possible to pinpoint the areas where we should focus our attention on.
2. The LED Spotlight
Eighteen diodes are printed on a fibreglass plate to form a LED spotlight whose layout and dimensions are shown in
Figure 1 and
Figure 2. Every diode dissipates 3 W and the maximum allowed temperature of the plate (and of the base of each diode) is 80 °C. In addition, the temperature difference between the diodes should not exceed 10 °C. In order to level out the temperatures of the diodes, a so called “thermal pad”, consisting of a 70 µm thick copper film, is placed under the plate.
Figure 1.
The diode spotlight.
Figure 1.
The diode spotlight.
The cooling relies on the forced convection driven by a jet of air impinging on the thermal pad that lies on the bottom of the fibreglass plate shown in
Figure 1. In order to assess the temperature field in the absence of heat transfer augmentation surfaces, the simple geometry S-1 is designed and simulated. Taking advantage of the symmetries of the geometry, only a 90° portion of the spotlight is modelled. This geometry consists of the copper plate only, cooled by the impinging air (see
Figure 3). The inlet mass flow is determined assuming an increase of the air temperature of
:
At steady-state, the average temperature of the base is approximately 250 °C, which is unacceptable. Therefore, several complex geometries of aluminium fins for heat transfer augmentation are designed and simulated. A pseudo-optimization process is carried out via a successive series of design modifications based on a careful analysis of the local entropy generation maps. The design modifications concern mostly the fin spacing and dimensions.
Figure 2.
Planar view of the spotlight. The diodes (heat sources) are indicated by red circles. Only the blue sector is modelled in this study.
Figure 2.
Planar view of the spotlight. The diodes (heat sources) are indicated by red circles. Only the blue sector is modelled in this study.
3. Alternative Geometries
Geometry S-2 features periodically spaced in the radial direction aluminium plate-fins 0.75 mm thick, 12 mm high and 12 mm long. Since the external diodes are equally spaced at 30° and the internal ones at 60°, it is decided to place one fin every 15° for a total of 24 fins (six per quadrant), so that each diode is “covered” by one plate-fin. As shown in
Figure 4, the domain has been slightly modified. In order to ensure structural stability of the fins (the fluid enters the domain with v
inlet ≈ 20 m/s) two physical walls have been added. The heat sources are modelled as rectangles for ease of mesh generation.
In order to further improve heat transfer and lower the average temperature of the diodes, geometry S-3 is designed and simulated (
Figure 5). Geometry S-3 features 12 additional shorter fins placed where the diodes are denser and the heat flux is maximum (see
Figure 6).
Figure 6.
Bottom view of geometry S-3.
Figure 6.
Bottom view of geometry S-3.
In geometry S-3, the interstitial fins are shorter than the others. To simplify the geometry from a technological point of view, and augment the heat transfer area, geometry S-3-1 was designed (
Figure 7a). For reasons that will be clear later, geometry S-3-1 is simply obtained by cutting the top external corner of the fins at z = 7 mm and r = 8 mm (
Figure 7b). A complete cut at z = 7 mm is done for the other two geometries, S-3-3 in
Figure 7c, and S-3-4 in
Figure 7d. Both feature fins 7 mm high, but the former has shorter interstitial fins.
Figure 7.
(a) Geometry S-3-1. (b) Geometry S-3-2. (c) Geometry S-3-3. (d) Geometry S-3-4.
Figure 7.
(a) Geometry S-3-1. (b) Geometry S-3-2. (c) Geometry S-3-3. (d) Geometry S-3-4.
3.1. Strategy for Probing the Solution Space and Description of the Heuristic Procedure
The entropy generation rate can be shown, for the case in study (
i.e., in the absence of phase changes and chemical reactions), to consist of two parts [
2]: one, called “
viscous” (
), that depends on the physical viscosity, on the local temperature of the fluid and on the square of the local variation of the velocity (velocity gradient), and another, called “
thermal” (
), that depends on the physical conductivity, on the square of the local temperature of the fluid and on the square of local temperature gradient:
where
ϕ is the rate of
viscous dissipation per unit volume. Note that the entropy generation rate expressed in (2) is per unit volume (W/(K m
3)). The global entropy generation rate
of the entire domain (W/K) is computed simply as the integral of the local rates over the entire volume V:
As mentioned above, the approach adopted in this work consists in focusing the attention first on the local entropy generation rates
,
and in considering the global one
only after having carefully studied the implications of the local irreversible losses. In particular, the procedure for ‘optimising’ a design by means of an entropy generation analysis is the following:
Define a starting geometry or a family of starting geometries.
Acquire the geometries and create the computational grid to be imported into the CFD solver.
Compute the temperature and the velocity fields.
Compute and display the maps of , .
Integrate local values to obtain the global entropy generation rate .
Modify the design as suggested by a critical inspection of the local entropy maps.
Repeat the computation, and iterate until a feasible and acceptable “minimum” of is obtained.
It is now clear that the process described above is not a proper optimization, but rather a heuristic design approach, essentially based on a thermodynamically sound trial-and-error procedure. Nevertheless, the amount of phenomenological information contained in the local entropy generation maps is so high that a convergence towards a better design is almost guaranteed [
10].
5. Results and Discussion
The simulation results of geometry S-2 are given in
Table 1. The two sources of entropy are of the same order of magnitude. As shown in
Figure 10, close to the outlet only the lower part of the fins is invested by the impinging jet.
Table 1.
Simulation results for geometry all geometries. Tav,diodes is the average temperature of the diodes; ∆Tdiodes is the maximum temperature difference between the diodes.
Table 1.
Simulation results for geometry all geometries. Tav,diodes is the average temperature of the diodes; ∆Tdiodes is the maximum temperature difference between the diodes.
| Geometry | Tav,diodes, °C | ∆Tdiodes | , W/K | , W/K | , W/K |
|---|
| S-2 | 67.5 | 3 | 5.19E-03 | 1.74E-03 | 6.92E-03 |
| S-3 | 56.5 | 3 | 3.85E-03 | 2.89E-03 | 6.47E-03 |
| S-3.1 | 55.4 | 4 | 3.71E-03 | 2.90E-03 | 6.62E-03 |
| S-3.2 | 55.8 | 4 | 3.83E-03 | 2.83E-03 | 6.66E-03 |
| S-3.3 | 70.0 | 4 | 5.38E-03 | 1.13E-03 | 6.51E-03 |
| S-3.4 | 68.4 | 4 | 5.46E-03 | 1.16E-03 | 6.62E-03 |
Figure 10.
Streamlines for the cooling arrangement S-2.
Figure 10.
Streamlines for the cooling arrangement S-2.
This causes a back flow in the upper and more external zone of the outlet where, however, the fluid has almost zero velocity: the fins are almost isolated being surrounded by a basically stagnant gas.
Figure 11 shows the contours of temperatures in selected sections. The thermal boundary layers are clearly visible; they are very thin due the high velocities and very short characteristic length and they merge only very close to the baseplate due to its influence. In between the fins the flow is almost undisturbed.
Figure 11.
Contours of temperature for geometry S-2 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 11.
Contours of temperature for geometry S-2 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 12 shows the distribution of the thermal entropy generation scaled by the total entropy generation rate (
Be, Bejan number). Again, the influence of the boundary layer, both thermal and mechanical, is clearly visible.
has a stronger influence close to the baseplate and in the stagnation zone, where the velocities are lower. In addition, almost only
is produced in the upper external zone of the fins where, as mentioned above, the fins are exchanging heat with an almost stagnant fluid. On the contrary,
is predominant in between the fins and in the wakes. A high
zone is present at the interface of the high velocity entering flow with the ambient (coming from the outlet) flow, as can be seen also in
Figure 13.
Figure 12.
Contours of the Bejan number Be for geometry S-2 at z = 2 mm and z = 8 mm.
Figure 12.
Contours of the Bejan number Be for geometry S-2 at z = 2 mm and z = 8 mm.
Figure 13.
Contours of for geometry S-2 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 13.
Contours of for geometry S-2 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 14.
Contours of for geometry S-2 at z = 2 mm and r = 7 mm.
Figure 14.
Contours of for geometry S-2 at z = 2 mm and r = 7 mm.
As stated before Geometry S-3 features 12 additional shorter fins placed where the diodes are more densely packed and the heat flux is maximum (see
Figure 6). Even with the insertion of additional fins, the boundary layers merge only near the baseplate (
Figure 15).
Figure 15.
Contours of temperature for geometry S-3 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 15.
Contours of temperature for geometry S-3 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Nevertheless, since the boundary layers are close to each other, in these zones
reaches lower values than for geometry S-2 (see
Figure 14 and
Figure 16) and over the whole volume the thermal entropy generation rate drops of about 26% (
Table 1).
Figure 16.
Contours of for geometry S-3 at z = 2 mm, r = 7 mm.
Figure 16.
Contours of for geometry S-3 at z = 2 mm, r = 7 mm.
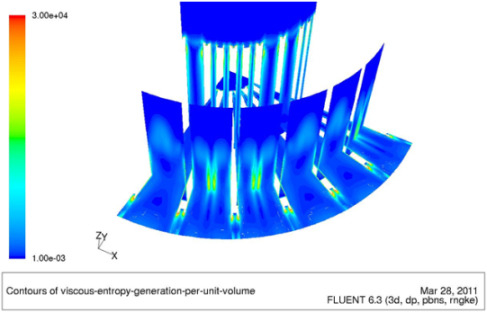
However, the presence of the added fins causes also an increase of about 67% in the viscous entropy generation. In fact, new vortices appear at the external end of the fins where the vorticity,
and the turbulent kinetic energy k all reach their peak values. The presence of the added fins, in fact, causes a local increment of the pressure whose effects propagates upstream; therefore, the mass flow is no longer evenly distributed between the channels bounded by the fins but attains lower values where the inter-fin spacing are lower. Higher velocities lead to high viscous dissipation in the larger channels (
Figure 17).
Figure 17.
Contours of for geometry S-3 at z = 2 mm, r = 7 mm and r = 12.5 mm.
Figure 17.
Contours of for geometry S-3 at z = 2 mm, r = 7 mm and r = 12.5 mm.
In conclusion, is almost the same in both geometries, even though the relative contributions of the two portions and are completely different. In particular, the noticeable difference between the thermal entropy generation rate is reflected by the difference of the average temperatures of the diodes: Tav,diodes is 56.5 °C and 67.5 °C in geometry S-3 and S-2, respectively.
In geometry S-3, the interstitial fins have been designed shorter than the others. However, as can be seen in
Figure 15, the thermal wake behind the shorter fins does not merge the thermal boundary layers of the longer fins due to the relatively cold and almost undisturbed stream coming from the inlet at high velocity; this stream quickly absorbs the wake. Therefore to simplify the geometry from a technological point of view, and augment the heat transfer area, geometry S-3-1 was designed (
Figure 7a). Looking at
Table 1, it can be seen that no appreciable differences are found in the entropy rates (less than 5% difference) while the
Tav,diodes is one degree lower.
As for geometry S-2, the same behaviour in the upper and more external zone of the volume exists for S-3 and S-3-1. In these areas, the fins are almost isolated, are surrounded by a gas basically stagnant, and therefore are ineffective. For this reasons geometries S-3-2, S-3-3, and S-3.4 were designed. While S-3.2 has the lowest thermal entropy rate (and lower average temperature of the diodes), the other two produce a considerably smaller
but their lower heat transfer area leads to higher temperatures. As shown in
Figure 18, the global production of entropy for all the S geometries is almost the same (the maximum difference is less than 6%), therefore from a thermodynamic perspective they perform equally. The discriminating factor is, though, the difference in their respective average temperatures. Since the characteristic velocities are comparable, the heat transfer coefficients are practically constant for all three configurations; therefore, the heat transfer is, with a good degree of approximation, directly proportional to the heat transfer area. In this perspective the best geometries are S-3, S-3-1 and S-3-2. It should be mentioned that the colour of the light shed by the diodes depends on their temperature, which for the purposes of this particular application should not exceed ≈80 °C. When one of the former geometries has been chosen, there are two ways to vary this temperature: to augment the voltage under which the diodes operate or to decrease the inlet air mass flow rate. The temperatures of the diodes in the geometries with less heat transfer area would be more sensible to the variations of the inlet mass flow.
Figure 18.
Global entropy production rate and average temperature of the diodes Tav,diodes for all S geometries.
Figure 18.
Global entropy production rate and average temperature of the diodes Tav,diodes for all S geometries.
5.1. Required Fan Power and Final Comparisons
The specific work per unit time that the fan has to deliver to the fluid can be calculated as:
where:
The results for all the S geometries are given in
Table 2. As expected, the geometries which features the highest heat transfer area are also the most power demanding ones.
Table 2.
Required fan power for the indicated geometries.
Table 2.
Required fan power for the indicated geometries.
| Geometry | m, kg/s | ρ, kg/m3 | ∆ptot, Pa | P, W |
|---|
| S-2 | 0.010731 | 1.2 | 501 | 4.5 |
| S-3 | 0.010731 | 1.2 | 814 | 7.3 |
| S-3.1 | 0.010731 | 1.2 | 789 | 7.1 |
| S-3.2 | 0.010731 | 1.2 | 786 | 7.0 |
| S-3.3 | 0.010731 | 1.2 | 295 | 2.6 |
| S-3.4 | 0.010731 | 1.2 | 297 | 2.7 |
A typical CPU dissipates around 35–50 W and the cooling usually relies on 90 × 90 × 70 mm aluminum plate-fin heat sinks, with a 80 mm fan on top. Such a fan usually produces 50 m3/h ≈ 0.017 kg/s, which means that air enters the heat sink with an average velocity of ≈3 m/s. As stated above, the spotlight has very small dimensions: therefore, even if the mass flow and the temperature field are comparable, the needed average inlet velocity is much higher, as it is the required fan power. However, radially placed fins provide higher heat transfer coefficients and employ less material even though their fabrication process is more complicated.
5.2. Conclusions
The thermodynamic fields, in all simulations, have been evaluated on a grid satisfactorily refined, using the total entropy generation rate as an objective function. In this way, a sufficiently large and reliable database of “experiments” has been obtained. The pseudo-optimization process in this work has proved to be an effective tool in the hands of a designer: in fact, a significant improvement of the thermodynamic performance has been obtained. The adopted procedure for “optimizing” a design by means of an entropy generation analysis is not an optimization proper, but rather a heuristic design approach, essentially based on a thermodynamically sound trial-and-error procedure. It results from the direct scanning of a finite (and in general quite small) solution set and is more similar to a (single or multiple parameter) sensitivity study. Nevertheless, the amount of phenomenological information contained in the local entropy generation maps is so high and detailed that a better design can always be defined. In this specific case, it was found that the best performance is attained when the fins are periodically spaced in the radial direction. In particular, all six geometries S-2, S-3, S-3-1, S-3-2, S-3-3 and S-3-4 can effectively cool the array of diodes while keeping the base-plate temperature well below 80 °C. Even though the global entropy production rate varies relatively very little between the configurations, big differences are found in the numerical values of the two sources of entropy and . These differences are reflected in the average temperature of the diodes and in the required fan power: the lower , the lower Tav,diodes; the higher , the higher the required fan power.