Freezing of Solute-Laden Aqueous Solutions: Kinetics of Crystallization and Heat- and Mass-Transfer-Limited Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Aqueous Solutions: Biological Media
2.2. Differential Scanning Calorimeter (DSC) Experiments
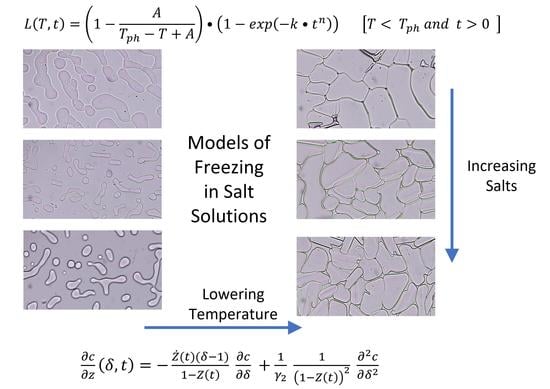
2.3. Temperature (T) and Time (t) Dependence of Latent Heat Release, L (T,t): Avrami-Like Model of Crystallization
2.4. Heat- and Mass-Transfer-Limited Model of Freezing of a Salt Solution in a Small Container
2.5. Numerical Scheme
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Devireddy, R.V.; Leo, P.H.; Lowengrub, J.S.; Bischof, J.C. Measurement and Numerical Analysis of Freezing in Solutions Enclosed in a Small Container. Int. J. Heat Mass Transf. 2002, 45, 1915–1931. [Google Scholar] [CrossRef] [Green Version]
- Hayes, L.J.; Diller, K.R.; Chang, H.J. A Robust Numerical Method for Latent Heat Release During Phase Change. ASME-HTD 1986, 62, 63–69. [Google Scholar]
- Avrami, M. Kinetics of Phase Change I. General Theory. J. Chem. Phys. 1939, 7, 1103–1121. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Pergamon Press: London, UK, 1981; pp. 540–545. ISBN 978-0-08-044019-4. [Google Scholar]
- Moran, T. The Freezing of Gelatine Gel. Proc. R. Soc. 1926, 112, 30–46. [Google Scholar]
- Cooke, R.; Kuntz, I.D. The Properties of Water in Biological Systems. Ann. Rev. Biophys. Bioeng. 1974, 3, 95–126. [Google Scholar] [CrossRef]
- Fennema, O.R.; Powrie, W.D.; Marth, E.H. Low-Temperature Preservation of Foods and Living Matter; Marcel Dekker Inc.: New York, NY, USA, 1973; pp. 63–66. ISBN 978-0-82-471185-6. [Google Scholar]
- Williams, R.J.; Meryman, H.T. A Calorimetric Method for Measuring Ice in Frozen Solutions. Cryobiology 1965, 1, 317–323. [Google Scholar] [CrossRef]
- Boutron, P. More Accurate Determination of the Quantity of Ice Crystallized at Low Cooling Rates in the Glycerol and 1,2-Propanediol Aqueous Aolutions: Comparison with Equilibrium. Cryobiology 1984, 21, 183–191. [Google Scholar] [CrossRef]
- Boutron, P. Comparison with the Theory of the Kinetics and Extent of Ice Crystallization and of the Glass-Forming Tendency in Aqueous Cryoprotective Solutions. Cryobiology 1986, 23, 88–102. [Google Scholar] [CrossRef]
- Hey, J.M.; MacFarlane, D.R. Crystallization of Ice in Aqueous Solutions of Glycerol and Dimethylsulfoxide. Cryobiology 1996, 33, 205–216. [Google Scholar] [CrossRef]
- Iijima, T. Thermal Analysis of Cryoprotective Solutions for Red Blood Cells. Cryobiology 1998, 36, 165–173. [Google Scholar] [CrossRef]
- He, X. Thermostability of Biological Systems: Fundamentals, Challenges and Quantification. Open Biomed. Eng. J. 2011, 5, 47–73. [Google Scholar] [CrossRef]
- Bruyere, P.; Baudot, A.; Joly, T.; Commin, L.; Pillet, E.; Guerin, P.; Louis, G.; Josson-Schramme, A.; Buff, S. A Chemically Deifned Medium for Rabbit Embryo Cryopreservation. PLoS ONE 2013, 8, e71547. [Google Scholar] [CrossRef]
- Lorinczy, D.; Fazekas, G. DSC Analysis of Cryopreservation on the Structure of Porcine Aortic Biograft as a Function of Storage Time. J. Therm. Anal. Calorim. 2022, 147, 10411–10417 . [Google Scholar] [CrossRef]
- Simatos, D.; Faure, M.; Bonjour, E.; Couach, M. The Physical State of Water at Low Temperatures in Plasma with Different Water Contents as Studied by Differential Thermal Analysis and Differential Scanning Calorimetry. Cryobiology 1975, 12, 202–208. [Google Scholar] [CrossRef]
- Rahman, M.S.; Al-Saidi, G.; Guizani, N.; Abdullah, A. Development of State Diagram of Bovine Gelatine by Measuring Thermal Characteristics using Differential Scanning Calorimetry (DSC) and Cooling Curve Method. Thermochim. Acta 2010, 509, 111–119. [Google Scholar] [CrossRef]
- Ross, K.D. Differential Scanning Calorimetry of Nonfreezable Water in solute Macromolecule-Water Systems. J. Food Sci. 1978, 43, 1812–1815. [Google Scholar] [CrossRef]
- Gekko, K.; Satake, I. Differential Scanning Calorimetry of Unfreezable Water in Water-Protein-Polyol Systems. Agric. Biol. Chem. 1981, 45, 2209–2217. [Google Scholar]
- Schenz, T.W.; Israel, B.; Rosolen, M.A. Thermal Analysis of Water-Containing Systems. In Water Relationships in Food; Levine, H., Slade, L., Eds.; Plenum Press: New York, NY, USA, 1991; pp. 199–214. [Google Scholar]
- Demetzos, C. Differential Scanning Calorimetry (DSC): A Tool to Study the Thermal Behavior of Lipid Bilayers and Liposomal Stability. J. Liposome Res. 2008, 18, 159–173. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.F. Measurement of Bound Water Content in Sludge: The Use of Differential Scanning Calorimetry (DSC). J. Chem. Technol. Biotechnol. 1995, 62, 359–365. [Google Scholar] [CrossRef]
- Murase, N.; Franks, F. Salt Precipitation During the Freeze-Concentration of Phosphate Buffer Solutions. Biophys. Chem. 1989, 34, 293–300. [Google Scholar] [CrossRef]
- Chang, Z.; Hansen, T.N.; Baust, J.G. The Effect of Antifreeze Proteins on the Devitrification of a Cryoprotective System. Cryo-Letters 1991, 12, 215–226. [Google Scholar]
- Dolev, M.B.; Braslavsky, I.; Davies, P.L. Ice-Binding Proteins and Their Function. Ann. Rev. Biochem. 2016, 85, 515–542. [Google Scholar] [CrossRef] [PubMed]
- Staszczuk, P. Novel Studies of Phase and Structural Transitions in Bulk and Vicinal Water. Colloids Surf. A Physicochem. Eng. Asp. 1995, 94, 213–224. [Google Scholar] [CrossRef]
- Rasmussen, D.H.; Macaulay, M.N.; Mackenzie, A.P. Supercooling and Nucleation of Ice in Single Cells. Cryobiology 1975, 12, 328–339. [Google Scholar] [CrossRef]
- Franks, F.; Mathias, S.F.; Galfre, P.; Webster, S.D.; Brown, D. Ice Nucleation and Freezing in Undercooled Cells. Cryobiology 1983, 20, 298–309. [Google Scholar] [CrossRef]
- Franks, F.; Bray, M. Mechanism of Ice Nucleation in Undercooled Plant Cells. Cryo-Letters 1980, 1, 221–226. [Google Scholar]
- Bryant, G. DSC Measurements of Cell Suspensions During Successive Freezing Runs: Implications for the Mechanisms of Intracellular Ice Formation. Cryobiology 1995, 32, 114–128. [Google Scholar] [CrossRef]
- Ramlov, H.; Hvidt, A. Artemia Cysts at Subzero Temperatures Studied by Differential Scanning Calorimetry. Cryobiology 1992, 29, 131–137. [Google Scholar] [CrossRef]
- Myers, S.P.; Pitt, R.E.; Lynch, D.V.; Steponkus, P.L. Characterization of Intracellular Ice Formation in Drosophila Melanogaster Embryos. Cryobiology 1989, 26, 472–484. [Google Scholar] [CrossRef]
- Körber, C.H.; Englich, S.; Rau, G. Intracellular Ice Formation: Cryomicroscopical Observation and Calorimetric Measurement. J. Microsc. 1991, 161, 313–325. [Google Scholar] [CrossRef]
- Han, B.; Bischof, J.C. Thermodynamic Nonequilibrium Phase Change Behavior and Thermal Properties of Biological Solutions for Cryobiological Applications. ASME J. Biomech. Eng. 2004, 126, 196–203. [Google Scholar] [CrossRef] [PubMed]
- Devireddy, R.V.; Raha, D.; Bischof, J.C. Measurement of Water Transport During Freezing in Cell Suspensions Using a Differential Scanning Calorimeter. Cryobiology 1998, 36, 124–155. [Google Scholar] [CrossRef] [PubMed]
- Devireddy, R.V.; Swanlund, D.J.; Roberts, K.P.; Bischof, J.C. Sub-zero Water Permeability Parameters of Mouse Spermatozoa in the Presence of Extracellular Ice and Cryoprotective Agents. Biol. Reprod. 1999, 61, 764–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Devireddy, R.V.; Swanlund, D.J.; Roberts, K.P.; Pryor, J.L.; Bischof, J.C. The Effect of Extracellular Ice and Cryoprotective Agents on the Water Permeability Parameters of Human Sperm Plasma Membrane During Freezing. Hum. Reprod. 2000, 15, 1125–1135. [Google Scholar] [CrossRef] [Green Version]
- Devireddy, R.V.; Swanlund, D.J.; Alghamdi, A.S.; Duoos, L.A.; Troedsson, M.H.T.; Bischof, J.C.; Roberts, K.P. Measured Effect of Collection and Cooling Conditions on the Motility and the Water Transport Parameters at Subzero Temperatures of Equine Spermatozoa. Reproduction 2002, 124, 643–648. [Google Scholar] [CrossRef]
- Devireddy, R.V.; Olin, T.; Swanlund, D.J.; Vincente, W.; Troedsson, M.H.T.; Bischof, J.C.; Roberts, K.P. Cryopreservation of Equine Spermatozoa: Optimal Cooling Rates in the Presence and Absence of Cryoprotective Agents. Biol. Reprod. 2002, 66, 222–231. [Google Scholar] [CrossRef] [Green Version]
- Thirumala, S.; Ferrer, M.S.; Al-Jarrah, A.; Eilts, B.E.; Paccamonti, D.L.; Devireddy, R.V. Cryopreservation of Canine Spermatozoa: Theoretical Prediction of Optimal Cooling Rates in the Presence and Absence of Cryoprotective Agents. Cryobiology 2003, 47, 109–124. [Google Scholar] [CrossRef]
- He, Y.; Dong, Q.; Tiersch, T.R.; Devireddy, R.V. Variation in the Membrane Transport Properties and Predicted Optimal Rates of Freezing for Spermatozoa of Diploid and Tetraploid Pacific Oyster Crassostrea Gigas. Biol. Reprod. 2004, 70, 1428–1437. [Google Scholar] [CrossRef] [Green Version]
- Devireddy, R.V.; Fahrig, B.; Godke, R.A.; Leibo, S.P. Subzero Water Transport Characteristics of Boar Spermatozoa Confirm Observed Optimal Cooling Rates. Mol. Reprod. Dev. 2004, 67, 446–457. [Google Scholar] [CrossRef] [PubMed]
- Thirumala, S.; Dong, Q.; Tiersch, T.R.; Devireddy, R.V. A Theoretically Estimated Optimal Cooling Rate for the Cryopreservation of Sperm Cells From A Live-bearing Fish, The Green Swordtail Xiphophorus helleri. Theriogenology 2005, 63, 2395–2415. [Google Scholar] [CrossRef] [Green Version]
- Thirumala, S.; Gimble, J.M.; Devireddy, R.V. Transport Phenomena During Freezing of Adipose Tissue Derived Adult Stem Cells. Biotech. Bioeng. 2005, 92, 372–383. [Google Scholar] [CrossRef]
- Pinisetty, D.; Dong, Q.; Tiersch, T.R.; Devireddy, R.V. Subzero Water Permeability Parameters and Optimal Freezing Rates for Sperm Cells of the Southern Platyfish, Xiphophorus maculatus. Cryobiology 2005, 50, 250–263. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Saenz, J.; Godke, R.A.; Devireddy, R.V. Effect of Cholesterol-Loaded Cyclodextrin on Freezing Induced Water Loss in Bovine Sperm. Reproduction 2006, 131, 875–886. [Google Scholar] [CrossRef] [Green Version]
- Thirumala, S.; Campbell, W.T.; Vicknair, M.R.; Tiersch, T.R.; Devireddy, R.V. Freezing Response and Optimal Cooling Rates for Cryopreserving Sperm Cells of Striped Bass, Morone saxatilis. Theriogenology 2006, 66, 964–973. [Google Scholar] [CrossRef] [PubMed]
- Devireddy, R.V.; Campbell, W.T.; Buchanan, J.T.; Tiersch, T.R. Freezing Response of White Bass (Morone chrysops) Sperm Cells. Cryobiology 2006, 52, 440–445. [Google Scholar] [CrossRef]
- Thirumala, S.; Forman, J.M.; Monroe, W.T.; Devireddy, R.V. Freezing and Post-thaw Apoptotic Behavior of Cells in the Presence of Palmitoyl Nanogold Particles. Nanotechnology 2007, 18, 19. [Google Scholar] [CrossRef]
- Alapati, R.; Stout, M.; Saenz, J.; Gentry, G.T., Jr.; Godke, R.A.; Devireddy, R.V. Comparison of the Permeability Properties and Post-Thaw Motility of Ejaculated and Epididymal Bovine Spermatozoa. Cryobiology 2009, 59, 700–706. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, M.; Choi, J.-H.; Devireddy, R.V.; Roberts, K.P.; Wolkers, W.F.; Makhlouf, A.; Bischof, J.C. Cellular Biophysics During Freezing of Rat and Mouse Sperm Predicts Post-Thaw Motility. Biol. Reprod. 2009, 81, 700–706. [Google Scholar] [CrossRef] [Green Version]
- Mori, S.; Choi, J.-H.; Devireddy, R.V.; Bischof, J.C. Calorimetric Measurement of Water Transport and Intracellular Ice Formation During Freezing in Cell Suspension. Cryobiology 2012, 65, 242–255. [Google Scholar] [CrossRef]
- Devireddy, R.V.; Bischof, J.C. Measurement of Water Transport During Freezing in Mammalian Liver Tissue–Part II: The Use of Differential Scanning Calorimetry. ASME J. Biomech. Eng. 1998, 120, 559–569. [Google Scholar] [CrossRef] [PubMed]
- Devireddy, R.V.; Smith, D.J.; Bischof, J.C. Mass Transfer During Freezing of Rat Prostate Tumor Tissue. AIChE J. 1999, 45, 639–653. [Google Scholar] [CrossRef]
- Devireddy, R.V.; Barratt, P.R.; Storey, K.B.; Bischof, J.C. Liver Freezing Response of the Freeze Tolerant Wood Frog, Rana Sylvatica, in the Presence and Absence of Glucose. I. Experimental Measurements. Cryobiology 1999, 38, 310–326. [Google Scholar] [CrossRef]
- Devireddy, R.V.; Li, G.; Leibo, S.P. Suprazero Cooling Conditions Significantly Influence Subzero Permeability Parameters of Mammalian Ovarian Tissue. Mol. Reprod. Dev. 2006, 73, 330–341. [Google Scholar] [CrossRef]
- Kardak, A.; Leibo, S.P.; Devireddy, R.V. Freezing Response of Equine and Macaque Ovarian Tissue in Mixtures of Dimethylsulfoxide and Ethylene Glycol. ASME J. Biomech. Eng. 2007, 129, 688–694. [Google Scholar] [CrossRef]
- Li, G.; Thirumala, S.; Leibo, S.P.; Devireddy, R.V. Subzero Water Transport Characteristics and Optimal Rates of Freezing Macaca mulatta (Rhesus Monkey) Ovarian Tissue. Mol. Reprod. Dev. 2006, 73, 1600–1611. [Google Scholar] [CrossRef] [PubMed]
- Devireddy, R.V. Cryobiology of Ovarian Tissues: Known Knowns and Known Unknowns. Minerva Ginecol. 2018, 70, 387–401. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change II. Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change III. Granulation, Phase Change and Microstructure. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Guttman, C.M.; Flynn, J.H. On the Drawing of the Baseline for Differential Scanning Calorimetric Calculation of Heats of Transition. Anal. Chem. 1973, 45, 408–411. [Google Scholar] [CrossRef]
- Bronshteyn, V.L.; Steponkus, P.L. Calorimetric Studies of Freeze-Induced Dehydration of Phospholipids. Biophys. J. 1993, 65, 1853–1865. [Google Scholar] [CrossRef] [Green Version]
- McNaughton, J.L.; Mortimer, C.T. Differential Scanning Calorimetry; The Perkin-Elmer Corporation: Norwalk, CT, USA, 1975; Volume 10, pp. 2–41. [Google Scholar]
- Bershtein, V.A.; Egorov, V.M. Differential Scanning Calorimetry of Polymers: Physics, Chemistry, Analysis, Technology; Kemp, T.J., Ed.; Ellis Horwood: New York, NY, USA, 1994; ISBN 978-0-13-218215-7. [Google Scholar]
- Devireddy, R.V.; Smith, D.J.; Bischof, J.C. Effect of Microscale Mass Transport and Phase Change on Numerical Prediction of Freezing in Biological Tissues. ASME J. Heat Trans. 2002, 124, 365–374. [Google Scholar] [CrossRef]
- Kubota, N.; Mullin, J.W. A Kinetic Model for Crystal Growth from Aqueous Solution in the Presence of Impurity. J. Cryst. Growth 1995, 152, 203–208. [Google Scholar] [CrossRef]
- Long, Y.; Shanks, R.A.; Stachurski, Z.H. Kinetics of Polymer Crystallization. Prog. Polym. Sci. 1995, 20, 651–701. [Google Scholar] [CrossRef]
- MacFarlane, D.R.; Forsyth, M.; Barton, C.A. Vitrification and Devitrification in Cryopreservation, in: Advances in Low-Temperature Biology; Steponkus, P.L., Ed.; JAI Press LTD: London, UK, 1992; Volume 1, pp. 221–278. [Google Scholar]
- Cahn, J.W. The Kinetics of Grain Boundary Nucleated Reactions. Acta Metall. 1956, 4, 49–459. [Google Scholar] [CrossRef]
- Cahn, J.W. Transformation Kinetics during Continuous Cooling. Acta Metall. 1956, 4, 572–575. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetics of Non-Isothermal Crystallization. Polymer 1971, 12, 150–158. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 2nd ed.; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Smith, D.J.; Schulte, M.; Bischof, J.B. The Effect of Dimethylsulfoxide on the Water Transport Response of Rat Hepatocytes during Freezing. ASME J. Biomech. Eng. 1998, 120, 549–558. [Google Scholar] [CrossRef]
- Hobbs, P.V. Ice Physics; Clarendon Press: Oxford, UK, 1974; pp. 361–362. [Google Scholar]
- He, X.; Fowler, A.; Toner, M. Water Activity and Mobility in Solutins of Glycerol and Small Molecular Weight Sugars: Implications for Cryo- and Lyopreservation. J. Appl. Phys. 2006, 100, 074702. [Google Scholar] [CrossRef]
- Morris, G.J.; Goodrich, M.; Acton, E.; Fonseca, F. The High Viscosity Encountered During Freezing in Glycerol Solutions: Effects on Cryopreservation. Cryobiology 2006, 52, 323–334. [Google Scholar] [CrossRef]
- Choi, J.; Bischof, J.C. Review of Biomaterial Thermal Property Measurements in the Cryogenic Regime and their use for Prediction of Equilibrium and Non-Equilibrium Freezing Applications in Cryobiology. Cryobiology 2010, 60, 52–70. [Google Scholar] [CrossRef] [Green Version]
- Takamura, K.; Fischer, H.; Morrow, N.R. Physical Properties of Aqueous Glycerol Solutions. J. Pet. Sci. Eng. 2012, 98-99, 50–60. [Google Scholar] [CrossRef]
- Gonzalez, J.A.T.; Longinotti, M.P.; Corti, H.R. Viscosity of Supercooled Aqueous Glycerol Solutions, Validity of the Stokes-Einstein Relationship, and Implications for Cryopreservation. Cryobiology 2012, 65, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Vinson, T.S.; Jahn, S.L. Latent Heat of Frozen Saline Coarse-Grained Soil. J. Geotech. Eng. 1985, 111, 607–623. [Google Scholar] [CrossRef]
- Defay, R.; Sanfield, A. Chaleur de Fusion de la Glace en Présence d’une Solution Aquese de Sel. Bull. Soc. Chim. Belg. 1959, 68, 295–302. [Google Scholar] [CrossRef]
- Taborsky, G. Solute Redistribution in some Multicomponent Aqueous Systems on Freezing. J. Biol. Chem. 1970, 245, 1063–1068. [Google Scholar] [CrossRef]
- Lumry, R.; Rajender, S. Enthalpy-Entropy Compensation Phenomena in Water solution of Proteins and Small Molecules: A Ubiquitous Property of Water. Polymers 1970, 9, 1125–1227. [Google Scholar] [CrossRef]
- Han, B.; Choi, J.-H.; Dantzig, J.A.; Bischof, J.C. A Quantitative Analysis on Latent Heat of an Aqueous Binary Mixture. Cryobiology 2006, 52, 146–151. [Google Scholar] [CrossRef]
- Kumano, H.; Asaoka, T.; Saito, A.; Okawa, S. Study on Latent Heat of Fusion of Ice in Aqueous Solutions. Int. J. Refrig. 2007, 30, 267–273. [Google Scholar] [CrossRef]
- Choi, J.-H.; Bischof, J.C. A Quantitative Analysis of the Thermal Properties of Porcine Liver with Glycerol at Subzero and Cryogenic Temperatures. Cryobiology 2008, 57, 79–83. [Google Scholar] [CrossRef]
- Kumano, H.; Asaoka, T.; Saito, A.; Okawa, S. Formulation of the Latent Heat of Fusion of Ice in Aqueous Solutions. Int. J. Refrig. 2009, 32, 175–182. [Google Scholar] [CrossRef]
- Krishnaswamy, S.; Sahu, P.; Ponnani, K. Calorimetry Based Temperature and Specific Enthalpy Measurements Associated with Ice-Water Phase Change in Saline Systems for Freeze Desalination. Int. J. Thermofluids 2022, 15, 100175. [Google Scholar] [CrossRef]





| Aqueous Solution | Magnitude of DSC-Measured Heat Release (J/g) | % of Dissolved Solids | |
|---|---|---|---|
| Linear Baseline (Tph to ~–40 °C) | Sigmoidal Baseline (Tph to ~–22 °C) | ||
| Pure Water | 335.0 ± 5.0 | 335.0 ± 5.0 | 0.0 |
| PBS: | |||
| 1 × PBS | 302.0 ± 5.0 | 256.0 ± 5.0 | 0.98 ± 0.05 |
| 5 × PBS | 221.0 ± 5.0 | 183.0 ± 5.0 | 5.34 ± 0.07 |
| 10 × PBS | 174.0 ± 5.0 | 142.0 ± 5.0 | 9.81 ± 0.04 |
| Glycerol in 1 × PBS: | |||
| 0.05 moles | 294.0 ± 5.0 | 243.0 ± 5.0 | 0.91 ± 0.04 |
| 0.1 moles | 261.0 ± 5.0 | 221.0 ± 5.0 | 1.18 ± 0.06 |
| 0.5 moles | 213.0 ± 5.0 | 171.0 ± 5.0 | 3.27 ± 0.02 |
| 1.0 moles | 166.0 ± 5.0 | 136.0 ± 5.0 | 7.82 ± 0.07 |
| RPMI: | 261.0 ± 5.0 | 224.0 ± 5.0 | 1.84 ± 0.06 |
| Serum-Free | |||
| Cell Culture Media (20% FBS with 1% penn-strep) | 221.0 ± 5.0 | 184.0 ± 5.0 | 1.78 ± 0.05 |
| Aqueous Solution | Temperature Dependence Parameters | Time Dependence Parameters | ||
|---|---|---|---|---|
| A | Tph (K) | Constant, k | Time Exponent, n | |
| 1 × PBS | 0.53 | 272.62 | 3.3 | 1.5 |
| 10 × PBS | 0.53 | 267.85 | 3.3 | 1.5 |
| 1 M Glycerol in 1 × PBS | 0.53 | 270.75 | 2.3 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, S.; Hall, C.; Das, S.; Devireddy, R. Freezing of Solute-Laden Aqueous Solutions: Kinetics of Crystallization and Heat- and Mass-Transfer-Limited Model. Bioengineering 2022, 9, 540. https://doi.org/10.3390/bioengineering9100540
Johnson S, Hall C, Das S, Devireddy R. Freezing of Solute-Laden Aqueous Solutions: Kinetics of Crystallization and Heat- and Mass-Transfer-Limited Model. Bioengineering. 2022; 9(10):540. https://doi.org/10.3390/bioengineering9100540
Chicago/Turabian StyleJohnson, Stonewall, Christopher Hall, Sreyashi Das, and Ram Devireddy. 2022. "Freezing of Solute-Laden Aqueous Solutions: Kinetics of Crystallization and Heat- and Mass-Transfer-Limited Model" Bioengineering 9, no. 10: 540. https://doi.org/10.3390/bioengineering9100540