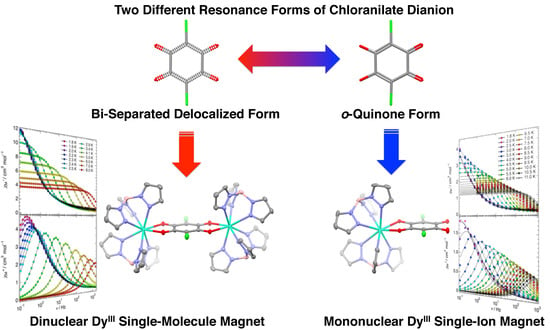
Field-Induced Slow Magnetic Relaxation of Mono- and Dinuclear Dysprosium(III) Complexes Coordinated by a Chloranilate with Different Resonance Forms
Abstract
:1. Introduction
2. Results and Discussion
2.1. Syntheses and Characterizations
2.2. Molecular Structure Descriptions
2.3. Magnetic Properties
2.3.1. Static Magnetic Properties
2.3.2. Dynamic Magnetic Properties
3. Experimental Section
3.1. Materials and Methods
3.2. Synthesis of [{Dy(Tp)2}2(μ-Cl2An)]·2CH2Cl2 (1)
3.3. Synthesis of [{Gd(Tp)2}2(μ-Cl2An)]·2CH2Cl (2)
3.4. Synthesis of [Co(Cp)2][Dy(Tp)2(Cl2An)] (3)
3.5. Single-crystal X-ray Crystallography Data Collection and Refinement
3.6. Physical Measurements
4. Conclusions and Outlook
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Christou, G.; Gatteschi, D.; Hendrickson, D.N.; Sessoli, R. Single-molecule magnets. MRS Bull. 2000, 25, 66–71. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Jeon, I.-R.; Clerac, R. Controlled association of single-molecule magnets (SMMs) into coordination networks: towards a new generation of magnetic materials. Dalton. Trans. 2012, 41, 9569–9586. [Google Scholar] [CrossRef] [PubMed]
- Demir, S.; Jeon, I.-R.; Long, J.R.; Harris, T.D. Radical ligand-containing single-molecule magnets. Coord. Chem. Rev. 2015, 289–290, 149–176. [Google Scholar] [CrossRef]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide single-molecule magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Craig, G.A.; Murrie, M. 3d Single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Pichon, C.; Sutter, J.-P. Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Meng, Y.S.; Jiang, S.D.; Wang, B.W.; Gao, S. Understanding the magnetic anisotropy toward single-ion magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef] [PubMed]
- McAdams, S.G.; Ariciu, A.-M.; Kostopoulos, A.K.; Walsh, J.P.S.; Tuna, F. Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies. Coord. Chem. Rev. 2017, 346, 216–239. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chemie Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef] [PubMed]
- Schlegel, C.; van Slageren, J.; Manoli, M.; Brechin, E.K.; Dressel, M. Direct observation of quantum coherence in single-molecule magnets. Phys. Rev. Lett. 2008, 101, 147203. [Google Scholar] [CrossRef] [PubMed]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D.; Sessoli, R. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179. [Google Scholar] [CrossRef] [PubMed]
- Camarero, J.; Coronado, E. Molecular vs. inorganic spintronics: the role of molecular materials and single molecules. J. Mater. Chem. 2009, 19, 1678–1684. [Google Scholar] [CrossRef]
- Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef] [PubMed]
- Clemente-Juan, J.M.; Coronado, E.; Gaita-Arino, A. Magnetic polyoxometalates: from molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef] [PubMed]
- Sorace, L.; Benelli, C.; Gatteschi, D. Lanthanides in molecular magnetism: old tools in a new field. Chem. Soc. Rev. 2011, 40, 3092–3104. [Google Scholar] [CrossRef] [PubMed]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Kitagawa, S.; Kawata, S. Coordination compounds of 1,4-dihydroxybenzoquinone and its homologues. Structures and properties. Coord. Chem. Rev. 2002, 224, 11–34. [Google Scholar] [CrossRef]
- Mercuri, M.L.; Congiu, F.; Concas, G.; Sahadevan, S.A. Recent advances on anilato-based molecular materials with magnetic and/or conducting properties. Magnetochemistry 2017, 3, 1. [Google Scholar] [CrossRef]
- Trofimenko, S. Recent advances in poly(pyrazolyl)borate (scorpionate) chemistry. Chem. Rev. 1993, 93, 943–980. [Google Scholar] [CrossRef]
- Abdus Subhan, M.; Kawahata, R.; Nakata, H.; Fuyuhiro, A.; Tsukuda, T.; Kaizaki, S. Synthesis, structure and spectroscopic properties of chloranilate-bridged 4f–4f dinuclear complexes: A comparative study of the emission properties with Cr–Ln complexes. Inorganica Chim. Acta 2004, 357, 3139–3146. [Google Scholar] [CrossRef]
- Ishikawa, R.; Horii, Y.; Nakanishi, R.; Ueno, S.; Breedlove, B.K.; Yamashita, M.; Kawata, S. Field-induced single-ion magnetism based on spin-phonon relaxation in a distorted octahedral high-spin cobalt(II) complex. Eur. J. Inorg. Chem. 2016, 2016, 3233–3239. [Google Scholar] [CrossRef]
- Apostolidis, C.; Rebizant, J.; Kanellakopulos, B.; von Ammon, R.; Dornberger, E.; Müller, J.; Powietzka, B.; Nuber, B. Homoscorpionates (hydridotris(1-pyrazolyl)borato complexes) of the trivalent 4f ions. The crystal and molecular structure of [(HB(N2C3H3)3)3LnIII, (Ln = Pr, Nd). Polyhedron 1997, 16, 1057–1068. [Google Scholar] [CrossRef]
- Casanova, D.; Alemany, P.; Bofill, J.M.; Alvarez, S. Shape and symmetry of heptacoordinate transition-metal complexes: Structural trends. Chem. Eur. J. 2003, 9, 1281–1295. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Wernsdorfer, W.; Ungur, L.; Guo, Y.; Tang, J.; Zhang, H.-J.; Chibotaru, L.F.; Powell, A.K. Strong axiality and ising exchange interaction suppress zero-field tunneling of magnetization of an asymmetric Dy2 single-molecule magnet. J. Am. Chem. Soc. 2011, 133, 11948–11951. [Google Scholar] [CrossRef] [PubMed]
- Ungur, L.; Chibotaru, L.F. Magnetic anisotropy in the excited states of low symmetry lanthanide complexes. Phys. Chem. Chem. Phys. 2011, 13, 20086–20090. [Google Scholar] [CrossRef] [PubMed]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Orbach, R. Spin-lattice relaxation in rare-earth salts. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1961, 264, 458–484. [Google Scholar] [CrossRef]
- Orbach, R. On the theory of spin-lattice relaxation in paramagnetic salts. Proc. Phys. Soc. 1961, 77, 821–826. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, UK, 1970. [Google Scholar]
- Shrivastava, K.N. Theory of spin–lattice relaxation. Phys. Status Solidi 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Scott, P.L.; Jeffries, C.D. Spin-lattice relaxation in some rare-earth salts at helium temperatures; observation of the phonon bottleneck. Phys. Rev. 1962, 127, 32–51. [Google Scholar] [CrossRef]
- CrystalClear-SM; Version 1.4.0 SP1; Rigaku and Rigaku/MSC: The Woodlands, TX, USA, 2008.
- CrystalStructure; Version 4.1.1; Rigaku and Rigaku/MSC: The Woodlands, TX, USA, 2015.
- Burla, M.C.; Caliandro, R.; Camalli, M.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Mallamo, M.; Mazzone, A.; Polidori, G.; Spagna, R. SIR2011: A new package for crystal structure determination and refinement. J. Appl. Crystallogr. 2012, 45, 357–361. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Kahn, O. Molecular Magnetism; VCH: Weinheim, Germany, 1993. [Google Scholar]










© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, R.; Michiwaki, S.; Noda, T.; Katoh, K.; Yamashita, M.; Matsubara, K.; Kawata, S. Field-Induced Slow Magnetic Relaxation of Mono- and Dinuclear Dysprosium(III) Complexes Coordinated by a Chloranilate with Different Resonance Forms. Inorganics 2018, 6, 7. https://doi.org/10.3390/inorganics6010007
Ishikawa R, Michiwaki S, Noda T, Katoh K, Yamashita M, Matsubara K, Kawata S. Field-Induced Slow Magnetic Relaxation of Mono- and Dinuclear Dysprosium(III) Complexes Coordinated by a Chloranilate with Different Resonance Forms. Inorganics. 2018; 6(1):7. https://doi.org/10.3390/inorganics6010007
Chicago/Turabian StyleIshikawa, Ryuta, Shoichi Michiwaki, Takeshi Noda, Keiichi Katoh, Masahiro Yamashita, Kouki Matsubara, and Satoshi Kawata. 2018. "Field-Induced Slow Magnetic Relaxation of Mono- and Dinuclear Dysprosium(III) Complexes Coordinated by a Chloranilate with Different Resonance Forms" Inorganics 6, no. 1: 7. https://doi.org/10.3390/inorganics6010007